
- •1,Кинетические характеристики поступательного движения. Нормальное и тангенциальное ускорения. Зависимость кинематических величин от времени.
- •2.Кинематические характеристики вращательного движения твердого тела. Момент инерции. Кинетическая энергия вращательного движения. Теорема Штейнера.
- •3.Момент силы относительно неподвижной точки, неподвижной оси. Уравнение динамики вращательного движения твердого тела.
- •4.Момент импульса относительно неподвижной точки и момент импульса твердого тела.
- •5. Законы сохранения в механике.
- •6. Гармонические колебания и их характеристики. Квазиупругая сила.
- •7. Энергия гармонических колебаний.
- •8. Простейшие колебательные системы. Пружинный, физический и математический маятники.
- •9.Сложение одинаково направленных колебаний.
- •10. Затухающие колебания. Логарифмический декремент затухания.
- •11.Распределение Максвелла. Скорость молекул.
- •12. Барометрическая формула.
- •13. Явление переноса. Диффузия, внутреннее трение, теплопроводность.
- •14. Внутренняя энергия идеального газа. Закон равномерного распределения энергии по степеням свободы.
- •15. Первый закон термодинамики. Работа газа при изменении объема.
- •16.Теплоемкости идеального газа. Закон Майера.
- •17.Адиабатический процесс. Уравнение Пуассона. Работа газа при адиабатическом процессе. Адиабатическая теплоемкость.
- •18.Круговые процессы(циклы). Обратимый и необратимый циклы. Кпд цикла.
- •19. Цикл Карно и его кпд
- •20. Энтропия. Термодинамическое толкование энтропии. Изменение энтропии в обратимых изопроцессах.
- •21.Статистическое толкование энтропии. Макро- и микросостояния системы. Термодинамическая вероятность.
- •22. Напряженность электрического поля. Графическое изображение электрических полей. Принцип суперпозиции. Поле точечного заряда.
- •23. Теорема Гауса для векторов напряженности электрического поля.
- •24. Применение теоремы Гаусса к расчету некоторых электростатических полей в вакууме
- •4. Поле объемно заряженного шара. Шар
- •25. Работа по перемещению заряда в электрическом поле. Циркуляция вектора напряженности. Потенциал. Разность потенциалов.
- •26. Виды диэлектриков. Поляризация диэлектриков.
- •27.Напряженность электрического поля. Графическое изобр электрических полей. Принцип суперпозиции. Поле точечного заряда.
- •§ 89. Электрическое смещение. Теорема Гаусса для электростатического поля в диэлектрике
- •28. Электроемкость проводника. Емкость плоского конденсатора. Параллельное и последовательное соединение конденсаторов.
- •29. Магнитное поле и его характеристики. Закон Био-Савара-Лапласа и его применение (бесконечный ток, конечный ток, круговой ток)
- •30. Циркуляция вектора индукции магнитного поля.
- •31. Закон Ампера. Сила Лоренца. Действие магнитного поля на движущийся заряд.
- •32. Поток вектора индукции. Теорема Гаусса для вектора индукции.
- •33. Работа по перемещению проводника с током и замкнутого контура в магнитном поле.
- •34. Явление индукции. Закон Фарадея.
- •35. Самоиндукция. Индуктивность. Взаимная индукция.
- •36.Атом во внешнем поле. Диа- и парамагнетизм.
- •37. Вектор намагничивания. Магнитное поле в веществе.
- •38. Уравнение Максвелла в интегральной форме.
- •39. Интерференция света. Условная интерференция.
- •40. Опыт наблюдения интерференции (опыт Юнга, плоскости пластин, кольца Ньютона)
- •2. Кольца Ньютона
- •41. Дифракция Френеля. (на отверстии и диске)
- •42.Дифрацкия Фраунгофера (на щели и решетке)
- •43. Естественный и поляризованный свет. Закон Малюса.
- •44. Поляризация при отражении и преломлении. Закон Брюстера.
- •45. Тепловое излучение и его характеристики. Закон Кирхгофа.
- •46. Излучение черного тела. Законы Стефана-Больцмана и Вина.
- •47. Формула Релея-Джонса. Квантовая природа излучения. Формула Планка.
- •48. Фотоэффект. Формула Эйнштейна для фотоэффекта. Виды фотоэлектрического эффекта. Законы внешнего фотоэффекта
- •49. Масса и Импульс фотона. Давление света.
- •50. Эффект Комптона.
- •51. Волны Де-Бройля.
- •52. Соотношение неопределенной Гейзенберга.
- •53. Уравнение Шредингера. Физический смысл ψ-функции.
- •54.Частица в потенциальной яме.
- •55. Атом водорода в квантовой механике. Квантовые числа. Заполнение эл. Оболочек.
- •56. Принцип Паули, спектр атома водорода, атомные спектры, постоянная Ридберга.
- •57. Политропический процесс, уравнение политропы.
- •58. Уравнение Ван-Дер-Ваальса.
- •58. Второе и третье начала термодинамики.
- •59. Сила и плотность тока, сторонние силы эдс источника.
- •60. Расчет полей соленоида и тороида.
- •62. Энергия системы зарядов. Энергия заряженного проводника. Энергия электрического поля. Объемная плотность энергии.
- •— Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор
- •63. Волновой процесс и его характеристики. Ур-е бегущей волны.
- •64. Электромагнитные волны.
11.Распределение Максвелла. Скорость молекул.
Распределение молекул газа по скоростям (закон Максвелла)
В
результате теплового движения молекул
в газе, находящемся в состоянии теплового
равновесия, устанавливается некоторое
стационарное (постоянное) распределение
молекул по скоростям.
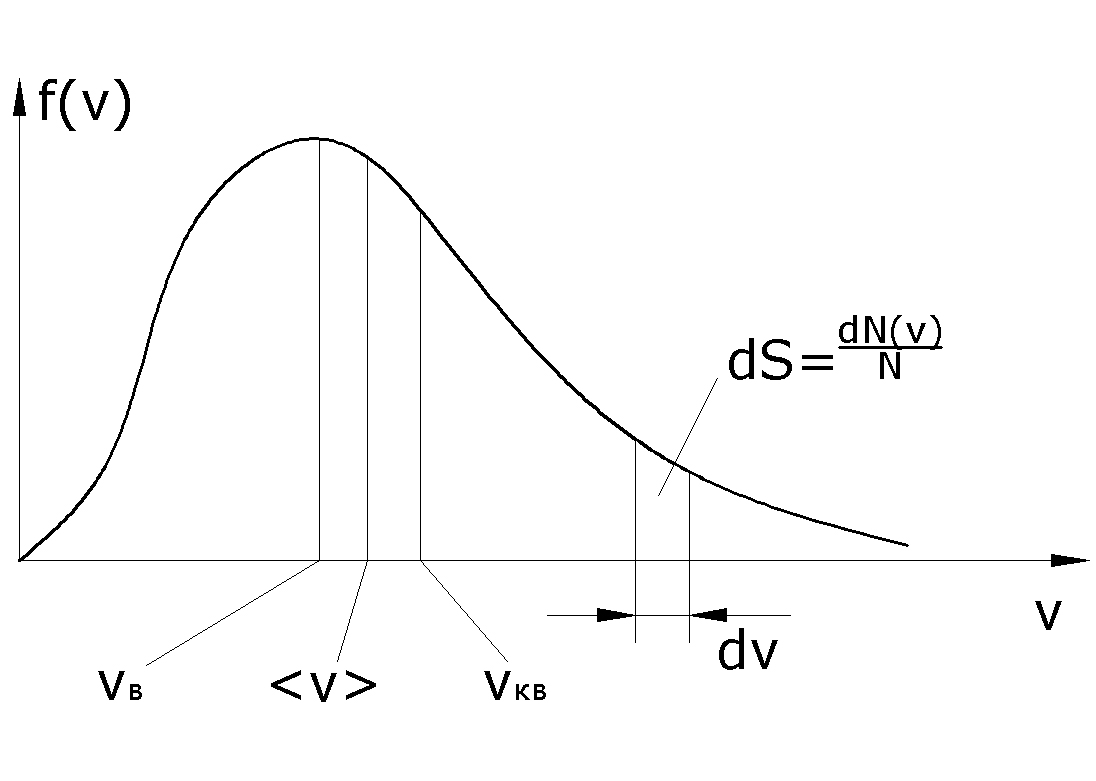 Рис. 5.2
Рис. 5.2
Если
отложить на оси ординат функцию
распределения
 ,
а на оси абсцисс скорости молекул
,
а на оси абсцисс скорости молекул
 ,
и разбить диапазон изменения скоростей
молекул
на малые интервалы
,
и разбить диапазон изменения скоростей
молекул
на малые интервалы
 ,
то на каждый интервал
будет приходиться некоторое количество
молекул
,
то на каждый интервал
будет приходиться некоторое количество
молекул
 ,
имеющих скорость, заключенную в данном
интервале
,
имеющих скорость, заключенную в данном
интервале
(рис. 5.2).
Функция
распределения Максвелла
определяет относительное количество
молекул
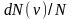 ,
,
скорости
которых заключены в интервале от v
до
 ,
т. е.
,
т. е.
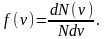 (5.17)
(5.17)
Таким
образом, площадь
 на рис. 5.2 определяет относительное
количество молекул, скорости которых
лежат в интервале от v
до
.
на рис. 5.2 определяет относительное
количество молекул, скорости которых
лежат в интервале от v
до
.
Вид функции распределения молекул по скоростям ,
с использованием теории вероятностей был установлен Максвеллом
 (5.18)
(5.18)
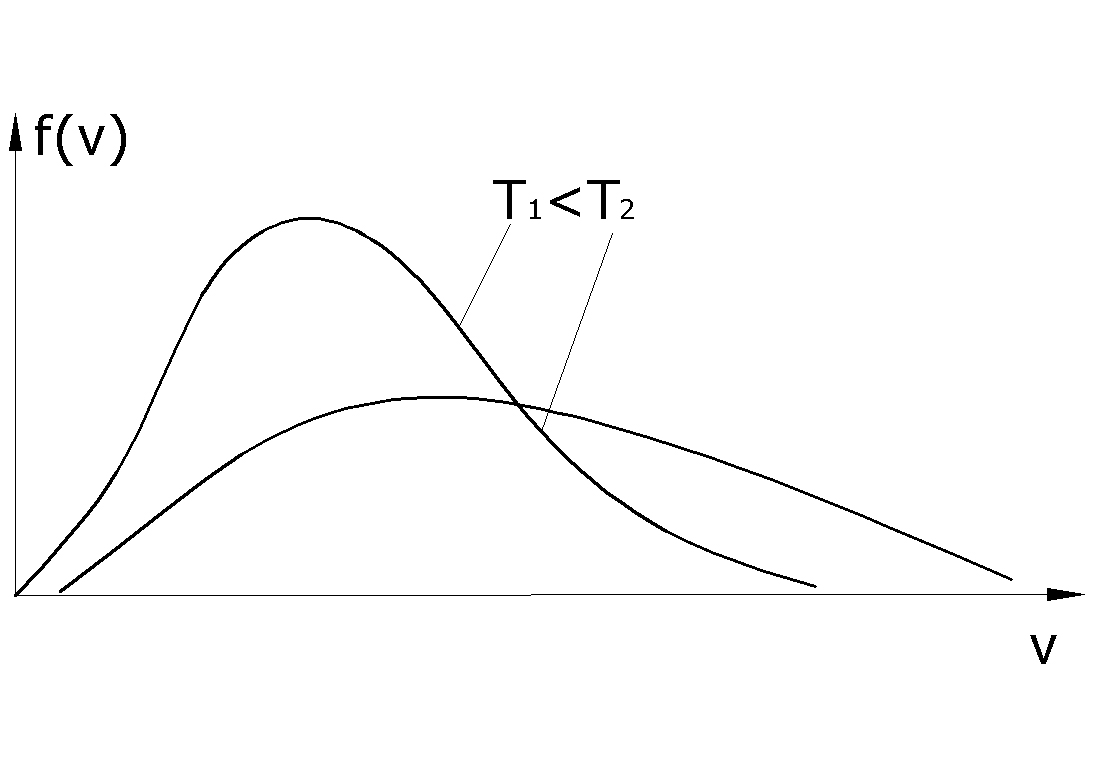
Конкретный вид функции зависит от массы молекул и температуры газа. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице, т. е. функция распределения удовлетворяет условиям нормировки
 (5.19)
(5.19)
а это есть численное значение площади под кривой.
Скорость,
при которой функция распределения
имеет максимум, называется наиболее
вероятной скоростью. Значение
 можно вычислить, приравняв производную
можно вычислить, приравняв производную


 (5.20)
(5.20)
Скорость, определяемая выражением (5.20), имеет наибольшее число молекул.
В
МКТ пользуются также понятием
среднеарифметической скорости
 ,
которая также вычисляется из закона
распределения Максвелла
,
которая также вычисляется из закона
распределения Максвелла
 (5.21)
(5.21)
Напомним, что выражение для среднеквадратичной скорости имеет вид
 (5.22)
(5.22)
12. Барометрическая формула.
Выведем закон изменения давления с высотой, предполагая, что газ находится в поле тяготения Земли.
Предположим,
что это поле однородно, температура
постоянна и масса всех молекул одинакова
и равна
 .
.
Гравитационное
поле, с одной стороны, и тепловое движение
– с другой, приводит к стационарному
распределению молекул газа по высоте,
при котором давление с высотой убывает.
 Рис. 5.4
Пусть на высоте
Рис. 5.4
Пусть на высоте
 давление равно
давление равно
 ,
а на высоте
,
а на высоте
 соответственно
соответственно
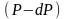 ,
причем, если
,
причем, если
 ,
так как давление с высотой убывает.
,
так как давление с высотой убывает.
По закону Паскаля
 (5.23)
(5.23)
где
 – плотность газа на высоте h
(при малом изменении
– плотность газа на высоте h
(при малом изменении
 ).
).
а
 (5.24)
(5.24)
Вычтя из (5.24) (5.23), получим
 .
(5.25)
.
(5.25)
Используя
уравнение Клапейрона – Менделеева
 ,
выразим плотность газа в виде
,
выразим плотность газа в виде
 (5.26)
(5.26)
Подставив выражение (5.26) в (5.25), получим
 (5.27)
(5.27)
Разделим переменные, формула (5.27) примет вид
 (5.28)
(5.28)
Проинтегрируем (5.28),

получим
 (5.29)
(5.29)
или
 (5.30)
(5.30)
Считаем
давление на уровне моря равным
 ,
тогда выражение (5.30) примет вид
,
тогда выражение (5.30) примет вид
 (5.31)
(5.31)
Выражение (5.31) называется барометрической формулой.
Если
воспользоваться соотношением (4.10)
 получим
получим
 .
(5.32)
.
(5.32)
Учитывая,
что
 – потенциальная энергия молекулы в
поле тяготения, формулу (5.32) можно
представить как
– потенциальная энергия молекулы в
поле тяготения, формулу (5.32) можно
представить как
 (5.33)
(5.33)
Выражение (5.33) называется распределением Больцмана во внешнем потенциальном поле.
Таким
образом, рассмотренные статистические
распределения имеют экспоненциальный
характер, причем в показателе экспоненты
стоит взятое со знаком минус отношение
характерной энергии молекулы к величине
 ,
которая пропорциональна средней
кинетической энергии теплового движения
молекул.
,
которая пропорциональна средней
кинетической энергии теплового движения
молекул.
