6. Гармонические колебания и их характеристики. Квазиупругая сила.

Гармоническое колебание изображают графически методом вращающегося вектора амплитуды (рис. 4.1).

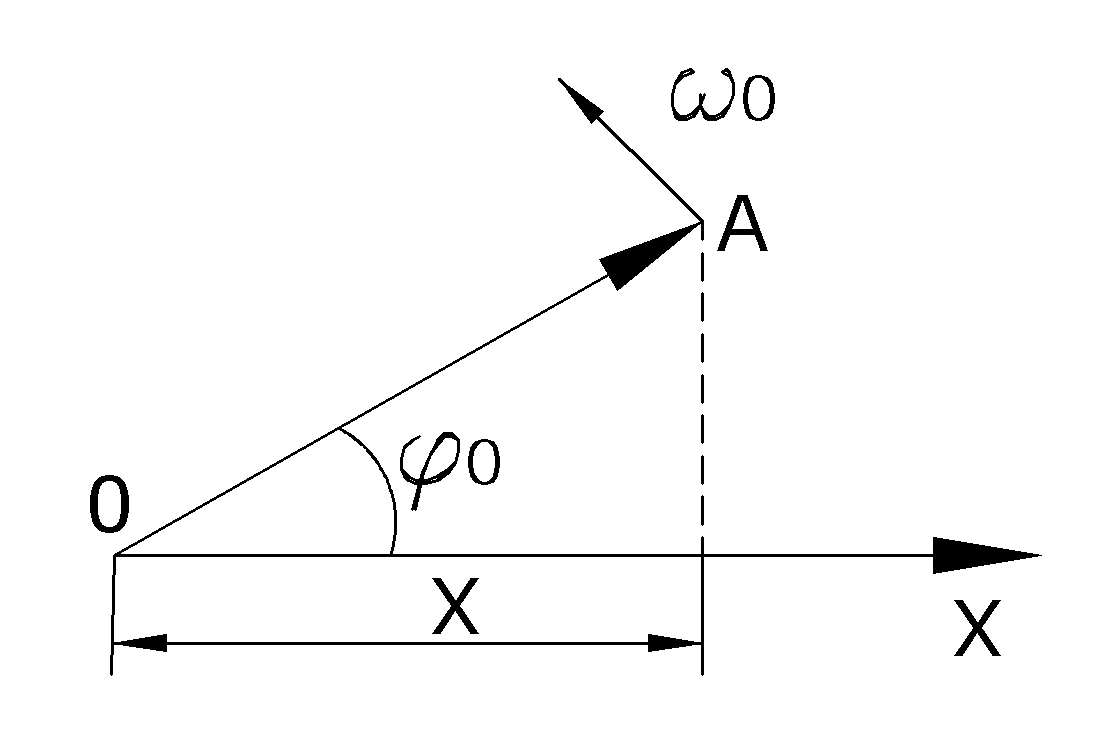
Рис. 4.1

будет изменяться по закону

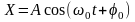(4.1)

где А – амплитуда колебаний; – циклическая частота; 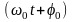– фаза колебаний; – начальная фаза.

Гармонические колебания характеризуют следующие величины:

– период колебаний, время одного полного колебания;

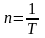– частота колебаний определяет число колебаний, которое совершает система в единицу времени;

– циклическая частота.

Запишем дифференциальное уравнение гармонических колебаний. Для этого найдем первую и вторую производные от (4.1), которые определяют скорость и ускорение при колебательном движении

(4.2)

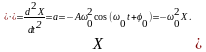(4.3)

Амплитудные значения скорости и ускорения соответственно равны 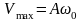и . Фаза скорости отличается от фазы смещения на /2 (рис. 4.2).

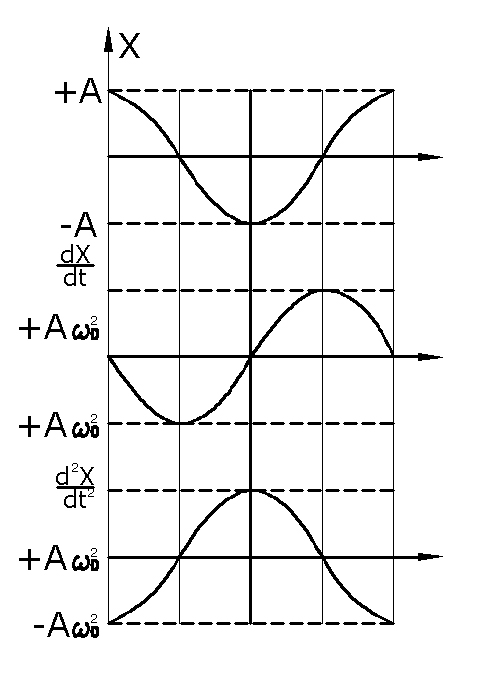
Рис. 4.2

Колебательное движение есть движение с ускорением, поэтому на колеблющееся тело должна действовать сила, сообщающая ему ускорение. Гармонические колебания происходят под действием упругой или квазиупругой силы, которая выражается как: 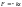. По второму закону Ньютона можно записать

(4.5)

где 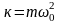– коэффициент пропорциональности.

Квазиупругая сила.

Известно, сила упругости Fупр растянутой (сжатой) пружиныравна по закону Гука: Fупр= -kX, где k – жесткость пружины и X – смещение пружины относительно нерастянутого состояния. Сила F = ma,действующая на колеблющуюся материальную точку массы m, с учетом второго соотношения (2.2) может быть записана в виде

F = mAwo²cos(wot + a) =-m wo²X=-kX,

если обозначить k = m wo². Эта сила, не являясь по своей природе упругой, по форме совпадает с Fупр. Сила F = -m wo²X, действующая на колеблющуюся точку, пропорциональна смещению точки из положения равновесия, направлена в противоположную смещению сторону и называется квазиупругой силой.

7. Энергия гармонических колебаний.

Кинетическую энергию гармонических колебаний можно представить в виде

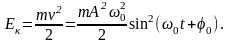(4.6)

Потенциальная энергия гармонического колебания под действием квазиупругой силы F = – кХ определяется в виде

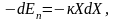
(4.7)

Полную энергию представляем как сумму выражений (4.6) и (4.7) и равную

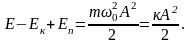(4.8)

Таким образом, если пренебречь силами трения, то полная энергия колеблющейся системы остается постоянной величиной.

8. Простейшие колебательные системы. Пружинный, физический и математический маятники.

Колеблющаяся система, описываемая уравнением

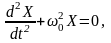(4.9)

называется гармоническим осциллятором.

Гармонический осциллятор служит точной или приближенной моделью во многих задачах классической и квантовой физики.

Примерами гармонического осциллятора в механике служат пружинный, физический и математический маятники.

Пружинный маятник. Груз массой m, прикрепленный к абсолютно упругой пружине с коэффициентом жесткости (упругости) к, совершает колебания под действием квазиупругой силы

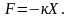
Уравнение движения имеет вид

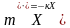
или

(4.10)

Решением уравнения является выражение

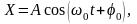(4.11)

Где

и – собственная частота колебаний маятника;

– период колебаний пружинного маятника.

Физический маятник, показанный на рис. 4.3, представляет собой твердое тело, совершающее под действием силы тяжести малые колебания вокруг горизонтальной неподвижной оси (точка О), не проходящей через центр массы тела (точка С).

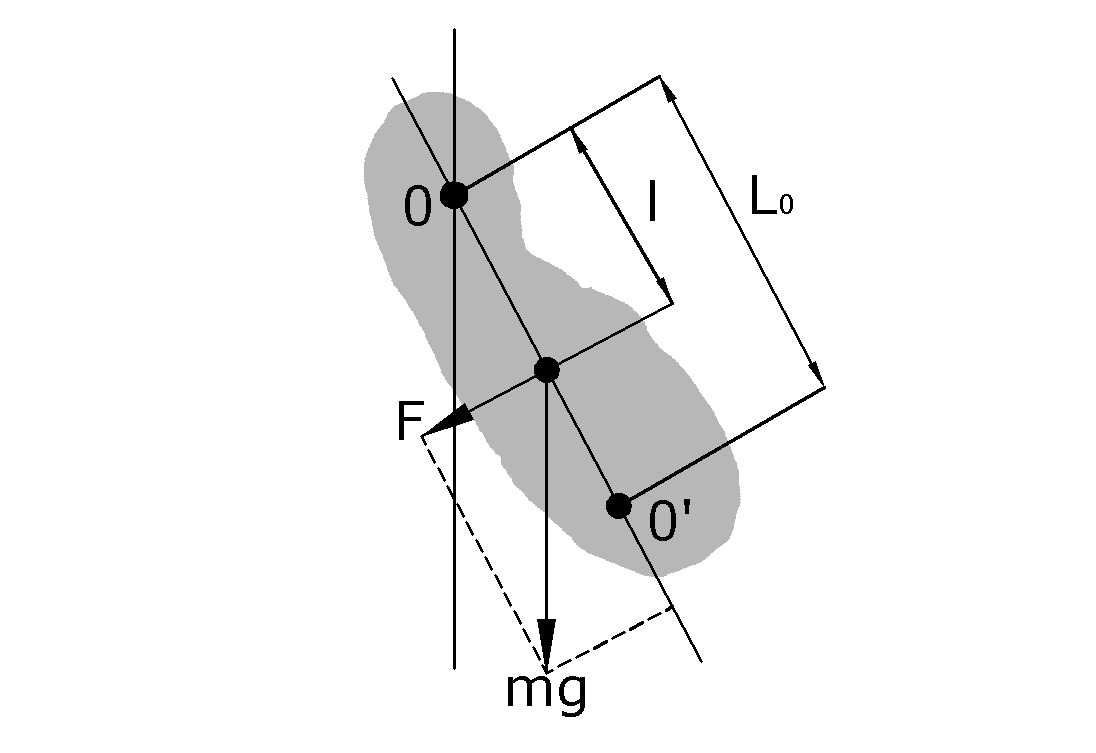
Рис. 4.3

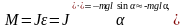(4.12)

так как для малых углов

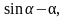
где l – расстояние между точкой подвеса О и центром масс маятника; – момент инерции относительно оси, проходящей через точку О; ( )– момент возвращающей силы, т. е. произведение силы тяжести на плечо.

Перепишем уравнение (4.12) в виде

или

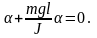(4.13)

Обозначив

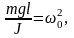
получим

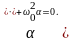(4.14)

Решение уравнения (4.14) имеет вид

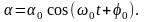(4.15)

Таким образом, при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω₀ и периодом, равным

(4.16)

Математический маятник – идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой и невесомой нити длиной l, и колеблющаяся под действием силы тяжести.

Момент инерции математического маятника определяется как

(4.17)

Математический маятник можно рассматривать как частный случай физического маятника, предположив, что вся масса физического маятника сосредоточена в центре масс.

Тогда, подставив в (4.16) выражение для момента инерции, получим период колебаний математического маятника в виде

(4.18)