3.Момент силы относительно неподвижной точки, неподвижной оси. Уравнение динамики вращательного движения твердого тела.

. Момент силы. Уравнение динамики вращательного движения твердого тела

Моментом силы F относительно неподвиж­ной точки О называется физическая вели­чина, определяемая векторным произведе­нием радиуса-вектора г, проведенного из точки О в точку А приложения силы, на силу F (рис. 25):

M = [rF].

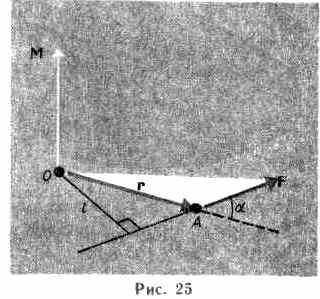
Здесь М — псевдовектор, его направление совпадает с направлением поступательно­го движения правого винта при его враще­нии от г к F.

Модуль момента силы

M = Frsin= Fl, (18.1)

где  — угол между г и F; rsin =l — кратчайшее расстояние между линией дей­ствия силы и точкой О — плечо силы.Моментом силы относительно непод­вижной оси z называется скалярная вели­чина М_z, равная проекции на эту ось век­тор а М момента силы, определенного от­носительно произвольной точки О данной оси 2 (рис.26). Значение момента М_z не зависит от выбора положения точки О на оси z.

Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:

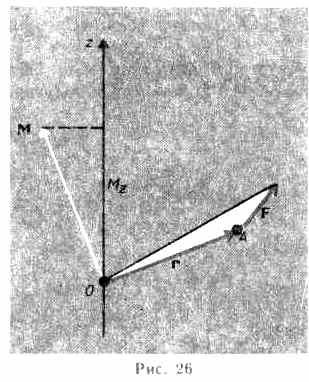
М_z = [rF]_z.

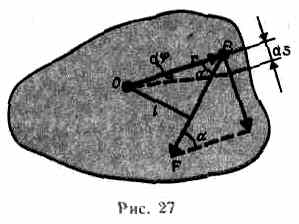
Найдем выражение для работы при вращении тела (рис.27). Пусть сила F приложена в точке В, находящейся от оси вращения на расстоянии r,  — угол между направлением силы и радиусом-вектором r. Так как тело абсолютно твер­дое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол d точка приложения В проходит путь ds= rd, и работа равна произведению проекции силы на направление смещения на величину смещения:

dA=Fsinrd. (18.2) Учитывая (18.1), можем записать dA=M_zd,

где Frsin = Fl =M_z — момент силы от­носительно оси z. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол пово­рота.

Р абота при вращении тела идет на увеличение его кинетической энергии:

dA = dT, но

Учитывая, что =d/dt, получим

Уравнение (18.3) представляет собой уравнение динамики вращательного дви­жения твердого тела относительно непод­вижной оси.

Можно показать, что если ось враще­ния совпадает с главной осью инерции (см. §20), проходящей через центр масс, то имеет место векторное равенство

где J — главный момент инерции тела (момент инерции относительно главной оси).

4.Момент импульса относительно неподвижной точки и момент импульса твердого тела.

М оментом импульса отдельной частицы, имеющей массу m_i , относительно некоторой точки О называется вектор равный векторному произведению радиуса-вектора точки на ее импульс:

(3.17)

где – угол между векторами и .

Моментом импульса твердого тела относительно некоторой точки О называется вектор, равный геометрической сумме моментов импульса относительно той же точки всех частиц системы

(3.18)

Моментом импульса твердого тела относительно некоторой оси называется проекция на эту ось вектора момента импульса системы

(3.19)

Учитывая, что , выражение (3.18) можно записать в виде

(3.20)

Таким образом, момент импульса твердого тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость

(3.21)

Дифференцируя выражение (3.20) по времени, получим

(3.22)

Д ля изолированной системы момент внешних сил равен нулю , тогда или , т. е.

выполняется закон сохранения момента импульса

(3.23)

Из (3.22) следует, что момент импульса относительно оси вращения изолированной системы сохраняется.