29. Магнитное поле и его характеристики. Закон Био-Савара-Лапласа и его применение (бесконечный ток, конечный ток, круговой ток)

Магнитное поле и его характеристики. При прохождении электрического тока по проводнику вокруг него образуется магнитное поле. Магнитное поле представляет собой один из видов материи. Оно обладает энергией, которая проявляет себя в виде электромагнитных сил, действующих на отдельные движущиеся электрические заряды (электроны и ионы) и на их потоки, т. е. электрический ток. Под влиянием электромагнитных сил движущиеся заряженные частицы отклоняются от своего первоначального пути в направлении, перпендикулярном полю (рис. 34).Магнитное поле образуется только вокруг движущихся электрических зарядов, и его действие распространяется тоже лишь на движущиеся заряды. Магнитное и электрические поля неразрывны и образуют совместно единое электромагнитное поле. Всякое изменение электрического поляприводит к появлению магнитного поля и, наоборот, всякое изменение магнитного поля сопровождается возникновением электрического поля. Электромагнитное поле распространяется со скоростью света, т. е. 300 000 км/с.

Графическое изображение магнитного поля. Графически магнитное поле изображают магнитными силовыми линиями, которые проводят так, чтобы направление силовой линии в каждой точке поля совпадало с направлением сил поля; магнитные силовые линии всегда являются непрерывными и замкнутыми. Направление магнитного поля в каждой точке может быть определено при помощи магнитной стрелки. Северный полюс стрелки всегда устанавливается в направлении действия сил поля. Конец постоянного магнита, из которого выходят силовые линии (рис. 35, а), принято считать северным полюсом, а противоположный конец, в который входят силовые линии,— южным полюсом (силовые линии, проходящие внутри магнита, не показаны). Распределение силовых линий между полюсами плоского магнита можно обнаружить при помощи стальных опилок, насыпанных на лист бумаги, положенный на полюсы (рис. 35, б). Для магнитного поля в воздушном зазоре между двумя параллельно расположенными разноименными полюсами постоянного магнита характерно равномерное распределение силовых магнитных линий (рис. 36) (силовые линии, проходящие внутри магнита, не показаны).

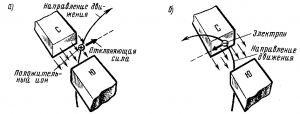Рис. 34. Схемы действия магнитного поля на движущиеся электрические заряды: положительный ион (а) и электрон (б).

Рис. 35. Магнитное поле, созданное постоянным магнитом.

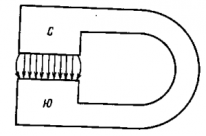
Рис. 36. Однородное магнитное поле между полюсами постоянного магнита.

Рис. 37. Магнитный поток, пронизывающий катушку при перпендикулярном (а) и наклонном (б) ее положениях по отношению к направлению магнитных силовых линий.

Для более наглядного изображения магнитного поля силовые линии располагают реже или гуще. В тех местах, где магнитное роле сильнее, силовые линии располагают ближе друг к другу, там же, где оно слабее,— дальше друг от друга. Силовые линии нигде не пересекаются.

Во многих случаях удобно рассматривать магнитные силовые линии как некоторые упругие растянутые нити, которые стремятся сократиться, а также взаимно отталкиваются друг от друга (имеют взаимный боковой распор). Такое механическое представление о силовых линиях позволяет наглядно объяснить возникновение электромагнитных сил при взаимодействии магнитного поля и Проводника с током, а также двух магнитных полей.

Основными характеристиками магнитного поля являются магнитная индукция, магнитный поток, магнитная проницаемость и напряженность магнитного поля.

Магнитное поле постоянных токов различ­ной формы изучалось французскими уче­ными Ж. Био (1774—1862) и Ф. Саваром (1791 —1841). Результаты этих опытов бы­ли обобщены выдающимся французским математиком и физиком П. Лапласом.

Закон Био — Савара — Лапласа для проводника с током I, элемент которого dlсоздает в некоторой точкеА(рис. 164) индукцию поля dB, записывается в виде где dl— вектор, по модулю равный длине dlэлемента проводника и совпадающий по направлению с током, r — радиус-вектор,

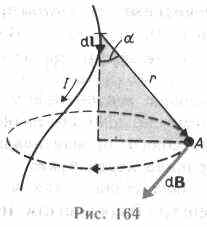
проведенный из элемента dlпроводника в точкуАполя, r— модуль радиуса-векто­ра г. Направление dBперпендикулярно dlи r, т. е. перпендикулярно плоскости, в ко­торой они лежат, и совпадает с каса­тельной к линии магнитной индукции. Это направление может быть найдено по пра­вилу нахождения линий магнитной индук­ции (правилу правого винта): направле­ние вращения головки винта дает направ­ление dB, если поступательное движение винта соответствует направлению тока в элементе.

Модуль вектора dBопределяется вы­ражением

где а — угол между векторами dlи г.

Для магнитного поля, как и для элек­трического, справедлив принцип суперпо­зиции: магнитная индукция результирую­щего поля, создаваемого несколькими то­ками или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каж­дым током или движущимся зарядом в от­дельности:

Расчет характеристик магнитного поля (В и Н) по приведенным формулам в об­щем случае довольно сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био — Савара — Лапласа совместно с принци­пом суперпозиции позволяет довольно просто рассчитать конкретные поля. Рас­смотрим два примера.

1. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165).

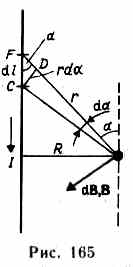
В произвольной точкеА, удаленной от оси проводника на расстояние R, векторы dBот всех элементов тока имеют одина­ковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов dBможно заменить сложением их модулей. В качестве по­стоянной интегрирования выберем угол а (угол между векторами dlи r), выразив через него все остальные величины. Из рис. 165 следует, что

(радиус дуги CDвследствие малости dlравен r, и угол FDCпо этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что маг­нитная индукция, создаваемая одним эле­ментом проводника, равна

Так как угол а для всех элементов прямо­го тока изменяется в пределах от 0 до я, то, согласно (110.3) и (110.4), Следовательно, магнитная индукция поля прямого тока

2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следу­ет из рисунка, все элементы кругового проводника с током создают в центре магнитное поле одинакового направления — вдоль нормали от витка.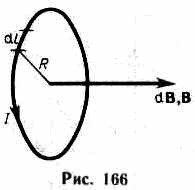

Поэтому сложе­ние векторов dBможно заменить сложени­ем их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору(sin=1) и расстояние всех эле­ментов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2)

,

Тогда

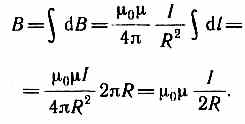
Следовательно, магнитная индукция поля в центре кругового проводника с током