1,Кинетические характеристики поступательного движения. Нормальное и тангенциальное ускорения. Зависимость кинематических величин от времени.

Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин, его вызывающих.

В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда.

Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Так можно поступать, например, при изучении движения планет вокруг Солнца.

Если все части тела движутся одинаково, то такое движение называется поступательным. Поступательно движутся, например, кабины в аттракционе «Колесо обозрения», автомобиль на прямолинейном участке пути и т. д. При поступательном движении тела его также можно рассматривать как материальную точку.

Тело, размерами которого в данных условиях можно пренебречь, называется  материальной точкой.

Понятие материальной точки играет важную роль в механике.

Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.

Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени x = x (t), y = y (t), z = z (t) (координатный способ), либо при помощи зависимости от времени радиус-вектора

   

(векторный способ), проведенного из начала координат до данной точки (рис. 1.1.1). Рисунок 1.1.1.

Определение положения точки с помощью координат x = x (t),y = y (t) и z = z (t) и радиус-вектора 

.   

– радиус-вектор положения точки в начальный момент времени

П еремещением тела  

называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.

Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. 

Путь – скалярная величина.

Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути.

В случае достаточно малого промежутка времени Δt пройденный телом путь Δl почти совпадает с модулем вектора перемещения

   

При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути

Д ля характеристики движения вводится понятие средней скорости: 

В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени Δt: 

В математике такой предел называют производной и обозначают

   или 

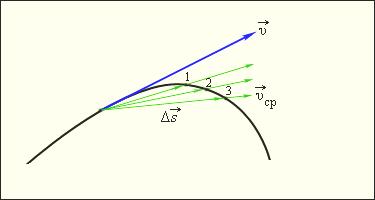
М гновенная скорость   тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.

П ри движении тела по криволинейной траектории его скорость  изменяется по модулю и направлению. Изменение вектора скорости  за некоторый малый промежуток времени Δt можно задать с помощью вектора

 Вектор изменения скорости

  за малое время Δt можно разложить на две составляющие:

  

направленную вдоль вектора (касательная составляющая),

и направленную перпендикулярно вектору  (нормальная составляющая).

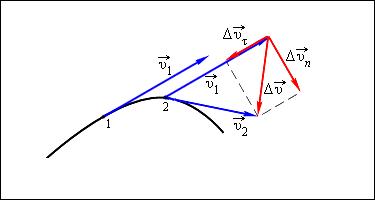
Рисунок 1.1.4.

И зменение вектора скорости по величине и направлению.

    – изменение вектора скорости за время 

Мгновенным ускорением (или просто ускорением) 

т ела называют предел отношения малого изменения скорости

   к малому промежутку времени Δt, в течение которого происходило изменение скорости: 

Н аправление вектора ускорения   в случае криволинейного движения не совпадает с направлением вектора скорости

   Составляющие вектора ускорения  называют касательным (тангенциальным)

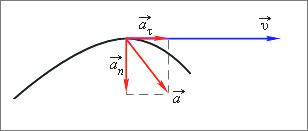   инормальным   ускорениями (рис. 1.1.5).

К асательное ускорение указывает, насколько быстро изменяется скорость тела по модулю:

Вектор  направлен по касательной к траектории.

Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению.

Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).

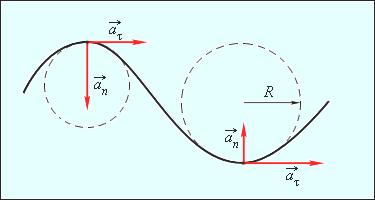
Н ормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент: 

Вектор  всегда направлен к центру окружности

И з рис. 1.1.5 видно, что модуль полного ускорения равен

 

Т аким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение , Скорость и ускорение

Путь l является скалярной величиной.

Перемещение , скорость  и ускорение  – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д. Полное ускорение тела есть геометри­ческая сумма тангенциальной и нормаль­ной составляющих (рис.5):

Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения — быстроту из­менения скорости по направлению (на­правлена к центру кривизны траекто­рии).

В зависимости от тангенциальной и нормальной составляющих ускорения дви­жение можно классифицировать следую­щим образом:

1) а_=0, а_n = 0 — прямолинейное рав­номерное движение;

2) a_=a=const, a_n=0 — прямолиней­ное равнопеременное движение.

При та­ком виде движения

Если начальный момент времени t₁=0, а начальная скорость v₁=v₀, то, обозна­чив t₂ = t и v₂ = v, получим a = (v-v₀)/t, откуда v =v₀+at.

П роинтегрировав эту формулу в пре­делах от нуля до произвольного момента времени t, найдем, что длина пути, прой­денного точкой, в случае равнопеременно­го движения

3) а_=f(t), а_n=0 — прямолинейное движение с переменным ускорением;

4) а_=0, а_n=const. При а_=0 ско­рость по модулю не изменяется, а изменя­ется по направлению. Из формулы а_n= v²/r следует, что радиус кривизны до­лжен быть постоянным. Следовательно, движение по окружности является равно­мерным;

5) а_=0, а_n0 — равномерное кри­волинейное движение;

6) a_=const, a_n0—криволинейное равнопеременное движение

7) a_= f(t), a_n0 — криволинейное движение с переменным ускорением.

Зависимость кинематических характеристик от времени

П ри движении материальной точки A ее координаты и, следовательно, радиус-вектор изменяются с течением времени. В прямоугольной системе координат траектория движения материальной точки определяется тремя скалярными уравнениями:

к оторые эквивалентны векторному уравнению

где – единичные орты координатных осей.

Д лина участка траектории АВ, пройденного материальной точкой за время t, называется длиной пути s и является скалярной функцией времени