
- •Вопрос 9. Цилиндрические прямозубые передачи. Устройство и основные геометрические соотношения
- •Передач с эвольвентным профилем зубьев
- •Вопрос 10. Расчет зубьев цилиндрической прямозубой передачи на изгиб
- •Р ис. 34. Усилия в зацеплении прямозубой цилиндрической передачи
- •Вопрос 11-12. Расчет цилиндрической прямозубой передачи на контактную прочность
- •Вопрос 13. Особенности расчета открытых
- •Вопрос14. Косозубые цилиндрические передачи. Особые размерные параметры….
- •1.1 Общие сведения.
- •1.2 Эквивалентное колесо
- •1.3. Силы в зацеплении
- •Вопрос 16. Расчет косозубых цилиндрических передач.
- •1.5. Расчет на изгиб
- •Вопрос 17. Шевронные передачи.
- •Вопрос 21 червячные передачи
- •Вопрос 22кпд червячной передачи, так же, как зубчатой, определяют по формуле ;
- •Вопрос 23
- •Вопрос 24
- •Вопрос 25
- •Вопрос 26
- •Вопрос 27
- •30)Клиноремённая передача
- •33)Валы и оси
- •35) Проверка валов на статическую прочность
- •36) Подшипники
- •39) Подшипники качения
- •40) Выбор подшипников по динамической грузоподъёмности с (по заданному ресурсу или долговечности)
- •42) Проверка и подбор подшипников по статической грузоподъёмности
- •43) Муфты
- •46) Муфты упругие
- •49. Соединения деталей
Вопрос 22кпд червячной передачи, так же, как зубчатой, определяют по формуле ;
так
как червячная передача подобна винтовой,
её КПД при ведущем червяке можно записать
следующей формулой: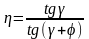 где:
- угол подъёма винтовой линии червяка;
- угол трения (
= arctgf;
f
– коэффициент трения).
где:
- угол подъёма винтовой линии червяка;
- угол трения (
= arctgf;
f
– коэффициент трения).
КПД увеличивается с увеличением числа заходов червяка z1 (увеличивается ) и с уменьшением коэффициента трения.Если ведущим является колесо, то вследствие изменения направления сил, получаем для КПД формулу
 .При
,
= 0 передача движения в обратном направлении
(от колеса к червяку) становится
невозможной. Получаем
самотормозящуюся червячную пару.Для
предварительных расчётов КПД червячной
пары 0,7…0,92.
.При
,
= 0 передача движения в обратном направлении
(от колеса к червяку) становится
невозможной. Получаем
самотормозящуюся червячную пару.Для
предварительных расчётов КПД червячной
пары 0,7…0,92.
Кинематические параметры
Передаточное
отношение.
В червячной передаче в отличие от
зубчатой окружные скорости v1
и v2
не совпадают. Они направлены под углом
90
и различны по значению. Поэтому червячная
передача имеет следующие особенности:
передаточное отношение не может быть
выражено отношением d2/d1,
так как в относительном движении
начальные цилиндры не обкатываются, а
скользят. При одном обороте червяка
колесо повернётся на угол, охватывающий
число зубьев колеса, равное числу заходов
червяка. Для полного оборота колеса
необходимо z2/z1
оборотов червяка, то есть
 .
.
Число заходов червяка выполняет здесь функцию числа зубьев шестерни в зубчатой передаче. Так как z1 может быть небольшим и часто равным единице (чего не может быть у шестерни), то в одной червячной паре можно получить большое передаточное отношение. Это и является основным достоинством червячных передач.
В силовых передачах наиболее распространеныi =10…60; в кинематических передачах встречаются i до 300 и более.
Скольжение
в зацеплении. При движении витки червяка
скользят по зубьям колеса, как в винтовой
паре. Скорость скольжения vs
направлена по касательной к винтовой
линии червяка. Как относительная
скорость, она равна геометрической
разности абсолютных скоростей червяка
и колеса, которыми в данном случае
являются окружные скорости v1
и v2: ;
;
 И,
далее,
И,
далее,
 ;
; ;
;
 ;
;
 .Здесь
- угол подъёма винтовой линии червяка.
Так как практически 30
,
то в червячной передаче v2
всегда значительно меньше v1,
а vs
больше v1.Большое
скольжение в червячных передачах служит
причиной пониженного КПД, повышенного
износа и склонности к заеданию (основные
недостатки червячных передач).
.Здесь
- угол подъёма винтовой линии червяка.
Так как практически 30
,
то в червячной передаче v2
всегда значительно меньше v1,
а vs
больше v1.Большое
скольжение в червячных передачах служит
причиной пониженного КПД, повышенного
износа и склонности к заеданию (основные
недостатки червячных передач).
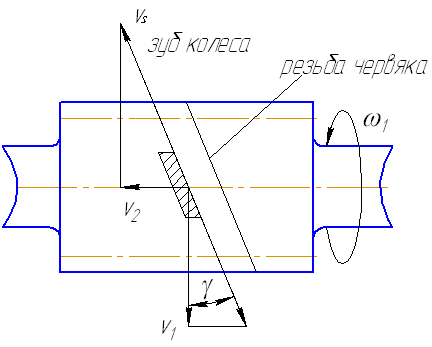
Силы в зацеплении
В
червячном зацеплении действуют: окружная
сила Ft1,
Ft2,
радиальная сила, Fr1,
Fr2,
осевая сила Fa1,
Fa2.
Они равны ;
;
 ;Fr1
= Fr2
= Ft2tg.Нормальная
сила
;Fr1
= Fr2
= Ft2tg.Нормальная
сила

Эти формулы получены на основании рисунка, на котором изображено осевое сечение витка червяка.
Вопрос 23
Основные критерии работоспособности и расчёта
Червячные передачи, так же как и зубчатые, рассчитывают по напряжениям изгиба и контактным напряжениям. В отличие от зубчатых в червячных передачах чаще наблюдается износ и заедание, а не выкрашивание поверхности зубьев. При «мягком» материале колеса (оловянистые бронзы) заедание проявляется в постепенном «намазывании» бронзы начервяк, при котором передача может ещё работать продолжительное время. При твёрдых материалах (алюминиево-железестые бронзы, чугуны) заедание переходит в задир поверхности зубьев с последующим быстрым разрушением.Повышенный износ и заедание червячных передач связаны с большими скоростями скольжения и неблагоприятным направлением скольжения относительно линии контактов.Для предупреждения заедания ограничивают значения контактных напряжений и применяют специальные антифрикционные пары материалов: червяк-сталь, колесо-бронза или чугун. Устранение заедания в червячных передачах не устраняет абразивного износа зубьев. Интенсивность износа зависит также от значения контактных напряжений. Поэтому расчёт по контактным напряжениям для червячных передач является основным. Расчёт по напряжениям изгиба производится при этом как проверочный.
Расчёт на прочность по контактным напряжениям
Проверочный расчёт на прочность по контактным напряжениям выполняется по формуле
 ,
МПа (11)где: d1,
d2
– делительные диаметры червяка и
колеса;N1
– мощность на валу червяка;n2
– частота вращения колеса;КН
– коэффициент расчётной нагрузки;
- КПД червячной пары. Для
проверочного расчёта
формула (11) решается относительно модуля
передачи. Диаметры d1
и d2
равны:
,
МПа (11)где: d1,
d2
– делительные диаметры червяка и
колеса;N1
– мощность на валу червяка;n2
– частота вращения колеса;КН
– коэффициент расчётной нагрузки;
- КПД червячной пары. Для
проверочного расчёта
формула (11) решается относительно модуля
передачи. Диаметры d1
и d2
равны:
 ;
;
 тогда
тогда
 ,
мм (12)
,
мм (12)
Расчёт на прочность по напряжениям изгиба
По напряжениям изгиба рассчитывают только зубья колеса, так как витки червяка по форме и материалу значительно прочнее. Точный расчёт по напряжениям изгиба усложняется переменной формой сечения зуба по ширине колеса и тем, что основание зуба расположено не по прямой линии, а по дуге окружности. В приближённых расчётах червячное колесо рассматривают как косозубое. При этом в формулу (4) для косозубой цилиндрической передачи вводят следующие поправки и упрощения.
1. По своей форме зуб червячного колеса прочнее зуба косозубого колеса (примерно на 40%). Это связано с дуговой формой зуба и тем, что во всех сечениях, кроме среднего, зуб червячного колеса нарезан как бы с положительным смещением. Особенности формы зуба учитываются коэффициентом формы зуба YF.
2. Червячная пара сравнительно хорошо прирабатывается, поэтому YY 0,7.
Тогда
формула (4) принимает вид: ,
МПа (13)где: Ft
– удельная расчётная окружная сила;
,
МПа (13)где: Ft
– удельная расчётная окружная сила; ;KF
– коэффициент расчётной нагрузки;mn
– модуль нормальный: mn
= mcos.Коэффициент
формы зуба выбирается по таблицам в
зависимости от эквивалентного числа
зубьев колеса
;KF
– коэффициент расчётной нагрузки;mn
– модуль нормальный: mn
= mcos.Коэффициент
формы зуба выбирается по таблицам в
зависимости от эквивалентного числа
зубьев колеса
 .
.
Расчётная нагрузкаДля червячных передач приближённо принимаютKH = KF = KvK,где: Kv – коэффициент динамической нагрузки;K - коэффициент концентрации нагрузки.
Как отмечено выше, одним из достоинств червячной передачи является плавность работы. Поэтому динамические нагрузки здесь не велики. Хорошая прирабатываемость материалов червячной пары уменьшает неравномерность нагрузки по длине зуба. Всё это позволяет при постоянной нагрузке приниматьKH = KF = 1.
Основные преимущества червячной передачи: возможность получения больших передаточных отношений в одной паре; плавность и бесшумность работы; повышенная кинематическая точность; возможность самоторможения при низком КПД.
Недостатки передачи: сравнительно низкий КПД; повышенный износ и склонность к заеданию; необходимость применения для колёс дорогих антифрикционных материалов (бронза); повышенные требования к точности сборки.
Червячную передачу, показанную на рис. 4, называют глобоидной.
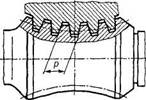
Рис. 4Витки ее червяка расположены на глобоидной (торовой) поверхности. Эта передача появилась сравнительно недавно, имеет повышенную нагрузочную способность (в 1,5—2 раза больше, чем у обычных червячных передач), так как линия контакта в глобоидных передачах располагается благоприятно, что улучшает условия для образования масляных клиньев, и в зацеплении находится большее число зубьев колеса и витков червяка.
Глобоидные передачи требуют повышенной точности изготовления и монтажа, искусственного охлаждения. Эти передачи применяют реже, чем цилиндрические.
