Вопрос 13. Особенности расчета открытых

ПЕРЕДАЧ

Открытые цилиндрические передачи выполняют только прямозубыми и применяют при 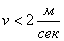 . Степень точности их изготовления по нормам плавности контакта обычно 9-я (по ГОСТ 1643-81),

Основные размеры передач   определяют из расчета на контактную прочность. При расчете принимают допускаемые напряжения 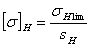  и 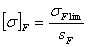 . При любой твердости рабочих поверхностей зубьев открытые передачи считают прирабатывающимися. Учитывая повышенный износ зубьев открытых передач, значение модуля рекомендуется принимать в 1,5. ..2 раза больший, чем для закрытых передач тех же размеров.

Исходные данные для расчета реечных прямозубых передач:

- осевая сила на рейке (окружная сила на шестерне);

- поступательная скорость движения рейки (окружная скорость шестерни);

схема положения шестерни относительно опор.

Предварительное значение делительного диаметра шестерни

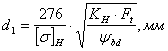
Определяют   (см. разд. 4) и   (см. разд. 6),  . Меньшее значение - при консольном положении шестерни относительно опор.

Модуль передачи:

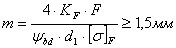
Полученное значение   округляют до ближайшего большего (согласно ГОСТ 9563-60).

Определяют   (см. разд. 4) и   (см. разд. 6).

Число зубьев шестерни

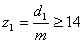
Е сли  , то   надо увеличить до , а    до  . Или принять  , но при этом шестерню необходимо нарезать с положительным смещением инструмента ( ).

Делительный диаметр шестерни:

Частота вращения шестерни: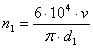

 

Вопрос14. Косозубые цилиндрические передачи. Особые размерные параметры….

1.1 Общие сведения.

Цилиндрические колеса, у которых зубья расположены по винтовым линиям на делительном цилиндре, называют к о с о з у б ы м и (см. рис. 1, б). В отличие от прямозубой в косозубой передаче зубья входят в зацепление не сразу по всей длине, а по­степенно. Увеличивается время контакта одной пары зубьев, в течение которого входят новые пары зубьев, нагрузка передает­ся по большому числу контактных линий, что значительно снижа­ет шум и динамические нагрузки.

Чем больше угол наклона линии зуба β, тем выше плавность зацепления. У пары сопряженных косозубых колес с внешним зацеплением углы β равны, но противоположны по направлению.

Е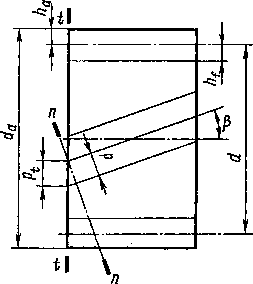 сли к передачам не предъявляют специальных требований, то колеса нарезают правыми, а шестерни — левыми.

У косозубого колеса (рис. 13) расстояние между зубьями можно измерить в торцовом, или окружном (t – t) , и нормальном (п – n) направлениях. В первом случае получим окружной шаг p_t, во втором — нормальный шаг р. Различными в этих направле­ниях будут и модули зацепления:

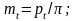
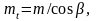
Рис. 13. Геометрические размеры

косозубого колеса

где m_t и m — окружной и нормальный модули зубьев.

Согласно рис. 13

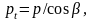
следовательно,

где β - угол наклона зуба на делительном цилиндре.

Нормальный модуль m должен соответствовать стандарту и являться исходной величиной при геометрических расчетах.

Делительный и начальный диаметры

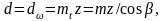
Косозубое колесо нарезают тем же инструментом, что и пря­мозубые. Наклон зуба получают поворотом инструмента на угол β. Профиль косого зуба в нормальном сечении соответствует исходному контуру инструментальной рейки и, следовательно, совпадает с профилем прямого зуба модуля т.

Высоты головки косого зуба h_a и ножки h_f соответственно равны:

Диаметр вершин

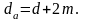
Межосевое расстояние

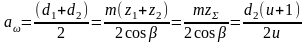
В косозубой передаче, меняя значение угла β, можно незначительно изменить а_w.

Прямозубую передачу можно рассматривать как частный случай косозубой, у которой которой β = 0