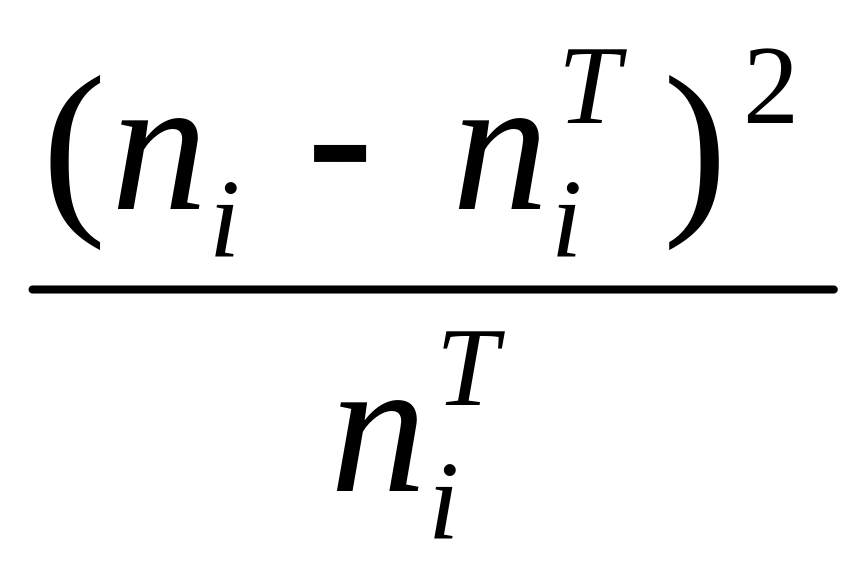1.6. Проверка гипотезы о нормальном распределении случайной величины по критерию Пирсона

Для проверки гипотезы о нормальном распределении случайной величины Х сравнивают между собой экспериментальные и теоретические частоты по критерию Пирсона:

Статистика имеет распределение с V = k – r – 1 степенями свободы, где k – число интервалов эмпирического распределения, r – число параметров теоретического распределения, вычисленных по экспериментальным данным. Для нормального распределения число степеней свободы равно:

V = k – 3

В теории математической статистики доказывается, что проверку гипотезы о модели закона распределения по критерию Пирсона можно делать только в том случае, если выполняются следующие неравенства:

N ≥ 50 ≥ 5 где i = 1,2,3…

Из результатов вычислений, приведенных в таблице 5.1 следует, что необходимое условие для применения критерия согласия Пирсона не выполнены, т.к. в некоторых группах < 5. Поэтому те группы вариационного ряда, для которых необходимое условие не выполняется, объединяют с соседними и, соответственно, уменьшают число групп, при этом частоты объединенных групп суммируются. Так объединяют все группы с частотами < 5 до тех пор, пока для каждой новой группы будет выполняться условие ≥ 5.

При уменьшении числа групп для теоретических частот соответственно уменьшают и число групп для эмпирических частот. После объединения групп в формуле для числа степеней свободы V = k – 3 в качестве k принимают новое число групп, полученное после объединения частот.

Результаты объединения интервалов и теоретических частот для таблицы 7 приведены соответственно в таблице 8.

Результаты вычислений из таблицы 8 можно использовать для проверки гипотезы о нормальном распределении с помощью критерия Пирсона.

Процедура проверки гипотезы о нормальном распределении случайной величины Х выполняется в следующей последовательности:

1. задаются уровнем значимости а = 0,05 или одним из следующих значений: а₁ = 0,01 а₂ = 0,1 а₃ = 0,005

2. вычисляют наблюдаемые значения критерия, используя экспериментальные и теоретические частоты из Таблицы 9.

3. для выборочного уровня значимости а = 0,05 по таблице распределения находят критические значения при числе степеней свободы V = k – 3, где k – число групп эмпирического распределения.

4. сравнивают фактически наблюдаемое с критическим , найденным по таблице, и принимаем решение:

   • если > , то выдвинутая гипотезы о теоретическом законе распределения отвергается при заданном уровне значимости.

   • Если < , то выдвинутая гипотеза о теоретическом законе распределения не противоречит выборке наблюдений при заданном уровне значимости, т.е. нет оснований отвергать гипотезу о нормальном распределении, т.к. эмпирические и теоретические частоты различаются незначительно (случайно).

Таблица 8.

Результаты объединения интервалов и теоретических частот

[4,9; 7,0)	0,13727	8,2362	9	0,5834	0,0708
[7,0; 7,7)	0,237	14,22	14	0,0484	0,0034
[7,7; 8,4)	0,3002	18,012	15	9,0721	0,5037
[8,4; 9,1)	0,21483	12,8898	15	4,453	0,3455
[9,1; 10,5)	0,10801	6,48016	7	0,2702	0,0417
Σ	0,9973	59,8382	60		0,9651

При выбранном уровне значимости а = 0,05 и числе групп k = 5, число степеней свободы V = 2.

По таблице для а = 0,05 и V = 2 находим = 5,99147.

В результате получаем:

Для = 0,9651, которое мы нашли по результатам вычислений, приведенных в Таблице 1.8, имеем:

= 0,9651 < = 5,99147

Следовательно, нет оснований отвергать гипотезу о нормальном распределении случайной величины Х.