1.5. Параметрическая оценка функции плотности распределения
Исходя из гипотезы, что заданная выборка имеет нормальный закон распределения, найдем параметрическую оценку функции плотности, используя формулу для плотности распределения вероятности нормального закона:
Где
и
известны – они вычисляются по выборке.
= 0,9287 = 7,9886
Значения этой функции
вычисляются для середины частичных
интервалов вариационного ряда, т.е. при
х =
.
На практике для упрощения вычислений
функции
,
где i = 1,2,…, k,
пользуются таблицами значений функции
плотности стандартной нормальной
величины.
Для этого вычисляем
значения
для i = 1,2,…, k,
затем по таблице 6 находим значение
.
=
0,0051
=
0,0355
=
0,1415
=
0,3144
=
0,3982
=
0,2850
=
0,1163
=
0,0270
И после вычисляем
функцию:
0,0055
0,4288
0,0382
0,3069
0,1524
0,1252
0,3385
0,0291
Таблица 6
Плотность вероятности
нормального распределения
Функция
,
вычисленная при заданных параметрах
и
в середине частичного интервала,
фактически является теоретической
относительной частотой, отнесенной к
середине частичного интервала.
Поэтому для определения
теоретической частоты
,
распределенной по всей ширине интервала,
эту функцию необходимо умножить на
.
где h = 1,33
где n
= 60
Результаты вычислений вероятностей и соответствующих частот приведены в таблице 7.
Сравнение
экспериментальных и теоретических
частот по критерию Пирсона с целью
проверки гипотезы о нормальном
распределении возможно только в том
случае, если для каждого частичного
интервала выполняется условие
.
Результаты вычислений приведенные в
Таблице 1.7 показывают, что это условие
выполняется не везде. Поэтому те частичные
интервалы, для которых частоты
,
объединяем с соседними. Соответственно
объединяем и экспериментальные частоты
.
Таблица 7
Результаты вычисления экспериментальных и теоретических вероятностей и частот
[xi-1; xi) |
|
|
|
|
|
|
|
|
[4,9; 5,6) |
1 |
5,2468 |
0,0166 |
0,0238 |
-2,95 |
0,0055 |
0,00385 |
0,231 |
[5,6; 6,3) |
0 |
5,9468 |
0 |
0 |
-2,2 |
0,0382 |
0,02674 |
1,6044 |
[6,3; 7,0) |
8 |
6,6468 |
0,1333 |
0,1905 |
-1,44 |
0,1524 |
0,10668 |
6,4008 |
[7,0; 7,7) |
14 |
7,3468 |
0,2333 |
0,3333 |
-0,69 |
0,3385 |
0,23695 |
14,217 |
[7,7; 8,4) |
15 |
8,0468 |
0,25 |
0,3571 |
0,06 |
0,4288 |
0,30016 |
18,0096 |
[8,4; 9,1) |
15 |
8,7468 |
0,25 |
0,3571 |
0,82 |
0,3069 |
0,21483 |
12,8898 |
[9,1; 9,8) |
4 |
9,4468 |
0,0666 |
0,0952 |
1,57 |
0,1252 |
0,08764 |
5,2584 |
[9,8; 10,5) |
3 |
10,1468 |
0,05 |
0,0714 |
2,32 |
0.0291 |
0,02037 |
1,2222 |
Σ |
60 |
|
0,9998 |
|
|
|
0,9972 |
59,8332 |
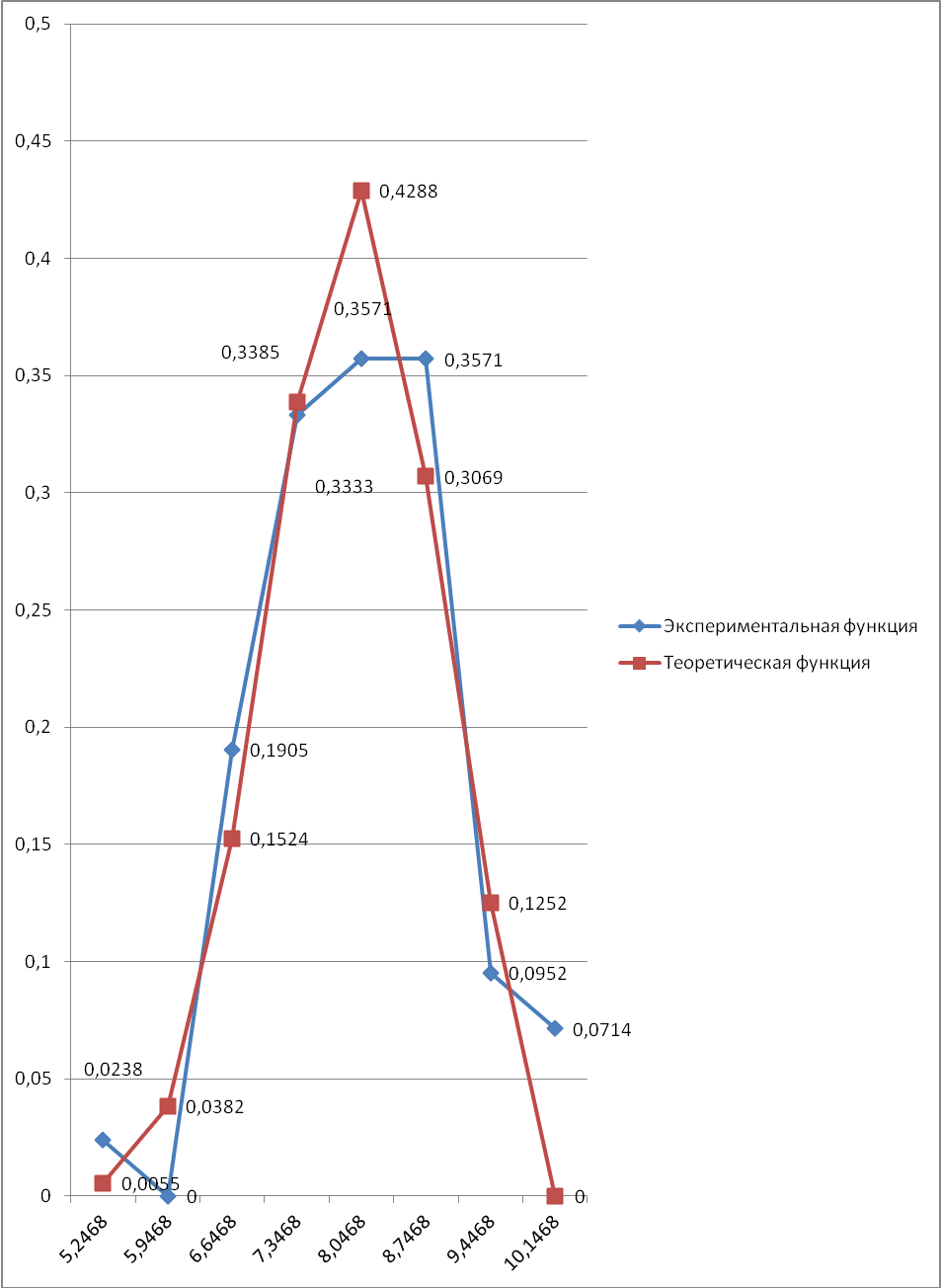
Построим графики экспериментальной и теоретической плотности нормального распределения:
Рис. 1 Теоретическая и экспериментальная функции плотности распределения
