28. Композиційно-номінативні модальні логіки (кнмл). Транзиційні, темпоральні кнмл.

Під композиційно-номінативною модальною системою в загальному випадку розуміємо об'єкт вигляду _= (Cms, Ds, Dns). Тут Cms, Ds та Dns означають наступне.

1) Cms=(D, R, Pr, C) – композиційна модальна система, яка задає семантичні аспекти світу. Її компоненти D, R, Pr, C визначаються таким чином.

Множину D трактуємо як множину станів світу.Множина R – це множина відношень на станах світу вигляду RDDⁿ.

Множина Pr – це множина предикатів вигляду D{T, F}. Множина C – це множина композицій на Pr .

2) Ds – дескриптивна система КНМС; вона визначає множину стандартних дескрипцій – формул мови модальної логіки.

3) Dns – денотаційна система КНМС; вона визначає значення кожної стандартної дескрипції.

Композиційно-номінативні модальні логіки кванторного та реномінаційного рівня

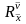Алфавіт мови КНМЛ реномінаційного рівня складається з множини V предметних імен, множини Ps предикатних символiв, символів базових композицій , , та множини Мs символів базових модальних композицій.

Множина Fт формул такої мови визначається індуктивно:

1) Кожний PPs є формулою. Такi формули назвемо атомарними.

2) Нехай  та  – формули. Тодi  та  – формули.

3) Нехай  – формулa. Тодi ()– формула.

4) Нехай  – формулa. Тодi x – формула.

5) Нехай  – формула, – символ базової модальної композиції. Тодi  – формула.

Транзиційні композиційно номінативні модальні логіки

Для ТМС множина R відношень на станах світу складається з відношень вигляду RDD, які природно назвати відношеннями переходу. Якщо R складається з єдиного бінарного відношення, яке позначатимемо , то таку ТMС назвемо стандартною (СТMС).

Відношення  базоване, якщо воно визначене на множині базових даних А та продовжене на множину ^VA наступним чином:

1) d h  im(d)im(h);

2) для всіх vim(d) якщо vad і vbh, то a b.

Для випадку базованого відношення  стандартні ТМС назвемо базованими.

СТМС із базовими модальними композиціями  і  називають загальними ТМС.

Для загальних ТMС відображення інтерпретації Jт стосовно формул вигляду  та  уточнимо наступним чином.

Для кожних dD визначимо:

Jт()(d) =

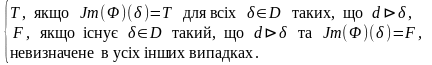
Jт()(d) =

Розглянемо тепер окремий дуже важливий випадок транзиційних модальних логік – темпоральні, або часові модальні логіки.

СТMС із базовими модальними композиціями _ (завжди буде), _ (завжди було), _ (колись буде) та _ (колись було), назвемо темпоральними КНМС (ТмКНMС). Композиції _, _, _, _ назвемо базовими часовими композиціями.

Jт(_)(d)

Як і для випадку загальних ТМС, залежно від властивостей відношення  отримуємо відповідні темпоральні КНМС.