Результаты вычисления интервальных оценок для математического ожидания и дисперсии.
Для вычисления интервальной оценки математического ожидания воспользуемся формулой:
Где а = М[X] – математическое ожидание
n – 1 = V = 59 – число степеней свободы
tv;p
– величина, численно равная половине
интервала, в который может попасть
случайная величина
,
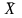имеющая определенный закон распределения
при заданной доверительной вероятности
Р и заданном числе степеней свободы V.
Подставляем
в формулу вычисленные ранее значения
,
и n.
Задаемся доверительной вероятностью:
Р1 = 0,95 Р2 = 0,99
Для каждого значения Рi (i=1,2) находим по таблице значения t59;p и вычисляем два варианта интервальных оценок для математического ожидания.
При Р1 = 0,95 t59;0,95 = 2
При Р2 = 0,99 t59;0,99 = 2,66
Для интервальной оценки дисперсии существуют следующие неравенства:
Поставляем
в неравенство известные значения
и n,
получим неравенство, в котором неизвестны
и
.
Задаваясь
доверительной вероятностью Рi
(или
уровнем значимости а)
вычисляем значения
и
.
Используем эти два значения и степень
свободы V
= n
– 1 = 59, по таблице находим
и
.
=
=
=
=
и
- это границы интервала, в который
попадает случайная величина Х, имеющая
распределение вероятности Рi
и заданной степени свободы V
(V=59).
Д
ля
Р1
= 0,95
и
находим
по таблице:
=
= 40,4817
=
= 83,2976
Поставляя в неравенства и и, вычисляя, получим интервальную оценку.
П
ри
Р2
= 0,99
и
находим
по таблице:
=
= 35,5346
=
= 91,9517
Поставляя в неравенства и и, вычисляя, получим интервальную оценку.
Для интервальной оценки среднеквадратического отклонения имеем:
При Р1 = 0,95 получаем доверительный интервал:
= 0,9803
При Р2 = 0,99 получаем доверительный интервал:
1.4. Результаты ранжирования выборочных данных и вычисление моды и медианы
Используя исходные данные, запишем все заданные значения выборки
в виде неубывающей последовательности значений случайной величины X,
представленные в таблице 1.1.
Таблица 1.1
Ранжированный ряд
-1,52 |
0,0229 |
0,2949 |
0,7639 |
1,0203 |
1,2573 |
1,9443 |
-1,3792 |
0,036 |
0,3386 |
0,7914 |
1,0327 |
1,3757 |
2,2538 |
-1,3056 |
0,0405 |
0,4715 |
0,8162 |
1,0554 |
1,3908 |
2,3198 |
-1,0776 |
0,0906 |
0,4988 |
0,8324 |
1,1391 |
1,5082 |
2,3808 |
-0,5349 |
0,1095 |
0,5791 |
0,854 |
1,1685 |
1,5849 |
2,3933 |
-0,3745 |
0,1607 |
0,594 |
0,8565 |
1,2214 |
1,6518 |
2,4819 |
-0,3454 |
0,1618 |
0,6165 |
0,883 |
1,2291 |
1,7445 |
2,7887 |
-0,209 |
0,2174 |
0,6229 |
0,8928 |
1,249 |
1,7559 |
2,8705 |
-0,0081 |
0,2327 |
0,6414 |
0,9245 |
|
|
|
Интервал [1,52;2,8705], содержащий все элементы выборки, разобьём на частичные интервалы, используя при этом формулу Стерджеса для определения оптимальной длины и границ этих частичных интервалов.
По формуле Стерджеса длина частичного интервала равна:
Для удобства и простоты расчётов округлим величину h. В нашем случае выбираем h =0,6 и вычисляем границы интервалов.
За начало первого интервала принимаем значение:
Далее вычисляем границы интервалов.
= -1,82 +
0,6 = -1,22
= -1,22 +
0,6 = -0,62
= -0,62 +
0,6 = -0,02
= -0,02 +
0,6 = 0,58
= 0,58 +
0,6 = 1,18
= 1,18 +
0,6 = 1,78
= 1,78 +
0,6 = 2,38
= 2,38 +
0,6 = 2,98
Вычисление границ заканчивается, как только выполняется неравенство Xn > Xmax, то есть X8 = 2,98 > Xmax = 2,8705.
По результатам вычислений составляем таблицу. В первой строке таблицы помещаем частичные интервалы, на второй строке – середины интервалов, в третьей строке записано количество элементов выборки, попавших в каждый интервал – частоты, в четвертой строке записаны относительные частоты и в пятой строке записаны значения плотности относительных частот или значения выборочной, экспериментальной функции плотности. Значения выборочной функции плотности представлены в таблице 1.2
Таблица 1.2
Значение выборочной функции и плотности
[xi-1; xi) |
|
ni |
|
|
[-1,82; -1,22) |
-1,52 |
3 |
0,05 |
0,083 |
[-1,22; -0,62) |
-0,92 |
1 |
0,016 |
0,027 |
[-0,62; -0,02) |
-0,32 |
5 |
0,083 |
0,138 |
[-0,02: 0,58) |
0,28 |
14 |
0,23 |
0,38 |
[0,58; 1,18) |
0,88 |
18 |
0,3 |
0,5 |
[1,18; 1,78) |
1,48 |
11 |
0,183 |
0,305 |
[1,78; 2,38) |
2,08 |
3 |
0,05 |
0,083 |
[2,38; 2,98) |
2,68 |
5 |
0,083 |
0,138 |
По результатам вычислений функции плотности, представленной в Таблице, можно сделать вывод, что мода имеет 1 локальный максимум в окрестности точки х = 0,88 и с частотой по n = 18.
Оценку медианы находим, используя вариационный ряд, для которого:
n = 2k; k = n / 2 = 60 / 2 = 30
Сравнение
оценок медианы
и оценки математического ожидания
