§ 5. Коэффициент полезного действия трансформатора

■ Под коэффициентом полезного действия трансформа­тора (к. п. д.) понимают отношение отдаваемой трансфор­матором активной мощности Р₂ к подведенной активной мощности Р₁ , т. е.

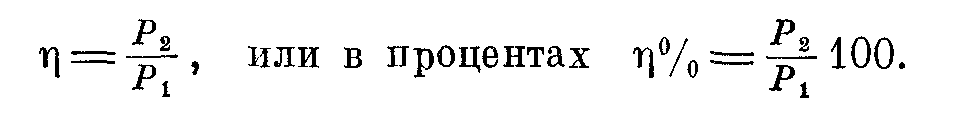
К. п. д. можно определить, измерив отдаваемую и под­водимую мощности при полной нагрузке трансформатора и взяв отношение этих мощностей. Такой метод опреде­ления к. п. д. называют прямым. Прямой метод опреде­ления к. п. д. применения не нашел, так как он неэко­номичен вследствие того, что трансформатор нужно на­гружать на полную мощность, что вызывает большой расход электроэнергии при испытании большого коли­чества трансформаторов. Этот метод также неточен, так как при измерении больших мощностей неизбежны зна­чительные погрешности.

В практике к. п. д. определяют косвенным путем.

Известно, что с достаточной точностью потери в стали трансформатора можно определить из опыта холостого хода Р_cт ≈ Р₀, а потери в меди из опыта короткого замы­кания Р_м ≈ Р_к при номинальной нагрузке трансформа­тора. Тогда подведенная к трансформатору мощность P₁ = Р₂ + P_ст + Р_м. а к. п. д. определится из отношения

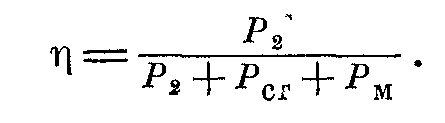Мощность Р₂, отдаваемую трансформатором при любой нагрузке, можно определить по формуле

где k_нг — коэффициент нагрузки трансформатора.

Так как Р_к выражает потери в меди только при номи­нальной нагрузке трансформатора, то потери в меди трансформатора при любой его нагрузке можно опреде­лить по формуле

k_нг берется в квадрате потому, что при постоянном напряжении ток изменяется пропорционально нагрузке, а потери в меди пропорциональны квадрату тока нагрузки. Тогда формула для определения к. п. д. трансформатора при любой его нагрузке будет иметь следующий вид:

В этой формуле S_н подставляют в ква, а Р₀ и Р_к в квт.

Определим, при каком значении коэффициента на­грузки к. п. д. будет максимальным, т. е. найдем опти­мальный коэффициент нагрузки.

Для этого нужно взять первую производную и приравнять ее нулю.

Исследование данной функции на максимум дает следующий результат:

значит к. п. д. трансформатора будет максимальным при такой нагрузке, когда потерив стали равны потерям в меди, т. е. постоянные потери равны переменным.

К постоянным потерям относят потери в стали, так как они от нагрузки не зависят, а к переменным — потери в меди обмоток, так как они зависят от нагрузки.

Из уравнения Р₀ = k²_нгР_к находим:

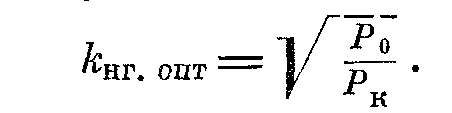
В современных трансформаторах отношение

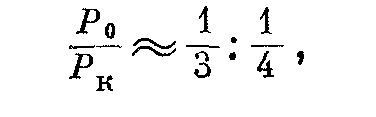
а значение оптимального коэффициента нагрузки:

В современных трансформаторах к. п. д. очень высок и достигает 98—99%. Примерная кривая к. п. д. транс­форматора и кривая изменения потерь в стали и меди от коэффициента нагрузки приведены на рисунке 102.

Пример 3. Найти к. п. д. трансформатора и наивыгод­нейший коэффициент нагрузки, если S_н = 240 ква; Р₀ = = 1400 вт; Р_к = 4900 вт; cos φ₂ = 0,8; k_нг = 1

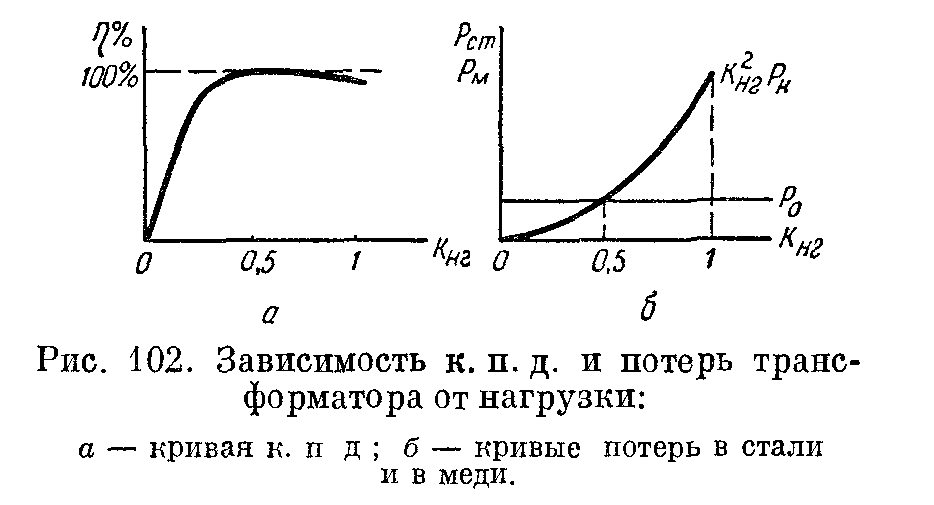
Решение. Находим к. п. д. трансформатора по формуле

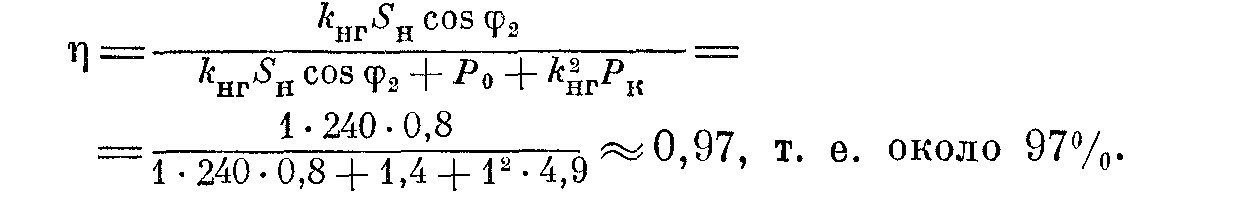
Находим наивыгоднейший коэффициент нагрузки, при котором к. п. д. трансформатора будет максимальным:

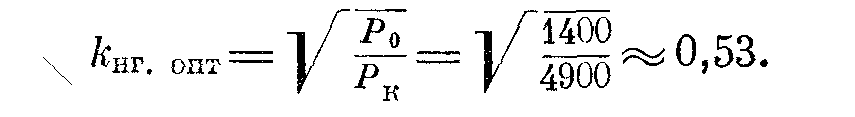
Вопросы для самопроверки

1. Расскажите, как и для чего проводят опыт холостого хода трансформатора?

2. Расскажите, как и для чего проводят опыт короткого замы­кания трансформатора?

3. Для чего делают приведение вторичных величин к первичной обмотке?

4. Нарисуйте и объясните схему замещения трансформатора.

5 Нарисуйте и объясните полную векторную диаграмму трансформатора при индуктивной нагрузке.

6. Нарисуйте и объясните упрощенную векторную диаграмму трансформатора при индуктивной нагрузке и соответствующую ей схему замещения.

7 Как определить параметры короткого замыкания транс­форматора?

8. Выведите формулу для определения ΔU трансформатора аналитическим методом

9 Объясните формулу для определения кпд трансформа­тора

10 Как определить наивыгоднейший коэффициент нагрузки трансформатора, при котором кпд трансформатора будет наи­большим?

11 Объясните уравнение равновесия э д с в трансформаторе.

12 Объясните уравнение м д с трансформатора