Канонические уравнение прямой. Прямая с угловым коэффициентом. (21)

Любой ненулевой вектор, параллельный данной прямой, будем называть направляющим вектором этой прямой.

Рассмотрим следующую задачу: найти уравнение прямой, проходящей через данную точку М1(х1, у1) и имеющей заданный направляющий вектор q={l, m}. Очевидно, точка М(х, у) лежит на указанной прямой тогда и только тогда, когда вектора М1М = { x- x1, y – y1} и q = {l , m} коллинеарны, то есть тогда и только тогда, когда координаты этих векторов пропорциональны (x-x1)/l = (y – y1)/m. Это уравнние называется каноническим уравнением прямой.

Уравнение у = кх + б называется уравнением прямой с угловым коэффициентом. В этом уравнение К обозначает угловой коэффициент данной прямой, а Б представляет собой велечину отрезка, отсекаемого данной прямой на оси Оу, начиная от начала координат.

Угол между двумя прямыми, условие параллельности и перпендикулярности двух прямых. (22)

1) Пусть 2 прямые Л1 и Л2 заданы общими уравнениями (Л1 = А1х + В1у + С1 = 0; А2х + В2у + С2=0). Так как нормальны векторм Л1 являет вектор n1 = {A1, B1}, а нормальным вектором Л2 n2 = {A2, B2}, то .

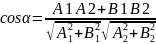Условие пераллельности прямых Л1 и Л2, эквивалентное условие коллинеарности векторов н1 и н2, заключается в пропрорциональности координат этих векторов, т.е. имеет вид А1/А2 = В1/В2.

Условие перпендикулярности прямых Л1 и Л2 возможно пи cos α = 0 и имеет вид А1А2+В1В2=0.

2) Теперь две прямые Л1 и Л2 заданы каноническими уравнениями (Л1 = х-х1/л1 = у-у1/м1; Л2 = х-х2/л2 = у-у2/м2). Так как направляющими векторами прямых Л1 и Л2 служат вектор q1 = {l1, m1} и q2 = {l2, m2}, то угол между прямыми определяется формулой .

Условием параллельности прямых Л1 и Л2, эквивалентное условию колинеарности q1 и q2, заключается в пропорциональности координат этих векторов, т.е. имеет вид л1/л2 = м1/м2.

Условие перпендикулярности прямых Л1 и Л2 может быть при cos α = 0 и имеет вид л1л2 + м1м2=0.

3) Прямые Л1 и Л2 заданы уравнениями с угловым коэффициентом (Л1 = у =к1х + б1; Л2 = у = к2х + б2). Если α1 и α2 – углы наклона прямых Л1 и Л2 к оси Ох, а α один из углов между эими прямыми, то α = α2 – α1 и tg α = tg (α2 – α1) = (tg α2 - tg α1)/(1 + tg α1tg α2) = (k2-k1)/(1+k1k2).

Усливия параллельности прямых Л1 и Л2 имеет вид к1 = к2.

Условие перпендикулярности прямых Л1 и Л2 может быть получено при условии, что тангенс угла α не существует, то есть обращается в нуль знаменатль, 1+к1к2=0

Нормированное уравнение прямой, отклонение точки от прямой. (23)

Уравнение x cosθ + y sinθ – p = 0 называется нормированным уравнение прямой. Р – длина отрезка. Θ – угол между вектором n и осью Ох.

Отклонением δ точки М от прямой L называется число +д в случает, когда точка М и начало координат О лежат по разные стороны от прямой Л, и число –д в случае, когда М и О лежат по одну сторону от Л. Если начало координат О лежит на прямой Л, отклонение равно +д в случае, когда М лежит по ту сторону от Л, куда направлен вектор n, и равным –д в противном случае.

Левая часть нормированного уравнения прямой равно отклонению точки М с координатами x, y от прямой Л, определяемой этим уравнением.

Для нахождения отклонения δ точки М(х0, у0) от прямой Л следует в левую часть нормированного уравнения прямой Л подставить на место х и у координаты х0 и у0 точки Л.

Для приведения общего уравнения прямой Ах + Ву + С = 0 к нормированному виду x cosθ + y sinθ – p = 0 следует умножить его на нормирующий пножитель 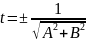, знак которого противоположен знаку С.