Свойства определителей 2 порядка: решение систем уравнений второго порядка. (1)

Определителем второго порядка, соответствующим матрице, называется число, равно а₁₁а₂₂ – а₁₂а₂₁. Элементы, составляющие матрица данного определителя, называются элементами этого определителя.

Свойства:

1. Величина определителя не изменится, если строки и столбцы этого определителя поменять местами.

2. Перестановка двух строк (столбцов) определителя равносильна умножению его на число (-1).

3. Если определитель имеет две одинаковые строки (столбцы), от он равен нулю.

4. Умножение всех элементов некоторой строки (столбца) определителя на число λ равносильно умножению определителя на это число λ.

5. Если все элементы некоторой строки (некоторого столбца) определителя равно нуль, то и определитель равен нулю.

6. Если элемент двух строк (столбцов) определителя пропорциональны, то определитель равен нулю.

7. Если каждый элемент н-й строки (столбца) определителя представляет собой сумму 2 слагаемых, то определитель может быть представлен в виде суммы 2 определителей, первый из которых имеет в н-й строке (столбца) первых из упомянутых слагаемых и те же элементы, что и исходный определитель, в остальных строках (столбцах), а второй определитель имеет в н-й строке (столбце) второй из упомянутых слагаемых и те же элементы, что и исходный определитель, в остальных строках (столбцах)

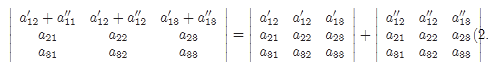
8. Если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель λ, то величина определителя не изменится.

Определители 3 порядка и их свойства. (2)

Определителем 3 порядка, соответствующим матрице, называется число равно 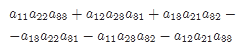. Элементы, составляющие матрица данного определителя, называются элементами этого определителя. Диагональ, образованная элементами а₁₁, а₂₂, а₃₃ является главной диагональю, а элементами а₁₃, а₂₂, а₃₁ – побочной.

Алгебраические дополнения и миноры. (3)

Алгебраическим дополнение элемента а_i,j матрица А называется число А_i,j=(-1)^i+j * на минор_i,j.

Минором данного элемента определителя н-го порядка называется определитель (н-1)-го порядка, получаемый из данного определителя путем вычеркивания той строки и того столбца, на пересечении которых стоит данный элемент.

Алгебраических дополнения и миноры связаны между собой по следующему правилу: алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со знаком плюс, если сумма номеров строки и столбца, на пересечении которых стоит данный элемент, если число четное, и со знаком минус – в противном случает.

Сумма произведений элементов какого-либо столбца определителя на соответствующие алгебраические дополнения элементов этого (другого) столбца равно величине этого определителя (равно нулю).

Обратная матрица. (4)

Квадратная матрица называется вырожденной (или особенной), если ее определитель равен нулю, и невырожденной (неособенной), если ее определитель не равен нулю.

Матрица Б называется обратной матрицей для матрицы А, если произведение А*Б=Б*А=Е. Так как произведение матриц не перестановочно (А*Б != Б*А), то вводят понятие правой и левой обратных матрица А*Б (Б – правая обратная) Б*А (Б – правая обратная).

Всякая невырожденная матрица А имеет единственную обратную матрицу (левая и правая матрицы совпадают). Для неквадратных матрица и вырожденных матриц обратных матриц не существует.

Свойства:

Ранг матрицы. (5)

Наибольшим из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Ранг обозначается как r, r(A) или rang A.

Минор, порядок которого определяет ранг матрицы, называется базисным минором. У матрицы может быть несколько базисных миноров.

Для вычисления матрицы используются элементарные преобразования матрицы: перестановка местами 2 параллельных рядом матрицы, умножение всех элементов ряда матрицы на число, отличное от нуля, прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Свойства ранга матрицы: При транспонировании матрицы ее ранг не меняется; если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится; ранг матрицы не изменяется при элементарных преобразованиях матрицы.

Ранг канонической матрицы равен числу единиц на главной диагонали.

Решение систем уравнений 3 порядка. Правило Крамера. (6)

Правило Крамера x_j = 1/∆ * ∆_j . Формула означает, что если матрица квадратной системы не вырождена, то система имеет единственное решение, система будет определена (теорема Крамера).

Теорема Крамера. (7)

Если основная матрица квадратной системы линейных уравнений невырожденная, то такая система имеет единственное решение.

Если определитель основной матрицы квадратной системы линейных уравнений равен нулю, то теорему Крамера для нахождения решений системы применить нельзя.

Неоднородная система трех линейных уравнений с тремя неизвестными с определителем, равным нулю. (8)

Решений нет.

Однородная система трех линейных уравнений с тремя неизвестными. (9)

Если определеитель равен 0, то бесчисленное множество решений. Если определитель не равен нулю, то только тривиальные решения.

Метод последовательного исключения неизвестных. (10)

Самый распространенный метод решения любых систем линейных уравнений – это метод последовательного исключения неизвестных из системы и называется он методом Гаусса.

Преобразуя системы в процессе ее решения, мы должны быть уверены, то каждое преобразование не искажает множества решений исходной системы, то есть система, полученная после применения очередного преобразования, имеет те и только те решения, которые имеет исходная система.

Две системы линейных уравнений с одним и тем же числом неизвестных называются эквивалентными, или равносильными, если они несовместны либо обладают одними и теми же решения, то есть всякое решение одной системы является решением другой и наоборот.

Следующие преобразования системы линейных уравнений называются элементарными: перемена местами (транспозиция) любых двух уравнений системы; умножение обеих частей любого уравнения системы на число, отличное от нуля; прибавление к любому уравнению системы любого уравнения этой системы, умноженного на число; удаление из системы уравнений, у которых все коэффициенты и свободный член равны нулю.

Применение любого элементарного преобразования к системе линейных уравнений приводит к эквивалентной системе.