6. Відтворення динамічної зміни значень параметрів моделі з перебігом часу.

Нехай потрібно промоделювати дифузійне зменшення концентрації речовини в приземному шарі (до 1 м) у кожній точці простору протягом 200 сек. Початкові концентрації у кожній точці простору представлені значеннями матриці Concentration. Додаткові умови – 1) повітря спокійне (тобто відсутня турбулентна дифузія;) 2) шар приземний – до 1 м (вважатимемо, що в цьому шарі концентрація не змінюється на різній висоті).

Приклад ідеалізації: відсутність горизонтальної дифузії Зробимо одне важливе припущення, яке ідеалізує дану модель з тієї точки зору, що горизонтальна дифузія на даний момент не відбувається, тобто речовина не потрапляє з однієї точки простору в іншу в горизонтальному напрямку через те, що швидко піднімається в верхній шар за межі 1 м. (наприклад – газоповітряна суміш тепла, або речовина легша за повітря). Якщо таке припущення не зробити в даному випадку, то довелося б враховувати баланс мас цієї речовини для кожної комірки, інтенсивність надходження речовини до кожної комірки й вибування з неї. Для прикладу скористаємось випадком вертикальної дифузії.

Визначаємо хід часу

Time:=0 .. 200

Нехай відомий закон зміни концентрації протягом часу, який описується формулою

,

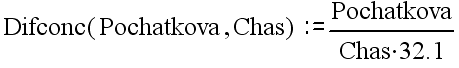Де Difconc – назва функції (від «дифузійне зменшення концентрації»)

Pochatkova – значення початкової концентрації в конкретній точці

Chas - проміжок часу, який минув з моменту викиду речовини у початковій концентрації.

Pochatkova/(Chas*32.1) - операція, що потрібна для розрахунку концентрації в момент часу Chas

Ця функція обраховує точкові значення, які задаються єдиним значенням концентрації (у одній точці), але на протязі певного часу. Результатом її застосування до точки з концентрацією 10 протягом часу Time:=0 ..100 є масив значень: концентрація в першу, другу, третю … (і т.д.) … двохсоту секунди (див. ілюстрацію нижче):

Для одного елементу це відображене на графіку:

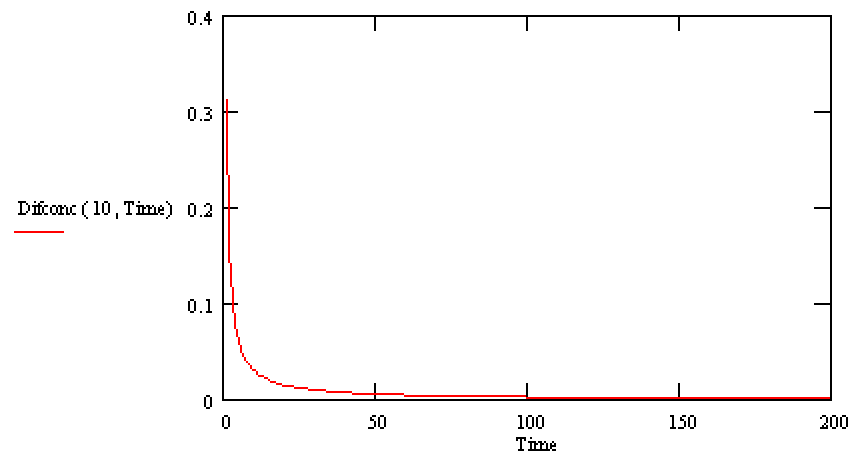
Рис. 4. Графік зміни концентрації речовини у точці з початковою концентрацією 10 протягом 200 сек.

Завдання. Запишіть на аркуші Mathcad попередній приклад та відобразіть результат на графіку.

7. Відтворення просторової динаміки значень параметрів моделі з перебігом часу

Якщо обійти матрицю концентрацій (25 елементів) у циклі і застосувати до неї функцію Difconc, то буде отримано 25 х 200 значень (на кожну точку простору – по 200 значень концентрації, які зменшуються протягом 200 сек.). Це має бути матриця з 25 елементами (5 х 5) кожен з яких є вектором з 200 елементами. При іншому порядку обходу це має бути матриця з 200 елементами, кожен з яких є матрицею з 25 елементами (5 х 5). Отримання такої матриці безпосередньо не має сенсу через великий об’єм пам’яті, який вона займала. В кожен момент часу програма робочого аркушу може звернутись до конструкції типу:

,

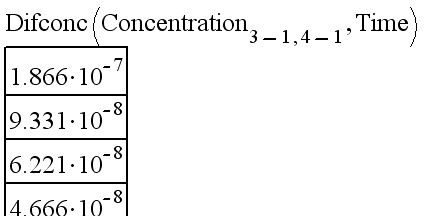
де розраховується динаміка концентрацій для комірки з координатами (3,4)

Завдання. Запишіть на аркуші Mathcad попередні приклади