Лабораторна робота № 2. Особливості використання Mathcad для побудови імітаційних моделей – (4 год.)
Зміст роботи.
Частина 1.
Визначення простору у одно- і двовимірних комірних імітаційних моделях. Визначення перебігу часу у імітаційних моделях. Зв’язування значень параметрів просторово розподілених об’єктів і процесів із координатами в межах моделі.
Частина 2.
Циклічні операції в Mathcad. Відтворення динамічної зміни значень параметрів моделі з перебігом часу. Відтворення просторової динаміки значень параметрів моделі з перебігом часу.
Хід роботи
Повторюйте всі описані дії та виконуйте завдання самостійно там де це вказано.
Частина 1 (2 год.)
1. Визначення простору у одновимірних імітаційних моделях.
Для того щоб визначити одномірний простір необхідно визначити інтервальну змінну, значення якої будуть відповідати відстані від початку координат у обраних одиницях вимірювання. Різниця значень двох сусідніх значень буде задавати розмір комірки моделі.
Визначимо відстань (наприклад вздовж русла річки) у 100 метрів з кроком 1 метр.
Послідовність натискання клавіш така (все вводиться без пробілів):
Пишемо «Ruslo» (це - ім’я інтервальної змінної)
Натискаемо «=», з’являється символ :=
Вводимо «0» (перший елемент)
Натискаємо клавішу «:» (в англійській розкладці, клавіша з крилічною літерую «ж»)
Вводимо «100» (останній елемент)
Вводимо «*»
Вводимо «m» (це - одиниця вимірювання)
Перевіримо що знаходиться у змінній:
Пишемо «Ruslo»
Натискаемо «=»
Вивід має виглядати як висока таблиця із значеннями:
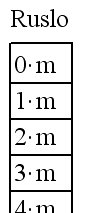
Якщо одиниці вимірювання постійні, то можна обходитись і без них
Змінимо крок моделі, збільшивши його до 10 м.
Змінимо крок моделі, зменшивши його до 0,2 м.
Завдання. Визначить відстань у 1500 м з кроком 50 м
2. Визначення простору у двовимірних імітаційних моделях.
У двовимірних моделях ми маємо справу з двома осями, орієнтованими перпендикулярно одна до іншої, наприклад – вісь абсцис і ординат, або вісь абсцис і аплікат.
Для цього використовуємо двовимірний масив – прямокутну матрицю.
Визначимо ділянку ґрунту 100*100 метрів з кроком 25 м квадратною матрицею.
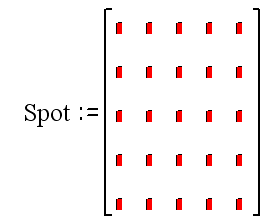
Сперш визначаємо кількість комірок моделі 1+(100/25)=5
Визначаємо матричну змінну, вводимо її ім’я, наприклад, «Spot».
Натискаємо «=»
Натискаємо сполучення клавіш Ctrl+M
У віконці “Insert Matrix” вказуємо кількість рядків і стовпчиків матриці
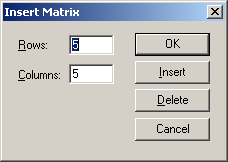
У віконці “Insert Matrix” натискаємо кнопку «ОК»
В цій моделі ділянки початок відліку знаходиться у комірці з значенням «0». Значення відстаней на самих осях легко заповнити вручну.
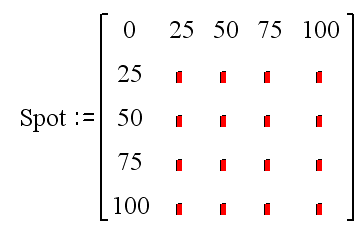
Значення ж відстані у проміжних комірках необхідно обраховувати за теоремою Піфагора.
Так у квадраті
0 – 25
| |
25 - ?
відсутнє значення розраховується як
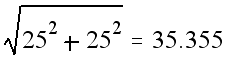
Пізніше ми навчимось робити це автоматично для всієї матриці, а зараз просто заповнимо її значеннями.
Здійснення доступу до значення певної комірки (елементу матриці)
Яка відстань від початку координат до початку границі комірки з координатами (x=3, y=4)
Відлік нумерації елементів матриці в Маткаді ведеться від 0 (тобто по горизонталі маємо елементи з номерами 0, 1, 2, 3, 4), тому треба використати координати (2, 3). Здійснюємо доступ.
Послідовно вводимо: «Spot[2,3=» і получаємо значення
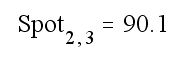
Завдання. Отримайте значення елементу матриці Spot з координатами (4,5)
Для того, щоб здійснювати доступ до елементів одномірних масивів, їх також треба визначати як матриці.