Задача 1. Решить задачу выпуклого программирования.

Составим функцию Лагранжа:

Теперь запишем условия равенства нулю частных производных функции, условие дополняющей нежёсткости и, т.к. ищется минимум функции, условие неотрицательности всех .

1. Рассмотрим случай :

→

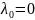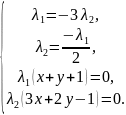
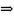Получаем нулевые решение отсутствует (Лагранжиан не может быть равен 0)

2. Рассмотрим случай :

2.1) Пусть :

→ →

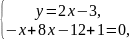→ не является точкой минимума , т. к. не выполняются начальные условия

2.2) Пусть

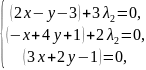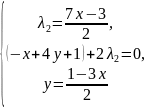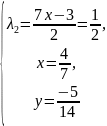→ → → → не является точкой минимума , т. к. не выполняются начальные условия

2.3) Пусть :

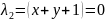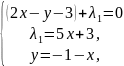→ → → точка минимума выполняются начальные условия.

2.4) Пусть :

→ →

→

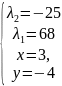
- не может быть точкой минимума.

_{ЗАДАЧА 2. Решить задачу линейного программирования графическим методом}. Во всех вариантах

Будем использовать в качестве базисных переменных x₃, x₄, x₅ и выделять именно их, решая систему методом Гаусса. Запишем систему в матричном виде и решим:

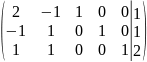
(1-2x+y≥0 , 1+x-y≥0 ,2-x-y≥0 , x≥0 , y≥0)

Построим график системы:

Для получения координат точки минимума исследуемой функции проводим линию уровня нашей целевой функции. Линию уровня для получения минимального значения нужно передвигать влево (т.к. функция прямо пропорциональна x₁) и вверх (т.к. функция обратно пропорциональна x₂) от градиента до крайней точки многоугольника.

Точка минимума находится на пересечении двух прямых, задаваемых уравнениями:

Таким образом, точка M(1/2, 3/2) является точкой минимума данной функции.

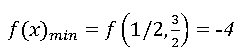
Задача 3. Решить задачу № 2 симплекс-методом, используя в качестве первоначальной крайней точки.

_{- крайняя точка.}

– наша функция.

Т.к. мы будем искать минимум функции, применим симплекс метод применяется для поиска минимума функции..

αij	x1	x2	βi
x3	2	-1	1
x4	-1	1	1
x5	1	1	2
f(x)	4	-8	-6	pj

_{Ищем среди коэффициентов pi (коэффициентов целевой функции) pi<0, берем соответствующий этому элементу столбец (кроме столбца свободных членов). Для выбора опорного элемента необходимо найти, какой из них удовлетворит условию минимума отношения свободного члена к данному элементу:} , причем

После выбора опорного элемента совершаем пересчет таблицы:

- опорный элемент заменяем на единицу, деленную на опорный элемент;

- опорную строку делим на опорный элемент;

- опорный столбец делим на опорный элемент и умножаем на минус единицу;

- остальные элементы считаем по «правилу определителя» и делим на опорный элемент

- совершаем эти итерации до тех пор, пока в нижней строке все элементы (кроме свободного члена) не станут положительными.

αij x1 x2 βi x3 2 -1 1 x4 -1 1 1 x5 1 1 2 f(x) 4 -8 -6 αij	x1	x4	βi
x3	1	1	2
x2	-1	1	1
x5	2	-1	1
f(x)	-4	8	2

αij	x5	x4	βi
x3	-1/2	3/2	3/2
x2	1/2	1/2	3/2
x1	1/2	-1/2	1/2
f(x)	2	6	4

Таким образом мы нашли минимум, ответ сошелся с предыдущей задачей.

x_min=(1/2 , 3/2 , 3/2 , 0 , 0)