
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:Mat.Modelirovani1e.docx
X
- •Основные понятия и определения
- •Введение. Определение математической модели
- •Структура мм
- •Пример составления математической модели
- •Три пути проведения научных исследований.
- •Свойства математической модели.
- •Дуальная классификация математической модели.
- •1 3 2 Нестационарные стационарные
- •Физическое моделирование и теория подобия
- •Моделирование и подобие.
- •Размерные и безразмерные величины.
- •Примеры применения.
- •2.4.1 Установившееся течение несжимаемой жидкости в трубе. Гидродинамика.
- •2.4.2. Теплообмен при течении в горизонтальной трубе.
- •Построение математической модели на основе законов сохранения
- •3.1 Общая форма законов сохранения.
- •Примеры применения.
- •3.2.1 Уравнение баланса тепла в стержне
- •3.2.2 Уравнение неразрывности для одномерного течения в трубе.
- •3.2.3 Уравнение динамики кс.
3.2.2 Уравнение неразрывности для одномерного течения в трубе.
Рассмотрим движение в трубе. (l >> d)
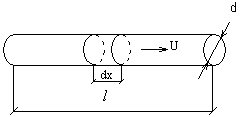
Полагаем, параметры потока неизменимы по поперечному сечению.
Рассмотрим элемент dV.
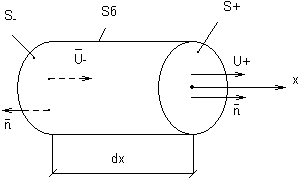
Запишем
уравнение (3.2) для нашей задачи:
 ,
,



Рассмотрим:

Рассмотрим левую часть:

Собираем соотношение:

Поскольку
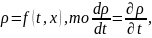 делим наше уравнение на dx
и переходим к пределу:
делим наше уравнение на dx
и переходим к пределу:
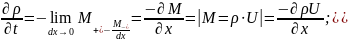
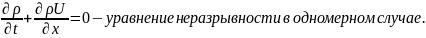
3.2.3 Уравнение динамики кс.
С точки зрения математического моделирования, в данном случае будем строить нуль мерную модель.

Запишем
соотношение (3.2) для данной задачи (для
КС), при этом:
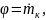

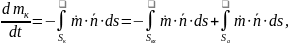
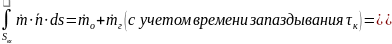

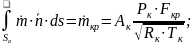
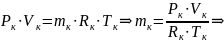
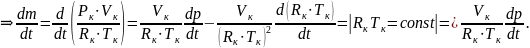
Собираем:
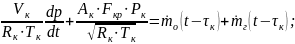

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
