Основные понятия и определения

1. Введение. Определение математической модели

Математическая модель (ММ) – соотношения между переменными и параметрами, и переменных описываемых моделируемый объект (МО) записанный языком математики.

Переменные задачи – переменные, которые изменяются внутри одного МО.

Параметры задачи – переменные, которые меняются от объема к объему.

Моделируемый объект

Физическая модель

Математическая модель

Анализ ММ

Алгоритм решения

Программное обеспечение

Схема 1. Этапы математического моделирования

Физическая модель – устная или схематическая, схематическое описание МО.

ММ, ФМ – записанные на языке математики.

На схеме приведено полный цикл создания ММ, в реальности часть пунктов могут быть исполнены.

При создании ММ МО всегда первичен (правдоподобность результат получения при физическом и математическом моделировании должна соотносится с реальным МО).

2. Структура мм

x—

g

y

MO

x = x_i i=1.N - вектор входных параметров;

y = y_i i=1.M - вектор выходных параметров;

g = g_i i=1.K - вектор внутренних параметров системы или МО.

(Для проектанта РН при МО-РД входные параметры – компоненты топлива, внутренние параметры – геометрические параметры РД, выходной параметр – тяга).

(1.1)

В общем случае :

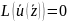(1.2)

Где

1. – частный случай (1.2).

3. Пример составления математической модели

(Движение материальной точки в поле силы тяжести, в атмосфере).

1. Моделируемый объект – материальная точка, движущаяся в атмосфере Земли.

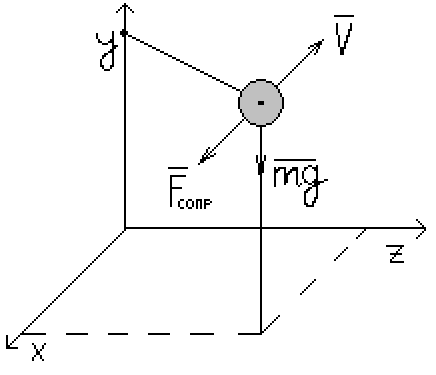
2. Физическая модель.

Материальная точка движется под действием двух сил, силы тяжести и силы лобового сопротивления F_сопр.

Вектор F_сопр, как вектор любой силы трения, противоположен направлению скорости V.

3. Составление математической модели.

Запишем второй закон Ньютона – основное уравнение нашей модели, из которого будем получать:

,

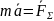Получим выражение для действующих сил:

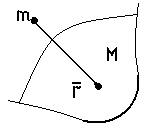
, где

r² – расстояние между материальной точкой и центром Земли.

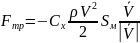, где

C_x – коэффициент лобового сопротивления.

S_м – площадь материальной точки.

В данной задачи на материальную точку действуют две силы, с чего следует, что траектория будет лежать в одной плоскости образованной пересечением двух направлений (силы тяжести, силы сопротивления). Следовательно, задача из трёхмерной становится двухмерной.

В паре ММ + моделируемый объект, всегда первичен (он всегда один, а ММ можно составить бесконечное множество).

Введение системы координат – одна из главных составляющих математического моделирования, их тоже может быть бесконечное множество. Вводить её нужно таким образом, чтобы максимально упростить математическую модель. Перерисуем мат. модель.

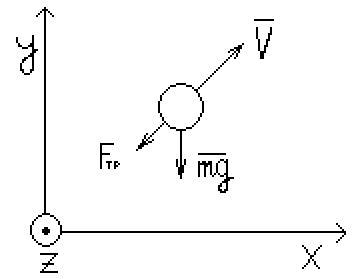
Z – материальная точка.

Поскольку предполагается рассматривать движение в атмосфере, то сравнение толщины атмосферы порядка 100 км и радиус Земли 6400 км, даёт предположение пренебречь и изменением от высоты полёта:

.

В плоскости движения можно использовать декартовую систему координат. В таком случае уравнение движения имеет вид:

(1.3)

Спроецируем уравнение движения на систему координат:

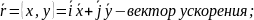
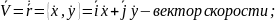
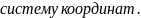
Поскольку при сделанных допущениях вектор силы тяжести это постоянная величина, то одну из осей системы координат выбрать ему колинеарно.

Спроецируем (1.3) на ось:

Решение уравнений третьего уровня (1.4) – тривиально.

.

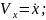
4. Анализ математической модели.

Упрощение модели (отбросить несущественные слагаемые). Обычно это делается приведением модели к безразмерной форме, при этом для каждого слагаемого появляется дополнительный коэффициент.

Интуитивно, в получении модели можно пренебречь учётом лобового сопротивления.

Н.У:

5. Алгоритм решения уравнения модели.

Для упрощённой модели, это уравнение выполнено аналитически (см. выше).

Для инженеров пункт 1.5 и 1.6, для инженерных расчётов –решены, реализованы, для инженеров нужно только выбрать реализацию (MathCad, Mathlab, Математика).