27. Метод нормальных координат

С калярное произвед. 2-х векторов опред.:

Вектор X пускай обозначает действие постоянной силы, а вектор Y – перемещение точки приложения этой силы. Тогда их произведение будет выражать работу силы Х на пути У.

Вектора называются ортогональ-ными, если их скалярное произведение = 0.

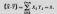
Т.е. суммарная работа сил Xi равна нулю на перемещениях Yi.

Д ля системы с n степенями свободы k-ый прогиб во времени изменяется по закону:

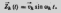
Вектор сил инерции:

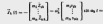
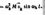
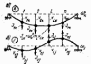
При sin(w_kt)=1, вектор внешних сил: и соответствующие прогибы Vk(рис.). В этом состоя-нии система находится в равно-весии.Для аналогичного состояния системы j-ой формы:

и прогиб Vj.

Составим условие взаимности работ для этих двух состояний: или

Скалярные произведения векторов одинаковы,поэтому переносим все в левую часть и выносим

В общем случае ω k≠ωj, поэтому

- равенство выражает условия взаимной ортогональности любых двух форм собственных колебаний из спектра этой системы. Собственные колебания совер-шаются так, что возможная работа сил инерции (внешних сил) одной формы на перемещениях другой формы равна нулю.

28. Динамический метод определения устойчивости

Расчет заключается в исследовании сооружений при кинематических воздействиях на фундамент.

У прощенная задача сводится к расчету защемленной стойки, несущую несколько масс, на заданное смещение.

Каноническое уравнение:

Иногда применяют другую форму, считая, что перемещение масс склады-вается из перемещений от смещений фундамента Δ и перемещений вследствие из-гиба стойки:

Инерционная сила, приложен-ная в i-ой массе:

Не знаю как но приходим к этому уравнению:

Оно позволяет перейти от заданных перемещений к заданным силам, так как инерционная сила нам известна.

29. Уравнения движения при сейсмическом воздействии. Акселерограммы.

Сейсмическими воздействиями называются такие, которые возникают при колебаниях земной коры и передаются через фундамент на конструкцию, при этом конструкция испытывает дополнительные инерционные нагрузки.

Здание рассматриваем как защимленный стержень с расположенными на нем точечными массами. Каждой массе заданы перемещения, а основанию передано ускорение:

Судя по всему, перемещения приложенные к конструкции записываем в виде:

Необходимо учесть и действие y(t):

Суммируем потому как смещение массы происходит не только под действием x, но и y.

Получаем:

По 2-му з-ну Ньютона, сила равна массе на ускорение в квадрате(P(t)=m*(Y с двумя точ-ками), подставляем в уравнение с раскрытыми скобками получаем:

- это и есть i-ое уравнение движения.

Акселерограмма–график зависи-мости от времени абсолютного ускорения данной точки поверхности земли (или места крепления изделия), возникающего в результате землетрясения.

По ним производятся расчеты сооружений на прочность.

30. Продольно-поперечный изгиб балок

Продольно-поперечным изгибом называется сочетание поперечного изгиба со сжатием или растяжением бруса.

В практике инженерных расчетов под продольно-поперечным изгибом подразумевают обычно случай действия сжимающей силы и поперечной нагрузки.

Рассмотрим методику такого расчета на примере балки, шарнирно опертой по концам, нагруженной поперечными силами, направленными в одну сторону, и сжимающей силой S (рис. 7.6).

.

Здесь

.

Следовательно,

    (7.5)

В целях упрощения решения предположим, что дополнительный прогиб   изменяется по длине балки по синусоиде, т. е. что  . Данное уравнение для шарнирно опёртой по концам балки соответствует форме потери устойчивости.

Заменим в формуле (7.5) прогиб   выражением  :

,

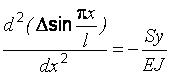или

,

или

,

откуда

.

Выражение   совпадает с формулой Эйлера для критической силы сжатого стержня с шарнирно закрепленными концами. Поэтому ее обозначают Р_Э  и называют эйлеровой силой.

Следовательно,

(7.6)

Область применения формулы (7.6) лежит в интервале 0 ≤ S ≤ 0,8 Р_Э.

И з формулы (7.6) следует, что соотношение между полными прогибами балки y и прогибами  , вызванными действием только поперечной нагрузки, зависит от отношения S/P_Э (величины сжимающей силы S к величине P_Э эйлеровой силы). Таким образом, отношение S/P_Э  является критерием жесткости балки при продольно-поперечном изгибе; если это отношение близко к нулю, то жесткость балки велика, а если оно близко к единице, то жесткость балки мала, т. е. балка является гибкой.

В случае, когда S = 0, прогиб  , т. е. при отсутствии силы S, прогибы вызываются только действием поперечной нагрузки.

Когда величина сжимающей силы S приближается к значению эйлеровой силы P_Э, полные прогибы балки резко возрастают и могут во много раз превышать прогибы  , вызванные действием только поперечной нагрузки. В предельном случае, при S = P_Э, прогибы y, подсчитанные по формуле (7.6) становятся равными бесконечности.