3 Методика и алгоритм решения задачи в условиях неопределенности

Решение принимается в условиях неопределенности, ког­да невозможно оценить вероятность потенциальных результатов.

В неопределенной операции могут быть известны множество состояний обстановки и эффективность систем для каждой из них, но нет данных, с какой вероятностью может появиться то или иное состояние. Единого критерия оценки эффективности для неопределенных ситуаций не существует. Наиболее часто в неопределенных ситуациях используются критерии:

– среднего выигрыша;

– Лапласа;

– осторожного наблюдателя (Вальда);

– максимакса;

– пессимизма-оптимизма (Гурвица);

– минимального риска (Сэвиджа).

Критерий «Лапласа»: Данный критерий предполагает задание вероятностей состояния обстановки . Эффективность системы оценивается как среднее ожидаемое значение (МОЖ) оценок эффективности по всем состояниям обстановки

оптимальной системе будет соответствовать эффективность

У точняющая модель для оценки по критерию Лапласа представлена на рисунке 2.

Рисунок 2 – Уточняющая модель для оценки по критерию Лапласа

4 Тестирование разработанного программного средства

Для проверки правильности оценки необходимо сверить результат, выдаваемый программой, с результатом аналитического расчета.

Выбор в программе задачи №3 на Рисунке 3.

Рисунок 3 – Выбор задачи №2

4.1 Тестирование оценки системы в условиях определенности

Исходя из условия, что все полученные критерии равнозначны, можем применить формулу для расчета оценки эффективности.

Таблица 2 – Исходная таблица данных

	0,5	0,1	0,3	0,25
	0,2	0,4	0,5	0,5
	0,1	0,2	0,1	0,4

Производим оценку важности критериев (1-4 чем ниже тем значимее критерий):

К₁=1 К₂=2 К₃=3 К₄=4

Определяем размер уступка:

α =0,1

Находим максимуму k_j:

max(k₁)=0,5 max(k₂)=0,4 max(k₃)=0,5 max(k₄)=0,5

Ищем разницу между 1 и 2 по важности критерия и сравниваем с уступкам

/max(k₁)- max(k₂)/<= α /0,5-0,4/<=0,1

Оптимальная альтернатива а₂=0,5 (по первой важности критерия k₁)

Результат работы программы для данного метода представлен на Рисунке 4.

Рисунок 4 – Результат работы программы для лексикографической оптимизации.

Из полученных результатов можно сделать вывод, что алгоритм в программе реализован верно.

4.2 Тестирование оценки системы в условиях неопределенности

Исходные данные представлены в Таблице 1. Рассчитаем эффективность систем по критерию Среднего выигрыша, используя формулу:

Находим среднее ожидаемое значение по столбцам:

К₁ = (0,5 + 0,2 + 0,1)/3= 0,27;

К₂ = (0,1 + 0,4 + 0,2)/3 = 0,23;

К₃ = (0,3 + 0,5 + 0,1)/3 = 0,3;

К₄ = (0,25+ 0,8+ 0,4)/3 = 0,48;

Ищем максимум среди средних значений:

К(опт)=К₄=0,48

Следовательно, оптимальным критерием будет К(опт)= К₄.

Результат работы программы для данного метода представлен на Рисунке 5.

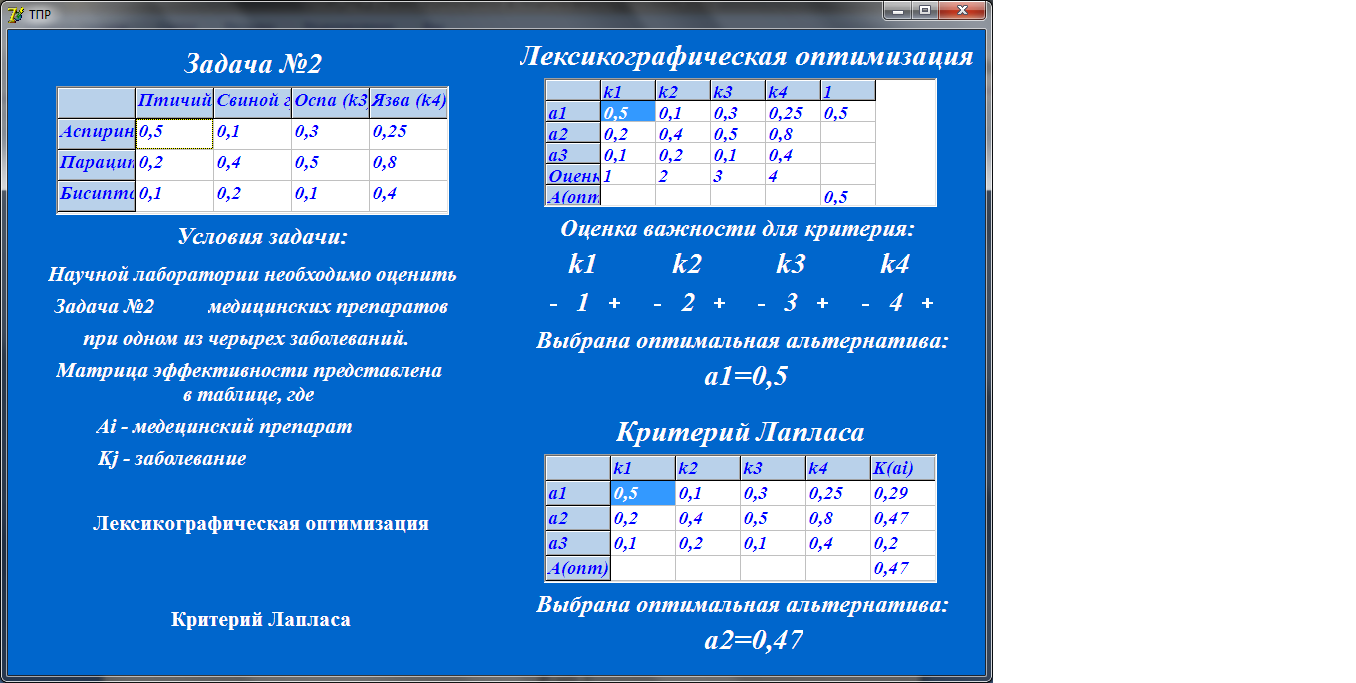
Рисунок 5 – Результат работы программы для критерия Лапласа

Следовательно, результаты расчёта совпали, можно сделать вывод, что алгоритм реализован верно.