Питання для самоконтролю

1. дати означення комплексного числа

2. сформулювати означення уявної одиниці.

3. як знайти степінь уявної одиниці?

4. які комплексні числа називають рівними, спряженими?

5. за якими правилами виконують дії над комплексними числами?

6. запишить загальний вигляд комплексного числа у тригонометричній формі.

7. запишить загальний вигляд комплексного числа у показниковії формі.

Змінні величини і функції

Нехай X і Y – деякі числові множини, нехай x X, y Y.

Якщо кожному значенню змінної х поставлено у відповідність одне значення змінної y, то кажуть що визначена функціональна залежність y від x по закону y = f (x).

При цьому х називається залежною змінною.

Множина Х – область визначення (існування) функції, множина Y – область значень (зміни) функції.

Сукупність точок координатної площини xoy, які задовольняють рівнянню

y = f (x) називається графіком цієї функції.

Вправи

В задачах 1 – 3 побудувати по точках на відрізку графіки вказаних функцій.

1. 1) y = 2x; 2) y = 2x + 2; 3) y = 2x – 2 .

2. 1) y = x ; 2) y = x + 1; 3) y = x - 1.

3. 1) y = ; 2) y = + 1; 3) y = - 1.

В одній і тій же системі координат побудуйте графіки функцій.

4. 1) y = cos x 2) y = 2 cos x 3) y = -cos

5. 1) y = log x 2) y = log (x - 2) 3)y = - log (x - 2)+2

6. 1) y = 2) y = 3) y = - 1

7. 1) y = sin x 2) y = - 3) y = - + 2

Знайдіть значення функції

8. в точках - ; - ; 0; .

В задачах 9– 11 знайдіть області визначення функцій.

9. 1) y = 2) y = 3) y =

10. 1) y = 2) y =

11. 1) y = - 2) y =

Побудуйте графіки функцій.

1) y = 2) y =

12. Вказати, які з даних функцій парні і які непарні:

1). f (x) = 2).

3). F(x) = 4).

13. Знайдіть область визначення тригонометричних функцій:

1.) y = 2.) y =

14. Знайдіть область значень тригонометричних функцій:

1. y = 2 2. y = 2 + 3cos5x

15. Доведіть, що функція f (x)=tg періодична і знайдіть її найменший додатній період.

Границі послідовності та функції. Нескінченно малі та нескінченно великі

1. Число а називається границею послідовності (границею змінної ), якщо для всякого знайдеться залежне від число таке, що для всіх натуральних . Інтервал - називається околом числа а. Отже, означає, що для всього знайдеться таке число , що для всіх числа будуть знаходиться в - околі числа а.

2. Границя функції. Нехай функція f (x) визначена в деякому - околі точки a, за виключенням можливо самої точки a. Кажуть, що число b границя функції f (x) при при , або ), якщо для любого >0 існує залежне від число таке, що при .

Якщо і при цьому х < 0, то пишуть , якщо і при цьому x > a, то пишуть .

- границі зліва функції f (x) в точці а.

- границі справа функції f (x) в точці а.

3. Нескінченно малі

Якщо , тобто якщо при , то - називається нескінченно малою при .

4. Нескінченно великі.

Якщо для будь-якого нескінченно великого числа N існує таке , що при виконується нерівність , то функція називається нескінченно великою при

Вправи

1. Покладаючи n = 0;1;2;3…, записати послідовність значень змінних:

1. 2. 3.

2. Починаючи з якого n модуль кожної із змінних стане і буде залишатися менше 0,001; менше даного додатного ?

3. Записати послідовність значень змінної . Починаючи з якого n модуль різниці x – 1 стане і буде залишатися менше 0,01; менше даного додатного ?

4. Довести, що . Для даного числа >0 знайти найбільше число таке, що для будь –якого x на - околі числа 3 значення функції y = 2x – 1 опиниться в - околі числа 5. Показати графічно

5. Довести, що . Із якого найбільшого - околу числа -1 треба взяти значення х , щоб значення функції y = 3 – 2x - x відрізнялося від її границі менше ніж на = 0,0001?

6. Довести, що . Пояснити таблицями значень x і при x = 1;10;100;1000;…

7. Довести, що .При яких x значення функції буде відрізнятися від своєї границі менше ніж на 0,001?

8. Довести, що . При яких значеннях x x значення функції буде відрізнятися від своєї границі менше ніж на 0,01?

9. Напишіть послідовність:

10. 1) 2) 3)

11. 4) 5) 6)

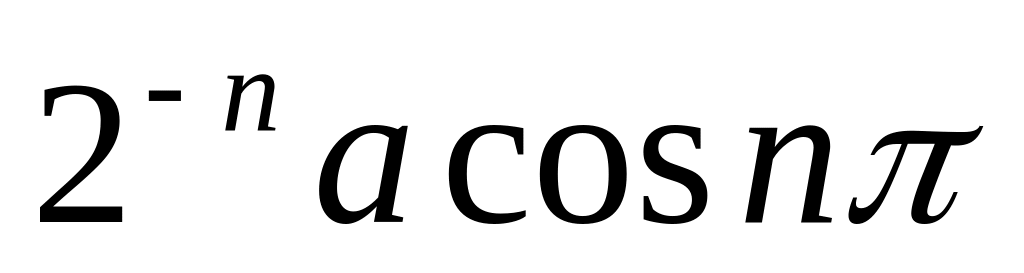
12. Чи існує в кожному прикладі та чому вона дорівнює ?

13. Довести, що вказуючи, що різниця є величина нескінченно мала при x нескінченно великому. Пояснити таблицями, покладаючи x = 1;10;100;1000… .

Властивості границь.

Розкриття невизначеностей виду і

1. Границя постійної дорівнює самій постійній.

якщо lim u і lim існують

4. , якщо lim u і lim ≠ 0.

Вправи

Знайти границі:

1. 1). 2)

2. 1) (пояснити таблицю) 3.

4. 5.

6. 7.

8. 9.

10. 11.

12. 13.

14 1) 2) 3)

15. 16.

17. 1) 2)

18. 19 . 20. 21. 22. 23. 24. 25. 26. 27. 28. 29.