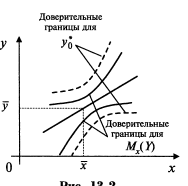
7.Доверительные интервалы регрессионных оценок. Доверительные интервалы коэффициентов линейной регрессии. Доверительный интервал предсказанной величины по уравнению линейной регрессии.

Параметры: N –num. of data; Xmin; Xmax; X_ev=sum(x_i)/N – оценка мат. ожидания; S² – выборочная дисперсия (оценка дисперсии) S² =sum(x_i-x_ev)²/(N-1); S=sqrt(S²)

Интервальной оценко парметра С называется числовой интревал котоорый с заданной вероятностью р накрывает неизвестное значение параметра С. Такой интервал называется доверительным, а вероятность – доверительной вероятность. Предельная ошибка выборки – наибольшее отклонение оценки от оцениваемого параметра.

Регрессия7Y=ax+b линейная регрессия. Рассчитываем коэф. X0 – х. Подставляем в уравнение Y=ax0+b. Для указания точности, нужны доверительные интервалы – средне квадратичное отклонения на коэффециент delta=s*phi (в общем виде). S^2= S^2e + S^2y+ S^2x

S=aqrt(S^2).

Для линейной парной регрессии. Значимость оценивается по критерию Фишера, по дисперсии. Высчитывем коэффициент A*=rxy*Sy/Sx. Проверка значимости , с константами стьюденат (распределение Стьюдента)

A=a*+-delpa a*

Steps:

1Выбор вида зависимости (линейная, логарифмическая и тд.), из здравого смысла, на глаз

2Расчет коэф. Зависимости. Для зависимости y=ax+b: по Методу Наименьших Квадратов

Требование чтобы сумма :sum(y^-_i - y_i)^2 или

s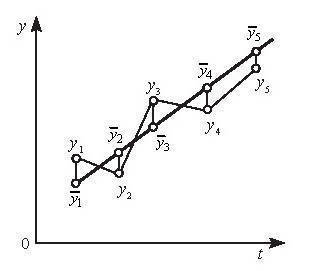 um(ax_i+b – y_i)^2. Минимумы достигаются когда частные производные равны нулю. Из решения системы получается:

а=ryx*Sy/Sx

b=y_ev-a*x_ev

3 Оценка значимости и адекватности выбранной модели

Считается , где

SS – квадратичная изменчивость (регрессионная и ошибки) S²_r=SSr/(k-1) and S²_e=SSe/N-k, где k – число компонентов в анализе, N – общее кол-во данных. Сравниваем по Фишеру.

то регрессия значима.

Доверительный интревал 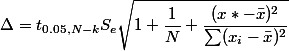; y=y*+Δ

8.Закон распределения случайных ошибок Гаусса. Мера точности.

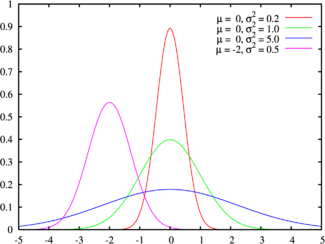Мера точности -  характеристика рассеяния значений случайной величины. h связана с квадратичным отклонением σ формулой

        

         Этот способ измерения рассеяния объясняется тем, что в случае нормального распределения плотность вероятности случайной величины с М. т. h и математическим ожиданием а записывается формулой

         , V=s/X_{среднее}

9.Корреляционный анализ и его применение для решения геологических задач. Корреляция в закрытой числовой сис­теме. Корреляция в замкнутой системе отражает только свойства системы. Так часто для замкнутой системы равно -1. Она называется ложная корреляция.

Корреляционная зависимость между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой. Нахождение линейной зависимости. Zxy=Zyx=sum(xi-xev)(y-yev)/(σ xσy*(N-1)), σ – стандартные отклонения. (или функция коррел(…;…)). Критерий значимости: 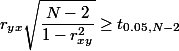, если больше значит значима.

10.Корреляция между порядковыми величинами. Ранговый коэффициент корреляции Спирмена. Коэффициент ранговой корреляции Кендалла.

Ранговая корреляция. Коэффициент ранговой корреляции Спирмена rs имеет несложный порядок расчета, поэтому в естественных науках ему отдается предпочтение. Ранжирование производится по описанному принципу. В случае наличия двух или более одинаковых значений берут среднее арифметическое из двух соседних рангов, которые они должны занять, и каждому значению приписывается полученное среднее арифметическое(например, если в выборке есть два значения, равные181,2, их они должны поделить между собой14 и15 ранги, то каждому из них пишется ранг(14+15)/2=14,5). Подобная операция делается и при большем количестве

равных значений.

Коэфициент Спирмена где R – ранги. Для повторяющиеся рангов , mi объем группы с повторяющимися рангами, Кенделл это дополнения с Ti (учет повторений рангов)

11.Коэффициент частной корреляции и оценка его значи­мости. Rxy,z=(rxy-rxz*ryz)/((1-rxz^2)*(1-ryz)^2)

12.Критерий Пирсона, его использование при решении гео­логических задач.

Критерий согласия Пирсона или Х².Проверка гипотезы о том что случайная величина Х подчиняется некоторому определенному закону распределения. Распределение Х² дает возможность оценить степень согласования теоритического и статистического распределений. , кол-во данных.