1. Абсолютные и относительные ошибки. Методы оценива­ния абсолютных случайных ошибок.

Абс. Ошибка - величина расхождения между величиной параметра, определенного на основе выборочного статистического наблюдения и его действительной величиной.

Отн. Ошибка - отношение абсолютной ошибки к действительной величине параметра.

Абс. Ошибку принимается максимальное отклонение от истинного значения или среднего

Отн. Ошибка – отношение Абс. К истинному или среднему значению.

Свойства случайных ошибок :

1. Чем меньше по абсолютной величине случайная ошибка, тем она чаще встречается при измерениях.

2. Одинаковые по абсолютной величине случайные ошибки одинаково часто встречаются при измерениях.

3. При данных условиях измерений величина случайной погрешности по абсолютной величине не превосходит некоторого предела. Под данными условиями подразумевается один и тот же прибор, один и тот же наблюдатель, одни и те же параметры внешней среды. Такие измерения называют равноточными.

4. Среднее арифметическое из случайных ошибок стремиться к нулю при неограниченном возрастании числа измерений.

Оценка абсолютной ошибки:

Для равноточных результатов измерений мерой точности является средняя квадратическая ошибка m, определяемая по формуле Гаусса:

.

Средняя квадратическая ошибка обладает устойчивостью при небольшом числе измерений.

Абсолютно -

2. Анализ последовательностей данных. Временные ряды. Автокорреляционная функция.

ВРЕМЕННОЙ РЯД (или ряд динамики, или динамический ряд) [time series] — ряд последовательных значений, характеризующих изменение показателя во времени (или другой растущей координаты).

Функцию можно представить в виде x=f(t) + e ( тренд + случайная состовляющая).

Тренд— основная тенденция изменения временного ряда. Тренды могут быть описаны различными уравнениями — линейными, логарифмическими, степенными и т. д.

Проверка гипотезы о наличии в последовательности данных линейного тренда ( критерий Аббе) ЗАДАЧА 4.4

- xi – итый элемент, x с черточкой среднее, N – кол-во элементов

Автокорреляционная функция - это характеристика сигнала, которая помогает находить повторяющиеся участки сигнала или определять несущую частоту сигнала, скрытую из-за наложений шума и колебаний на других частотах. Автокорреляционная функция часто используется в обработке сигналов и анализе временных рядов.

3.Вероятность попадания нормально распределенной слу­чайной величины в заданный интервал значений.

Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.

Нормальное распределение, (гауссовым распределением), — распределение вероятностей, которое задается функцией плотности вероятности:

где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.

Функция распределения: случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х. F(x)=P(X<x). Т.е. геометрически это вероятность того, что случайная точка Х попадет левее заданной точки х.

Плотность вероятности: fi(x) непрерывной (только) случайной величины Х, есть производная её функции распределения

Вероятность попадания случайной величины на отрезок [x, x+dx]:

, переходя к приделу dx-0 получаем производную

Вероятность попадания непрерывной случ. Величины в интервал [a,b] равна определенному интегралу от её плотности вероятности в пределах от a till b: , последний переход по формуле Ньютона-Лейбница.

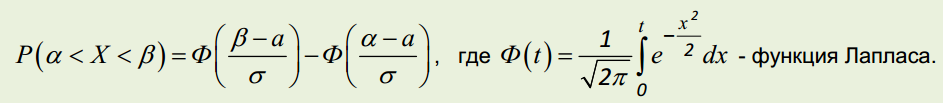
а – мат. Ожидание, сигма – ср. квадратичное отклонение (корень из дисперсии ). Вид функ. Плотн:

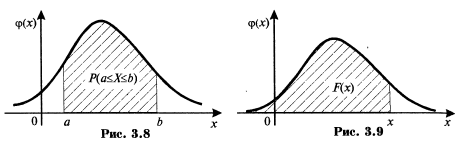, геометрическая интерпретация.