21 Складання абераційних рівнянь для системи із тонких компонентів Составление аберрационных уравнений

В левой части аберрационных уравнений представляют соответствующую сумму Зейделя в форме адаптированной под систему тонких компонентов. Здесь используются параметры Р, С, W, π, Ф.На этом этапе компоненты подлежащие синтезу рассматриваются как тонкие.

Правая часть уравнения содержит нужное значение соответствующей суммы Зейделя. Если левая часть уравнения отображает суммы всей системы, то тогда в правой части обычно записывается 0 или некое значение суммы достижение которого позволяет компенсировать эту же аберрацию высшего порядка, при наличии достоверных сведений о ней.

Часто встречается ситуация, когда система содержит унифицированные компоненты и компоненты конструктивные параметры которых до аберрационного расчета известны: например окуляр и оборачивающая система. В этих случаях в левой части уравнения записывается значение суммы Зейделя, которые соответствуют реальным аберрациям известной части системы и знак при которой(суммы) позволяет аберрациями синтезируемой части компенсировать аберрации известной части системы .

Составление левой части аберрационного уравнения.

Исходными данными для составления левой части являются результаты габаритного и энергетических расчетов из которых становится известными оптические силы всех компонентов расстояние между ними, положение и диаметры зрачков, полевой диафрагмы.

Первым этапом является: расчет хода первого и второго вспомогательных нулевых лучей.

Телескопическую систему разбивают на две части: часть до передней фокальной плоскости окуляра и после.

1-й ВНЛ на входе в первую часть системы должен иметь такие h₁ и α­₁ при которых α­ на выходе первой части системы будет иметь значение 1 соответствующее нормировке 1-го ВНЛ.

В связи с этим нужно определить фокусное расстояние первой части системы и принять h₁ равное этому фокусному расстоянию.

Второй ВНЛ проходит через центр входного зрачка под углом 1.

Второй этап:

Составление суммы Зейделя в левой части.

Сферическая аберрация

i – номер компонента части синтезируемой системы, m – количество компонентов.

h_i – высоты первого ВНЛ, P_i – аберрационный параметр Р, i-го компонента, значение которого не известно и которое должно быть найдено.

Кома ;

H_i – высоты второго ВНЛ на i-м компоненте, I – инвариант Лангранжа-Гельмгольца, W_i – параметр полевых аберраций

Астигматизм

;

Ф_i – оптическая сила i-го компонента (не в диоптриях)

Кривизна поля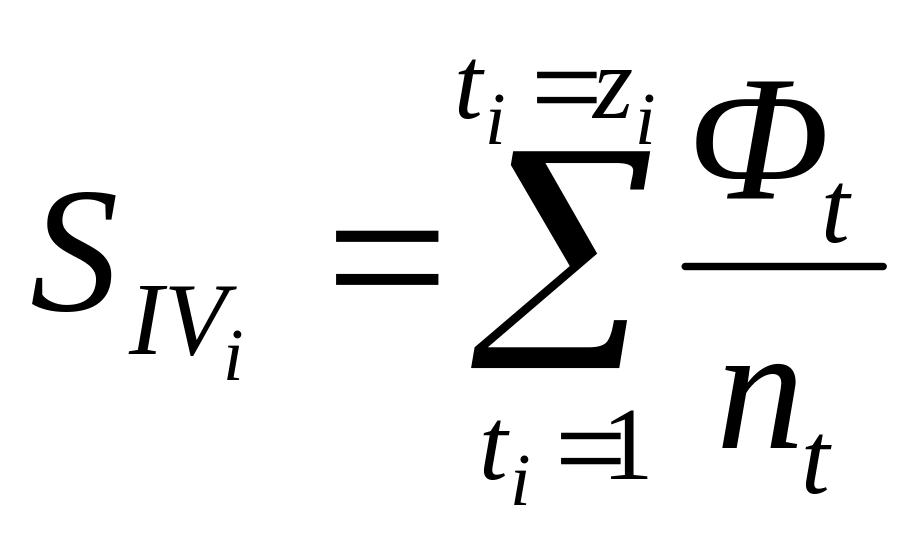

t_i – номер линзы в i-м компоненте, z_i – количество линз в i-м компоненте, Ф_t – оптическая сила линзы с номером t в i-м компоненте, n_t – показатель преломления по основной длине волны материала линзы под номером t.

– нормированная опт сила линзы с номером t . Тогда

,

Если для всех компонентов число одинаковое, то тогда:

Дисторсия ;

Хроматические аберрации.

Хроматические суммы отображающие хроматические аберрации позволяют составить уравнение для хроматических аберраций. Так как эти аберрации имеют иную природу. Как хроматические в них участвует коэффициент хроматизма С_i, который не входит в выражение монохроматических аберраций, поэтому уравнения хроматических составляются и решаются отдельно.

Хроматизм положения

, – хроматизм компонента.

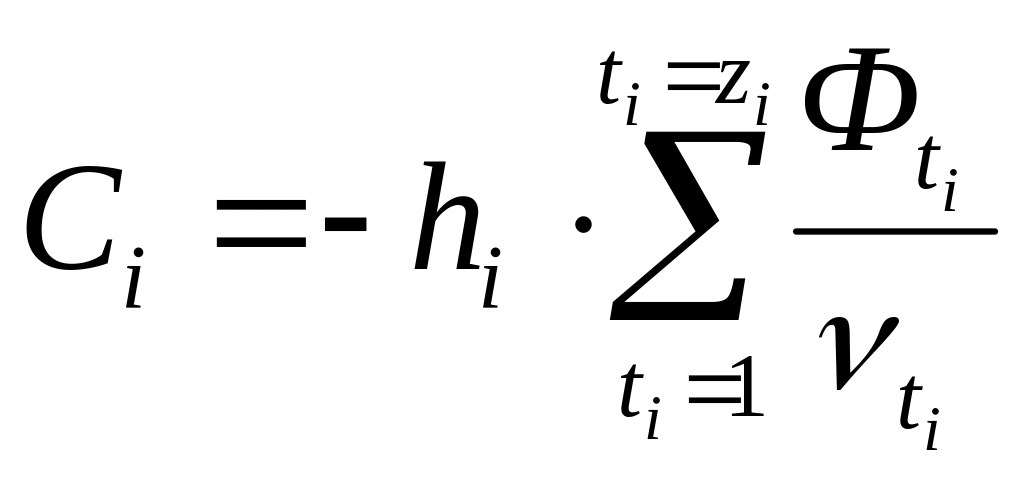, – оптическая сила линзы с номером t i-го компонента, z_i – количество линз в i-м компоненте, – коэффициент дисперсии.

Как и в монохроматических суммах оптическая сила линз і-го компонента нормируют:

, Тогда :

И тогда окончательно первая хроматическая сумма обретет вид:

является неизвестным, которое оттискивают решая уравнение

Хроматизм увеличенияХарактеризуется .Таккак ,то:

Вычисление правой части аберрационных уравнений.

В правой части уравнения выставляется нужное значение суммы Зейделя, здесь возможны два случая:

1) Уравнение составляется для всей системы(в системе отсутствует унифицированные компоненты – призмы, окуляры) тогда в правой части записывается 0.

2) В системе присутствуют призмы окуляры (и которые являются унифицированными). Тогда в правой части записывают некое не нулевое значение суммы, которое позволяет остаточным аберрациям разрабатываемой части системы компенсировать аберрации остальной части системы.

В качестве примера рассмотрим систему зрительной трубы с призменной оборачивающей системой Кеплера.

В этой системе призменная оборачивающая система – унифицированная.

Для анализа остаточных аберраций выделенной части системы ее поворачивают на 180° и запускают в нее луч в прямом направлении

В матрице конструктивных параметров все радиусы, толщины показатели преломления меняются местами, а радиусы еще меняют знак.

Следующий шаг – полный анализ аберраций в выделенной системе путем расчета хода действительных лучей. Для этого используют «OPAL» «ZEMAX» «ЛУЧ».

Используя данные аберрационного анализа вычисляют значения сумм Зейделя тоесть правую часть аберрационного уравнения по формулам:

если предмет на бесконечности

(для значения m, которое подставляется в (1))

m – координата луча на выходном зрачке синтезируемой части в обратном ходе.

m берут для луча идущего по краю зрачка.

s₁ – удаление плоскости предметов, t – удаление входного зрачка в прямом ходе, α₁ – первый угол первого ВНЛ нормированный, f’ – фокусное расстояние синтезируемой системы в прямом ходе, n_p+1 – показатель преломления среды за синтезируемой частью системы.

Вычисляется размер комы:

– неизопланатизм( в таблице аберраций осевого пучка).

Неизопланаизм определяют по краю поля зрения для соответствующего краю поля зрения. – это координата точки пересечения главного луча с плоскостью изображения.

– координата для +m, – координата для –m.

Формула для предмета на конечном расстоянии:

Для бесконечно удаленного:

ω – угловая координата края поля зрения в пространстве предметов системы в прямом ходе.

Примечание: при определении знака ω важно не сделать ошибку проследив ход пучка по которому определялась , в обратном ходе до выхода из всей системы.

– астигматизм

Вычисляется для координаты предметной точки .

вычисляется для .

Данные о располагаются в таблице в программе ОПАЛ «Аберрация главного луча».

– кривизна поля

Характеризуется четвертой суммой

радиус поверхности Пецваля

– дисторсия – это составляющая от дисторсии вычисленная по .

Если предмет на бесконечности

Примечание: при подстановке проследить знак . Он должен соответствовать тому пучку той предметной точки по которой определяется с учетом поворота системы в начальное положение. Значение в таблице «Аберрации главного луча».

– хроматизм положения

при и

– хроматизм увеличения

– координата изображения точки в ПИ,

– поперечный отрезок от хроматизма увеличения,

– инвариант Легранжа-Геймгольца.