12. Вычеты.
Если
ф-ция аналитическая в какой-то конкр.
окрестности z=a,
она может быт разложена в ряд Лорана:
Особую
роль среди коэф-тов играет коэф-т С-1.
Он наз. вычетом ф-ции f(z)
в точке z=a.
.
,
где контур
замкнутый контур, окружающий точку z=a
и положительно ориентированный. В
качестве можно
взят окр. С центром в точке а достаточно
малого радиуса (чтобы контур не содержал
внутри других особых точек).
.
Вычисление вычетов в полюсе.
Пуст
точка z=a
явл. полюсом 1-ого порядка. В этом случае
разложение в ряд Лорана
.
Домножим f(z)
на z-a
.
Переходя к пределу при
,
получим, что
.
.
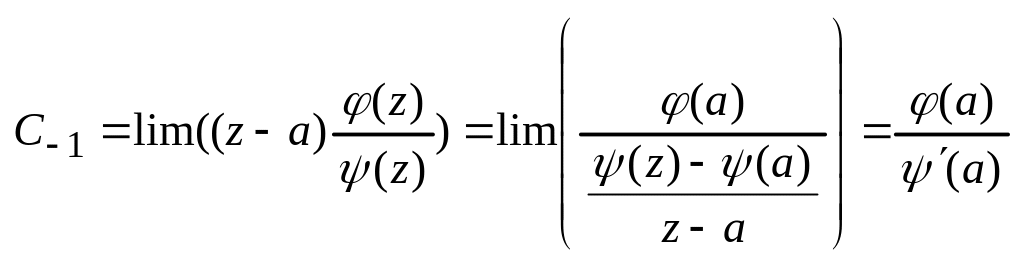
Умножим выражение на (z-a)k
.
Продифференцировать к-1 раз это выражение
и переходя к пределу при
,
получим:
.
13. Основная теорема о вычетах.
Пусть ф-ция f(z) аналитична в некоторой области за исключением крнечного числа особых точек, то согласно теореме (интегр.) Коши для многосвязной области:
.
С другой стороны, если интеграл расписать
как
.
14. Оригиналы и изображения.
Ф-ция
f(t) наз.
ф-цией оригиналом, если они удовлетсв.
след. 3 условиям:
при t<0 { f(0)=f(0+)
}
2)сущесвуют
константы M и S0:
S0=ints
S0 показатель роста ф-ции.
3) на любом промежутке [0;Т] ф-ция должна иметь только конечное число точек разрыва и только 1 рода.
Ф-ция Хевисайда или ф-ция единичного скачка
.
В
дальнейшем под ф-цией f(t)
будем подразумевать произведение этой
ф-ции на ф-цию Хевисайда
.
интеграл Лапласа
(1).
Теорема
о существовании: если f(t)
ф-ция-оригинал, то изображение F(p)
сущ. В полуплоскости
,
а интеграл (1) в этой полуплоскости
сходится абсолютно и равномерно и ф-ция
F(p) явл.
аналитической ф-цией в этой же
полуплоскости.
Док-во: Покажем, что (1) сходиться абсолютно и равномерно в этой полуплоскости.
По признаку Вейер-Штрассе этот интеграл сходится по параметру p, т.е. в этой полуплоскости интеграл сходится абсолютно и равномерно. Нужно показать, что F(p) дифференцируема.
аналогична на
полуплоскости.
15.Теорема о существовании изображения.
Теорема:
если
-функция
оригинал, то изображение
существует
в полуплоскости
,
а интеграл в этой полуплоскости сходится
абсолютно и равномерно и функия
является аналитической ф-цией в этой
же полуплоскости.
Док-во:
Покажем,
что интеграл Лапласа
сходится абсолютно и равномерно в этой
полуплоскости
По
признаку Вейер-Штрассе этот интеграл
сходится по параметру p,
т. е. в этой полуплоскости интеграл
сходится абсолютно и равнометно. Нужно
показать, что
дифференцируема.
;;;
;
отсюда следует, что
аналитична на полуплоскости.
16. Теорема подобия.
Пусть
- оригинал;
для любого
.
Доказательство.
17.Теорема смещения в области аргумента изображения.
Теорема:
умножению оригинала на
соответствует смещение аргумента
изображения на величину
:
Док-во:
.
18.Теорема запаздывания.
Теорема:
если F(p)
есть изображение ф-ии f(t),
то
есть изображение ф-ии f(t-t0),
т. е. если
,
то
.
Док-во:
По
определению изображения имеем:
1-ый
интеграл, стоящий в правой части равенства
равен 0, так как f(t-t0)=0
при t<t0.
В последнем интеграле сделаем замену
переменной: t-t0=z;
.
Таким образом,
.
19.Теорема о дифференцировании оригинала.
Док-во:
;
;
;В
частном случае, когда условие задачи
Коши нулевое, то
.
20. Теорема об интегрировании оригинала
(1)
(2)
К равенству (2) применим преобразование Лапласа
Пример:
=
.
21. Теорема о дифференцировании изображения
Пусть
,
тогда дифференцированию изображения
соответствует умножение оригинала на
(-t)
Поскольку F(p) аналогична, то она и дифференцируема
………………………….…..
.
22. Теорема об интегрировании изображения
интегрированию изображение соответствует деление оригинала на t:
Док-во:
;
;
Пример:
.
23. Теорема об изображении периодического интеграла.
Если
- Т – период оригинала, то
,
где
,
а
Доказательство.
.
И так далее…
24. Свертка функции, ее основные свойства.
Сверткой
двух функций
и
называется несобственный интеграл
,
;
,
,
.
(для функций-
ригиналов).
Свойства свертки:
1)
Коммутативность
2)
Ассоциативность
3)
Линейность
25. Теорема Бореля об умножении изображений (о свертке)
Пусть
функция
- функция оригинал
,
также функция
- функция оригинал
,
тогда
Если вспомнить интеграл Лапласа:
=,
где
Покажем порядок интегрирования, получим
=
.
28. Решение линейных дифференциальных уравнений с постоянными коэффициентами.
Для
ЛНДУ
-го
порядка поставлены условия Коши:
,
,…,
Составим операторное уравнение, соответствующее данному:
…………………
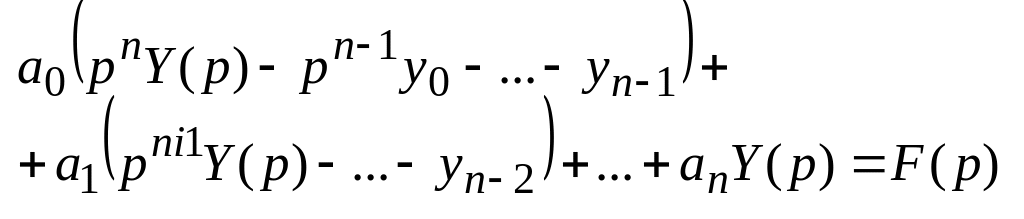- линейное
алгебраическое уравнение относительно
- операторное
уравнение.
- неизвестная
функция.
Замечание. Операционным методом можно найти и общее решение ЛНДУ, для этого нужно поставить следующую задачу Коши.
