20) Внутренняя энергия системы. Внутренняя энергия идеального газа и вычисление её через число степеней свободы. Два способа изменения внутренней энергии. Количество теплоты. Теплоемкость. Связь удельной и молярной теплоемкостей.

Внутренняя энергия – функции состояния системы или вещества. Не зависит от того, каким образом система переходит в это состояние, а зависит только от начального и конечного положения.

Внутренняя энергия системы – полная энергия системы, за вычетом Екин системы в целом и за вычетом потенциальной энергии системы в поле внешних сил.

U=Eполн. - Eвнеш.

U=

Идеальный газ – газ, взаимодействием и размерами которого можно пренебречь. Значит, . Кинетическая энергия движения молекул определяется температурой.

Особенности:

1)Внутренняя энергия системы является функцией состояния и однозначно определяется параметрами системы;

2)Внутренняя энергия – величина аддитивная. Для 1 моль вещества: U=(i/2)*K*T*Na

K*Na=R, U(1 моль)=(i/2)*R*T

При n моль, dU = (i/2)*n*R*dT

dU - Внутренняя энергия, записанная через число степеней свободы.

Внутреннюю энергию можно изменить двумя способами:

1)совершить над системой работу;

2)сообщить ей некоторое количество теплоты.

КОЛИЧЕСТВО ТЕПЛОТЫ

При теплопередаче (теплообмене) внутренняя энергия одних тел уменьшается, а других – увеличивается, без изменения механической энергии тел и без совершения работы. При этом уменьшается внутренняя энергия тела-нагревателя, а внутренняя энергия нагреваемого тела увеличивается .

Процесс теплопередачи характеризуется количеством теплоты.  Количеством теплоты (Q) называется   изменение внутренней энергии тела, происходящее в результате теплопередачи.  Количество теплоты измеряется в системе СИ в джоулях. [Q] = 1Дж. Кроме того,  для измерения количества теплоты (вне системы СИ) используется единица, называемая калорией (кал).  1 калория равна количеству теплоты, необходимому для нагревания 1 г воды на 1 градус С.  Опытным путем было установлено, что для нагревания 1 г воды на 1 градус требуется  совершить работу в 4,18 Дж, следовательно 1кал = 4,18Дж.

Теплоёмкость – величина, которая зависит от вида процесса.

Теплоемкость идеального газа — это отношение количества теплоты, сообщенного газу, к изменению температуры δТ, которое при этом произошло.

Удельная теплоёмкость (Удельная теплота нагревания на один градус, С уд.) вещества - количество тепловой энергии, необходимой для повышения температуры одного килограмма вещества на один градус. (Дж/(кг ·К)). 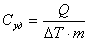где  — удельная теплоёмкость,  — количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении),  — масса нагреваемого (охлаждающегося) вещества,  — разность конечной и начальной температур вещества.

Молярная теплоёмкость (С_μ) — это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры. (Дж/(моль·К)).

.

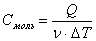Удельная и молярная теплоемкости связаны соотношением: , где М — молярная масса (масса одного моля вещества).

Чаще всего работаем с молярной теплоёмкостью!

21)Работа при изменении объема. Первое начало термодинамики. Формула Майера. Применение первого начала термодинамики к изопроцессам идеального газа.

Работа при изобарном расширении газа. Одним из основных термодинамических процессов, совершающихся в большинстве тепловых машин, является процесс расширения газа с совершением работы. Легко определить работу, совершаемую при изобарном расширении газа.

   Если при изобарном расширении газа от объема V₁ до объема V₂ происходит перемещение поршня в цилиндре на расстояние l (рис. 106), то работа A', совершенная газом, равна

 , (33.1)

где p — давление газа,  — изменение его объема.

Работа при произвольном процессе расширения газа. Произвольный процесс расширения газа от объема V₁ до объема V₂можно представить как совокупность чередующихся изобарных и изохорных процессов. 

   При изохорных процессах работа равна нулю, так как поршень в цилиндре не перемещается. Работа при изобарных процессах пропорциональна площади фигуры на диаграмме p, V под соответствующим участком изобары (рис. 108).

Следовательно, работа при произвольном процессе расширения газа прямо пропорциональна площади фигуры под соответствующим участком графика процесса на диаграмме p, V.

Как видно из рисунка 107, при изображении изобарного процесса расширения газа в координатных осях p , V площадь фигуры, ограниченной графиком процесса, кординатами V₁ и V₂, осью абсцисс, пропорциональна работе газа A'.

Работа при изотермическом расширении газа. Сравнивая площади фигур под участками изотермы и изобары (рис. 109), можно сделать вывод, что расширение газа от объема V₁ до объема V₂ при одинаковом начальном значении давления газа сопровождается в случае изобарного расширения совершением большей работы.

Работа при сжатии газа. При расширении газа направление вектора силы давления газа совпадает с направлением вектора перемещения, поэтому работа A', совершенная газом, положительна (A' > 0), а работа А внешних сил отрицательна: A = -A' < 0.

   При сжатии газа направление вектора внешней силы совпадает с направлением перемещения, поэтому работа А внешних сил положительна (A > 0), а работа A', совершенная газом, отрицательна (A' < 0).

Вывод Формулы Майера

Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V, Р и тому подобных), поэтому формула (4.2.5) справедлива для любого процесса.

Для произвольной идеальной массы газа:

(4.2.6)

При изобарическом процессе, кроме увеличения внутренней энергии, происходит совершение работы газом: (4.2.7)

Из основного уравнения молекулярно-кинетической теории  . При изобарическом процессе Р = const. Следовательно, из (4.2.7) получим: (4.2.8) - Это уравнение Майера для одного моля газа.

Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе.

       Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж.

       Полезно знать формулу Майера для удельных теплоёмкостей:

.

       или

.

Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными.