Бегущая волна

Бегущая волна — волновое движение, при котором поверхность равных фаз (фазовые волновые фронты) перемещается с конечной скоростью (постоянной для однородной среды). С бегущей волной, групповая скорость которой отлична от нуля, связан перенос энергии, импульса или других характеристик процесса^[1].

Бегущая волна - волна, которая при распространении в среде переносит энергию (в отличие от стоячей волны). Примеры: упругая волна в стержне, столбе газа, жидкости, электромагнитная волна вдоль длинной линии, в волноводе^[2].

Бегущая волна — волновое возмущение, изменяющееся во времени   и пространстве   согласно выражению

где   — амплитудная огибающая волны,   — волновое число и   — фаза колебаний. Фазовая скорость   этой волны даётся выражением

где   — это длина волны.

Вывод уравнения бегущей волны

Рассмотрим колебания источника волны, происходящие с циклической частотой ω   и амплитудой A:

где x(t) — смещение источника от положения равновесия.

В некоторую точку среды колебания придут не мгновенно, а через промежуток времени, определяемый скоростью волны и расстоянием от источника до точки наблюдения. Если скорость волны в данной среде равна υ, то зависимость от времени t координаты (смещение) x колеблющейся точки, находящейся на расстоянии r от источника, описывается уравнением

где k —волновое число   — фаза волны.

Выражение (1) называется уравнением бегущей волны.

Бегущую волну можно наблюдать при следующем эксперименте: если один конец резинового шнура, лежащего на гладком горизонтальном столе, закрепить и, слегка натянув шнур рукой, привести его второй конец в колебательное движение в направлении, перпендикулярном шнуру, то по нему побежит волна.

16)Образование стоячих волн. Уравнение стоячей волны. Амплитуда стоячей волны. Координаты узлов и пучностей стоячей волны. (Савельев и.В. Т.2 § 99, методичка №81, работа №7)

Стоячие волны - Волны, образующиеся при наложении двух бегущих волн, распростра­няющихся навстречу друг другу с одинаковыми частотами и амплитудами.

Уравнение стоячей волны

Складываем волны

и

S=

(учли, что k = 2π/λ)—уравнение стоячей волны.

Образование стоячих волн наблюдают при:

Интерференции бегущей и отраженной волн. Например, если конец веревки закрепить неподвижно, то отраженная в месте закрепления веревки волна будет интерферировать с бегущей волной и образует стоячую волну. На границе, где происходит отражение волны, в данном случае получается узел. Будет ли на границе отражения узел или пучность, зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, менее плотная, то в месте отражения получается пучность, если более плотная — узел. Образование узла связано с тем, что волна, отражаясь от более плотной среды, меняет фазу на противоположную и у границы происходит сложение колебаний противоположных направлений, в результате чего получается узел. Если волна отражается от менее плотной среды, то изменения фазы не происходит и у границы колебания складываются с одинаковыми фазами — получается пучность

17)Два подхода к изучению макросистем: молекулярно-кинетический и термодинамический. Основные параметры макросистем. Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева). (Савельев И.В. Т.1 § 79–81, 86).

Уравнение состояния идеального газа (уравнение Клапейрона или уравнение Менделеева — Клапейрона)

где

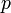•  — давление,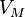

•  — молярный объём,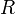

•  — универсальная газовая постоянная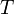

•  — абсолютная температура, К.

Так как , где  — количество вещества, а , где  — масса,  — молярная масса, уравнение состояния можно записать:

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

 — закон Бойля — Мариотта.

 — Закон Гей-Люссака.

 — закон Шарля (второй закон Гей-Люссака, 1808 г.)

А в форме пропорции этот закон удобен для расчёта перевода газа из одного состояния в другое.

Универсальная газовая постоянная (физический смысл) —величина численно равна работе, которую необходимо совершить, чтобы нагреть 1 моль вещества на 1 К при постоянном давлении.

В Международной системе единиц (СИ) универсальная газовая постоянная равна 8,31441 Дж/(моль*К)

Постоянная Больцмана ( или ) — физическая постоянная, определяющая связь между температурой и энергией.

Дж/К

Универсальная газовая постоянная определяется как произведение постоянной Больцмана на число Авогадро, .

18)Основное уравнение молекулярно-кинетической теории.

Основное уравнение молекулярно-кинетической теории идеального газа устанавливает связь между макроскопической величиной - давлением, которое может быть измерено, например манометром, и микроскопическими величинами, характеризующими молекулу:

где р - давление, m₀- масса молекулы, п - концентрация (число молекул в единице объема), v² - средний квадрат скорости молекул.

Если через Е обозначить среднюю кинетическую энергию поступательного движения молекулы

можно записать:

Давление идеального газа пропорционально концентрации молекул и средней кинетической энергии их поступательного движения.

19)Уравнение состояния реального газа (уравнение Ван-дер-Ваальса). Теоретическая изотерма Ван-дер-Ваальса и экспериментальная изотерма реального газа. Критическое состояние вещества. (Савельев И.В. Т.1 § 91, § 123–124).

Уравнение состояния реального газа (уравнение Ван-дер-Ваальса)