1.Определение эконометрики. Название “эконометрика” было введено в 1926 году Рагнаром Фришем. В буквальном переводе этот термин означает “измерения в экономике”.

Эконометрика - это самостоятельная научная дисциплина, объединяющая совокупность теоретических результатов, приёмов, методов и моделей, предназначенных для того, чтобы на базе (I) экономической теории, (II) экономической статистики, (III) математико-статистического инструментария придавать конкретные количественные выражения общим (качественным) закономерностям, обусловленным экономической теорией.

Таким образом, эконометрика занимается эмпирическим выводом экономических законов. Эконометрика также формулирует экономические модели, основываясь на экономической теории или на эмпирических данных, оценивает неизвестные величины (параметры) в этих моделях, делает прогнозы (и оценивает их точность) и даёт рекомендации по экономической политике.

2.Взаимосвязь эконометрики с другими дисциплинами». Эконометрика (или эконометрия) входит в обширное семейство дисциплин, посвященных измерениям и применению статистических методов в различных областях науки и практики. Эконометрика — это не тоже самое, что экономическая статистика. Она на идентична и экономической теории, хотя значительная часть этой теории носит количественный характер.Экономическая теория — дисциплина экономической науки. Представляет собой теоретическое и философское основание экономической науки. Состоит из множества школ и направлений. Экономическая теория не стоит на месте и её развитием в исторической ретроспективе занимается история экономических учений.

Основная задача экономической теории — дать объяснения происходящих событий в экономической жизни с помощью моделей действительности, отразить в себе реальную экономику.

Экономическая теория состоит из ряда разделов: методологии экономической науки, микроэкономики, макроэкономики, международной экономики, эконометрики, теории игр.

В современной экономической теории можно выделить ряд научных школ и направлений: неокейнсианство, монетаризм, новую институциональную экономическую теорию, нейроэкономику, австрийскую школу, новую политическую экономию, экономику и право.

3.Методология построения экономических моделей

Задача эк-ки- построение моделей эк явлений и исп-е этих моделей д/опис-для, анализа и прогнозир-я. В действит-ти модели н. д/упр-я и д/принятия управленч. реш-й. Своеобразие Э.-примен-е методов точных наук к опис-ю деят-ти чела, т.е. к гум. наукам. Гл. метод в эк-ке – это регрессионный анализ, т.е. построение Ур-я связи по фактич. данным, по больш. наборам чисел. В эк-ке выделяют 3 раздела: регрессия (ур-е регресии), врем. ряды (регрессия, аргументом явл. вр.), с-мы ур-й. предназн-е. Эконометрика также формулирует экономические модели, основываясь на экономической теории или на эмпирических данных, оценивает неизвестные величины (параметры) в этих моделях, делает прогнозы (и оценивает их точность) и даёт рекомендации по экономической политике.

4.Область применения эконометрических моделей

Представляется система эконометрических моделей, предназначенная для прогнозирования целевых показателей и оценки вариантов денежно-кредитной политики. Эконометрические модели в форме коррекции ошибок, интегрированные в данную систему, взаимосвязаны по переменным, выступающим в роли инструментов денежно- кредитной политики, по общим экзогенным переменным, характеризующим внешние воздействия, а также по эндогенным переменным, выступающим в качестве целевых показателей денежно-кредитной политики. Описываются результаты оценки точности прогнозов и анализа вариантов денежно-кредитной политики на основе предлагаемой системы.

5.Понятие о функциональной, статистической и корреляционной связях.

Различают два типа связей между различными явлениями и их признаками: функциональную или жестко детерминированную, с одной стороны, и статистическую или стохастически детерминированную- с другой. Строго определить различие этих типов связи можно тогда, когда они получают математическую формулировку. Для простоты будем говорить о связи двух явлений или двух признаков, математически отображаемой в форме уравнения связи двух переменных.

Если с изменением значения одной из переменных вторая изменяется строго определенным образом, т.е. значению одной переменной обязательно соответствует одно или несколько точно заданных значений другой переменной, связь между ними является функциональной.

Нередко говорят о строгом соответствии лишь одного значения второй из переменных каждому значению первой из них, но это неверно. Например, связь между у и х является строго функциональной, если , но значению х = 4 соответствует не одно, а два значения: у1 = +2; у2 = - 2. Уравнения более высоких степеней могут иметь несколько корней, связь, разумеется, остается функциональной.

Функциональная связь двух величин возможна лишь при условии, что вторая из них зависит только от первой и ни от чего более. В реальной природе (и тем более в обществе) таких связей нет; они являются лишь абстракциями, полезными и необходимыми при анализе явлений, но упрощающими реальность. Функциональная зависимость данной величины у от многих факторов х1, х2, ..., хn возможна только в том случае, если величина y всегда зависит только от перечисленного набора факторов x1, х2 ..., хk и ни от чего более.

6. Основные задачи прикладного корреляционно-регрессионного анализа.

Основными задачами корреляционного анализа являются оценка силы связи и проверка статистических гипотез о наличии и силе корреляционной связи. Не все факторы, влияющие на экономические процессы, являются случайными величинами, поэтому при анализе экономических явлений обычно рассматриваются связи между случайными и неслучайными величинами. Такие связи называются регрессионными, а метод математической статистики, их изучающий, называется регрессионным анализом.

Использование возможностей современной вычислительной техники, оснащенной пакетами программ машинной обработки статистической информации на ЭВМ, делает практически осуществимым оперативное решение задач изучения взаимосвязи показателей биржевых ставок методами корреляционно-регрессионного анализа.

При машинной обработке исходной информации на ЭВМ, оснащенных пакетами стандартных программ ведения анализов, вычисление параметров применяемых математических функций является быстро выполняемой счетной операцией.

7.Уравнение регрессии, его смысл и назначение Смысл регрессионного анализа – построение функциональных зависимостей между двумя группами переменных величин Х₁, Х₂, … Х_р и Y. При этом речь идет о влиянии переменных Х (это будут аргументы функций) на значения переменной Y (значение функции). Переменные Х мы будем называть факторами, а Y – откликом.

Сегодня мы разберем наиболее простой случай – установление зависимости одного отклика y от одного фактора х. Такой случай называется парной (простой) регрессией.

8. Выбор типа матем-й функции при построении уравнения регрессии Построение модели

Исходные данные: заранее известные (экспериментальные, наблюденные) значения фактора х_i – экзогенная переменная и соответствующие им значения отклика y_i, (i = 1,…,n) - эндогенная переменная;

Активный и пассивный эксперимент.

Выборочные характеристики – позволяют кратко охарактеризовать выборку, т. е., получить ее модель, хотя и очень грубую:

а) среднее арифметическое:

Среднее арифметическое – это «центр», вокруг которого колеблются значения случайной величины.

Основные этапы построения эконометрических моделей

На первом постановочном этапе построения эконометрической модели формируются цели моделирования, определяется набор участвующих в модели факторов, т.е. устанавливается, какие из переменных будут рассматриваться как экзогенные, а какие как эндогенные и лаговые.

Пусть У ={у1 у2 …уm}, множество эндогенных переменных ; Х = {х1 х2 …хm} – множество экзогенных переменных.

Задачей экзогенного моделирования является получение каждой эндогенной переменной от совокупности экзогенных переменных и возможно от части эндогенных.

y1 = f (x1 … xk у2 … уm)

При этом зависимые переменных лаговые.

На 1 ом этапе осуществляется анализ экономической сущности изучаемой модели.

На 3 ем этапе выбор общего вида модели: парная, множественная; сколько должно войти факторов; линейная не линейная; а так же определение коэффициентов функции f.

4 ый этап отбор необходимой статистической информации и предварительный анализ данных.

5 ый этап – идентификация модели, т.е. стат анализ модели, стат оценка независимых параметров модели. Наиболее часто для оценки (нахождения) параметров модели применяют метод наименьших квадратов (МНК)

6 ой этап – сопоставление реальных и модельных значений. Иначе оценка адекватности и точности модели.

9. Парной регрессией называется уравнение связи двух переменных у и х

Вида y = f (x),

где у – зависимая переменная (результативный признак);

х – независимая, объясняющая переменная (признак-фактор).

Различают линейные и нелинейные регрессии.

Метод наименьших квадратов МНК

Для оценки параметров регрессий, линейных по этим параметрам, используется метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических значений ŷx при тех же значениях фактора x минимальна, т. е.

10. .Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.

Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.

Пусть дано решить систему уравнений

a₁x + b₁y + c₁z + … + n₁ = 0

a₂x + b₂y + c₂z + … + n₂ = 0 (1)

a₃x + b₃y + c₃z + … + n₃ = 0

…

число которых более числа неизвестных x, у, z… Чтобы решить их по способу Н. квадратов, составляют новую систему уравнений, число которых равно числу неизвестных и которые затем решаются по обыкновенным правилам алгебры. Эти новые, или так называемые нормальные, уравнения составляются по следующему правилу: умножают сперва все данные уравнения на коэффициенты у первой неизвестной х и, сложив почленно, получают первое нормальное уравнение, умножают все данные уравнения на коэффициенты у второй неизвестной у и, сложив почленно, получают второе нормальное уравнение и т. д. Если означить для краткости:

[aa] = a₁a₁ + a₂a₂ +…

[ab] = a₁b₁ + a₂b₂ +…

[ac] = a₁c₁ + a₂c₂ +…

…

[ba] = b₁a₁ + b₂a₂ +…

[bb] = b₁b₁ + b₂b₂ +…

[bc] = b₁c₁ + b₂c₂ +…

…

то нормальные уравнения представятся в следующем простом виде:

[aa]x + [ab]y + [ac]z + … + [an] = 0

[ba]x + [bb]y + [bc]z + … + [bn] = 0 (2)

[ca]x + [cb]y + [cc]z + … + [cn] = 0

11. Оценка тесноты связи

12. Коэффициент ковариации

М_ч(у) - Т.е. получим корреляционную зависимость.

Наличие корреляционной зависимости не может ответить на вопрос о причине связи. Корреляция устанавливает лишь меру этой связи, т.е. меру согласованного варьирования.

Меру взаимосвязи м\у 2 мя переменными можно найти с помощью ковариации.

, ,

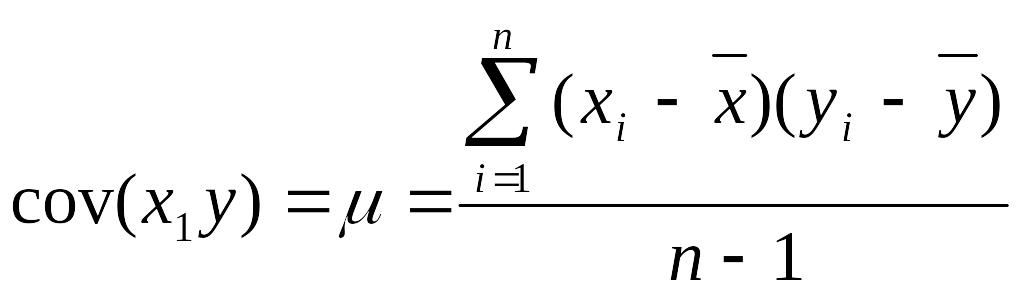Величина показателя ковариации зависит от единиц в γ измеряется переменная. Поэтому для оценки степени согласованного варьирования используют коэффициент корреляции – безразмерную характеристику имеющую определенный пределы варьирования..

13.Показатели корреляции: линейный коэффициент. индекс корреляции. Наиболее распространенный коэффициент корреляции. Предназначен для расчета силы и направления линейной зависимости между переменными исследования.

Смысл коэффициента линейной корреляции.

Коэффициент линейной корреляции отражает меру линейной зависимости между двумя переменными. Предполагается, что переменные измерены в интервальной шкале либо в шкале отношений.Если представить две переменные на координатном поле , то каждая пара значений будет отображать координаты точки в этом поле. Чем ближе точки к усредненной прямой, тем выше коэффициент корреляции Коэффициент корреляции будет положительным числом, когда при повышении X происходит повышение Y (прямопропорциональная связь), отрицательным при обратнопропорциональной связи. На иллюстрации изображены различные по силе положительные коэффициенты корреляции. Индекс корреляции используется для выявления тесноты связи между переменными в случае нелинейной зависимости.

Он показывает тесноту связи между фактором x и зависимой переменной y: . (6.13)

где ei = yi - i - величина ошибки, т.е. отклонение фактических значений зависимой переменной от рассчитанных по уравнению регрессии.

Индекс корреляции есть неотрицательная величина, не превосходящая 1: 0 ≤ Iyx ≤ 1.

Связь тем сильнее, чем ближе Iyx к единице.

В случае линейной зависимости Iyx = | ryx |. Расхождение между Iyx (формула (6.13)) и ryx (формула (6.4)) может быть использовано для проверки линейности корреляционной зависимости.