21.2. Уравнения Лагранжа второго рода
Уравнения
Лагранжа второго рода – это дифференциальные
уравнения движения механической системы
в обобщенных координатах.
Для
получения уравнений движения воспользуемся
общим уравнением динамики: 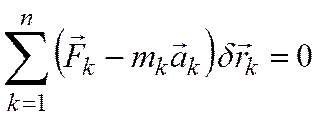 .
.
Для
системы со стационарными связями
виртуальное перемещение  -й точки выражается,
как было показано раньше, через обобщенные
координаты соотношением
-й точки выражается,
как было показано раньше, через обобщенные
координаты соотношением  .
.
Подстановка
его в общее уравнение динамики дает:
 .
.
Перегруппируем
слагаемые, меняя порядок суммирования,
 .
.
Так
как связи голономные, то вариации
обобщенных координат  независимы.
Следовательно, коэффициенты при вариациях
обобщенных координат равны нулю.
независимы.
Следовательно, коэффициенты при вариациях
обобщенных координат равны нулю.
То
есть 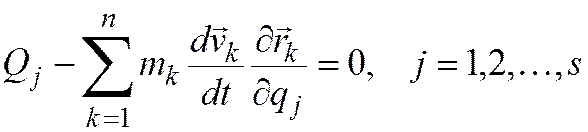 . (21.1) Так
как
. (21.1) Так
как  , то
с учетом тождеств Лагранжа
имеем:
, то
с учетом тождеств Лагранжа
имеем:  .
(21.2)
.
(21.2)
Подставляя соотношение
(21.2) в равенство (21.1), внося  под
знаки производных и меняя порядок
суммирования и дифференцирования,
получаем
под
знаки производных и меняя порядок
суммирования и дифференцирования,
получаем

 или
или



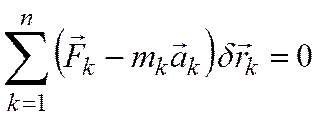 .
. .
.  .
. .
.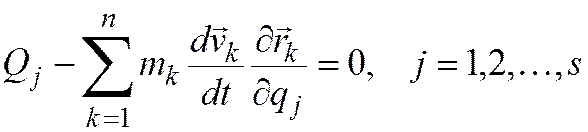 . (21.1) Так
как
. (21.1) Так
как  , то
с учетом тождеств Лагранжа
имеем:
, то
с учетом тождеств Лагранжа
имеем:  .
(21.2)
.
(21.2)
