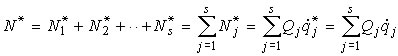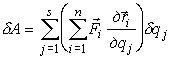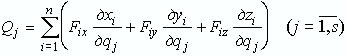6.2.4. Применение принципа возможных перемещений для определения опорных реакций

 

Согласно принципу освобождаемости от связей равновесие системы не нарушится, если какую-либо связь системы исключить, а действие связи заменить силой реакции.

Поэтому для определения реакций в какой-либо связи надо эту связь отбросить, а вместо нее на расчетной схеме показать силу реакции, которую в дальнейшем надо считать активной силой.

В результате отбрасывания связи система, находившаяся до этого в равновесии, приобретает дополнительную степень свободы. Далее, применяя принцип возможных перемещений в последовательности, указанной в п. 6.2.2, можно получить уравнение, из которого определяется искомая реакция связи.

ВОПРОС 17 

Формулировка принципа: при движении механической системы с идеальными связями сумма работ всех активных сил и сил инерции на любом возможном перемещении равна нулю.

Это положение носит также название общего уравнения динамики системы.

Как и принцип возможных перемещений, общее уравнение динамики может быть записано в различных формах:

;            (6.11)

;             (6.12)

                              (6.13)

 

Общее уравнение динамики дает универсальный метод исследования движения механических систем.

ВОПРОС 18

ОБОБЩЕННЫЕ КООРДИНАТЫ

независимые между собой параметры qi (r = 1, 2,..., s) любой размерности, число которых равно числу s степеней свободы механич. системы и которые однозначно определяют положение системы.

Любые s величин q1, q2, ..., qs, вполне характеризующие положение системы (с s степенями свободы), называют ее обобщенными координатами, а производные  i — ее обобщенными скоростями.

Обобщенные силы. Способы вычисления обобщенных сил.

В аналитической механике наряду с понятием о силе как векторной величине, характеризующей воздействие на данное тело со стороны других материальных тел, используют понятие об обобщенной силе. Для определения обобщенной силы рассмотрим возможную работу сил, приложенных к точкам системы,

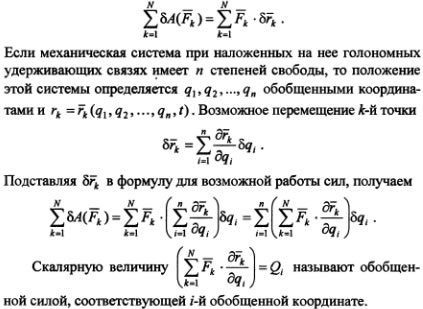
Таким образом, обобщенной силой, соответствующей i-й обобщенной координате, называется величина, равная коэффициенту при вариации данной обобщенной координаты в выражении возможной работы сил, действующих на механическую систему.

В общем случае обобщенная сила является функцией обобщенных координат, скоростей точек системы и времени. Из определения следует, что обобщенная сила — скалярная величина, которая зависит от выбранных для данной механической системы обобщенных координат. Это значит, что при изменении набора обобщенных координат, определяющих положение данной системы, изменятся и обобщенные силы.

Рассмотрим основные способы вычисления обобщенных сил.

Первый способ аналогичен тому, что мы применяли для вычисления виртуальной работы сил системы в обобщенных координатах.

Второй способ используется для голономных систем со стационарными связями, когда обобщенные скорости могут совпадать с виртуальными обобщенными скоростями, то есть

(7)

Третий способ основан на выражении обобщенных сил в координатной форме.

(8)

выразим обобщенную силу по соответствующей обобщенной координате как

(9)

Выразив (9) в аналитической форме записи, получаем формулу для вычисления обобщенных сил в координатной форме:

(10)

где Fix, Fiy, Fiz - проекции силы Fi на оси координат.

Четвертый способ применяется тогда, когда большинство сил системы потенциальны.