14) Теорема об изменении кинетической энергии системы.

Если рассмотреть какую-нибудь точку системы с мас­сой , имеющую скорость , то для этой точки будет

,

где и - элементарные работы действующих на точку внеш­них и внутренних сил. Составляя такие уравнения для каждой из точек системы и складывая их почленно, получим

,

или

. (2)

Равенство выражает теорему об изменении кине­тической энергии системы в дифференциальной форме.

Проинтегрировав обе части равенства (2) в пределах, соответствующих перемещению системы из некоторого начального положения, где кинетическая энергия равна , в положение, где значение кинетической энергии становится равным , будем иметь

.

Полученное уравнение выражает теорему об изменении кинетической энергии в конечном виде: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом пере­мещении всех приложенных к системе внешних и внутренних сил.

Рассмотрим два важных частных случая.

1) Неизменяемая система. Неизменяемой будем называть систему, в которой расстояния между точками приложения внутрен­них сил при движении системы не изменяются. В частности, такой системой является абсолютно твердое тело или нерастяжимая нить.

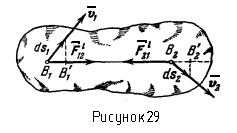
Рис.51

Пусть две точки и неизменяе­мой системы (pис.51), действующие друг на друга с силами и ( ) имеют в данный момент скорости и . Тогда за промежу­ток времени dt эти точки совершат элементарные перемещения и , направленные вдоль векторов и . Но так как отрезок является неизменяемым, то по известной теореме кинематики про­екции векторов и ,а, следовательно, и перемещений и на направление отрезка будут равны друг другу, т.е. . Тогда элементарные работы сил и будут одинаковы по мо­дулю и противоположны по знаку и в сумме дадут нуль. Этот резуль­тат справедлив для всех внутренних сил при любом перемещении системы.

Отсюда заключаем, что для неизменяемой системы сумма работ всех внутренних сил равна нулю и уравнения принимают вид

или .

15)

Вопрос 16

6.2.2)Формулировка принципа: для равновесия механических систем с идеальными стационарными связями необходимо и достаточно, чтобы сумма элементарных работ всех активных сил системы на любом возможном перемещении была равна нулю.

При использовании различных способов вычисления элементарной работы уравнение, выражающее принцип возможных перемещений, может быть записано в следующих формах:

                                      (6.8)

                         (6.9)

Если на систему действуют пары сил с моментами  , то уравнение принципа записывается в форме

                                        (6.10)

где знак “плюс” или “минус” принимается согласно указаниям к формуле (3.7).

Связи системы называются идеальными, если сумма работ всех сил реакции на любом возможном перемещении равна нулю. Примерами идеальных связей являются: гладкая поверхность при скольжении по ней твердого тела, абсолютно шероховатая поверхность при качении тела, шарниры без трения и т. п.

Принцип возможных перемещений используется для исследования состояний равновесия механических систем. Если система имеет одну степень свободы, для нее можно составить одно уравнение, выражающее принцип возможных перемещений; если же система имеет две (или более) степени свободы, то для нее можно соответственно составить два (или более) уравнения, выражающих этот принцип.