10) 1)Моментом инерции твердого тела относительно оси называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до оси.

Моментом инерции твёрдого тела относительно плоскости называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояний от этой точки до плоскости.

Моментом инерции твёрдого тела относительно полюса (полярным моментом инерции) называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от точки до этого полюса.Радиусом инерции тела относительно данной оси z называется линейная величина , определяемая равенством , где М- масса системы.

Момент инерции твёрдого тела относительно некоторой оси равен моменту инерции тела относительно параллельной оси, проходящей через его центр масс, сложенному с произведением массы тела на квадрат расстояния между осями.Допустим, что задана ось. Для доказательства теоремы проведём 3 взаимно перпендикулярные оси, из которых ось  параллельна заданной оси , а ось  лежит в плоскости параллельных осей  и . Для вычисления моментов инерции тела относительно осей  и  опустим из каждой точки  рассматриваемого тела перпендикуляры  и  на оси  и . Выразим длины этих перпендикуляров через координаты этих точек: , (зависимость а). Определим моменты инерции тела относительно осей  и : , . Применим зависимость а)  (зависимость б),  из этой формулы получим  т.к. =0 , то . Подставляя это значение в равенство б), получаем зависимость, установленную теоремой.

Осевые моменты инерции некоторых тел

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения
Тело	Описание	Положение оси a	Момент инерции Ja
	Материальная точка массы m	На расстоянии r от точки, неподвижная
	Полый тонкостенный цилиндр или кольцо радиуса r и массы m	Ось цилиндра
	Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра
	Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1	Ось цилиндра
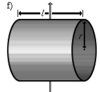
	Сплошной цилиндр длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс
	Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец
	Тонкостенная сфера радиуса r и массы m	Ось проходит через центр сферы
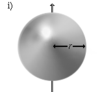
	Шар радиуса r и массы m	Ось проходит через центр шара
	Конус радиуса r и массы m	Ось конуса
	Равнобедренный треугольник с высотой h, основанием a и массой m	Ось перпендикулярна плоскости треугольника и проходит через вершину
	Правильный треугольник со стороной a и массой m	Ось перпендикулярна плоскости треугольника и проходит через центр масс
	Квадрат со стороной a и массой m	Ось перпендикулярна плоскости квадрата и проходит через центр масс

11) Дифф-ные ур-ния вращения твердого тела вокруг неподвижной оси:   ,

Jz – момент инерции тела относительно оси вращения z,  – момент внешних сил относительно оси вращения (вращающий момент).    ,   e – угловое ускорение, чем больше момент инерции при данном  , тем меньше ускорение, т.е момент инерции при вращательном движении является аналогом массы при поступательном. 

12) Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

1. Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости дви­жения центра масс. То есть, для любой точки 

или

2. Вращательное движение. Если тело вращается вокруг какой-нибудь оси Оz (см. рис.46), то скорость любой его точки  , где  - расстояние точки от оси вращения, а w- угло­вая скорость тела. Подставляя это значение и вынося общие множители за скобку, получим:

3. Плоскопараллельное движение. При этом движе­нии скорости всех точек тела в каждый момент времени распреде­лены так, как если бы тело вращалось вокруг оси, перпендикулярной к плоскости движения и проходящей через мгновенный центр ско­ростей Р (рис.46). Следовательно

, 

Работа и мощность сил, приложенных к твёрдому телу, вращающемуся вокруг неподвижной оси.

1)Механической системой или системой материальных точек называется такая их совокупность, при которой изменение положения одной из точек вызывает изменение положения всех остальных.

элементарная работа силы    . Элементарная работа всех сил, приложенных к твёрдому телу  , где   - Главный момент внешних сил относительно оси вращения z. Таким образом   , т.е. элементарная работа сил, приложенных к твёрдому телу, вращающемуся вокруг неподвижной оси, равна произведению главного момента внешних сил относительно оси вращения на приращение угла поворота. Мощность вычисляется по следующей формуле: 

13)

Принцип Даламбера применяется для решения задач динамики несвободных механических систем.

Формулировка принципа: если к каждой точке несвободной механической системы помимо действующих активных сил и сил реакций приложить условную силу инерции, то образованная система сил будет уравновешенной.

Принцип Даламбера позволяет уравнениям динамики придать форму уравнений равновесия статики.

Уравнения принципа Даламбера для конкретной системы зависят от того, как расположены приложенные к этой системе силы ( активные, силы реакции и силы инерции ).

уравнения принципа Даламбера имеют вид:

● если все силы сходятся в одной точке

,

,                                   (5.1)

;

● если силы произвольно расположены в одной плоскости

,

,                                     (5.2)

;

● если силы расположены в произвольной пространственной системе

,

,

,                                 (5.3)

,                     

,

,

где  – активная сила, приложенная к -й точке;  – сила реакции, приложенная к -й точке;  – сила инерции, приложенная к -й точке.

Уравнения принципа Даламбера, как и уравнения статики, могут быть составлены для любых точки и твердого тела, входящих в механическую систему, а также для системы в целом, т. е. как и в статике уравнения принципа Даламбера составляются для выбранного объекта.

Главный вектор и главный момент сил инерции.

Из первого уравнения в (6) следует, что Ф = -(Fe + Re). Но по теореме о движении центра масс главный вектор внешних сил системы (Fe + Re) равен MaC, поэтому

(8)

где aC - ускорение центра масс системы в инерциальной системе координат, принимаемой за неподвижную, или абсолютное ускорение центра масс.

То есть главный вектор сил инерции системы материальных точек равен массе системы, умноженной на величину абсолютного ускорения центра масс, и направлен противоположно этому ускорению.

Из второго уравнения в (6) находим, что главный момент сил инерции относительно произвольного центра O равен MO(Фi) = -(MO(Fie) + MO(Rie)).

Если центр O неподвижен, то согласно теореме об изменении момента количеств движения относительно неподвижного центра MO(Fie) + MO(Rie) = dKO / dt. Поэтому

(9)

то есть главный момент сил инерции системы относительно неподвижного центра O равен взятой со знаком минус производной по времени от момента количеств движения системы относительно того же центра.

Соответственно, главный момент сил инерции относительно неподвижной оси, например оси z, равен

(10)

Если центр подвижен, то согласно той же теореме, но уже относительно подвижного центра A,

(11)

где KA - момент количеств движения системы в абсолютном движении относительно подвижного центра A.

Если подвижный центр совпадает с центром масс C системы материальных точек и VA = VC, то из (11) следует, что

(12)

где KC - момент количеств движения системы относительно центра масс в абсолютном движении.

Учитывая, что момент количеств движения системы относительно цен-тра масс в абсолютном и относительном движении одинаковы, из (12) получаем

(13)

где K rC - момент количеств движения системы в ее относительном движении вокруг центра масс.

Таким образом, из формул (12) и (13) следует, что главный момент сил инерции системы относительно ее центра масс равен взятой со знаком минус производной по времени от момента количеств движения системы относительно центра масс, вычисленного в абсолютном или относительном движении.