Лекция 6. Состояния воздуха и процессы на «I, d» – диаграмме влажного воздуха

Л.К.Рамзин построил «i, d» – диаграмму, которая широко используется в расчетах сушки, кондиционирования воздуха в ряде других расчетов, связанных с изменением состояния влажного воздуха. Эта диаграмма выражает графическую зависимость основных параметров воздуха (t, φ, p_п, d, i) при заданном барометрическом давлении.

Элементы «i, d» – диаграммы показаны на рис. 7.4. Диаграмма построена в косоугольной системе координат с углом между осями i и d 135. По оси ординат откладываются величины энтальпий и температур воздуха (i, кДж/кг сухого воздуха и t, С), по оси абсцисс – величины влагосодержаний влажного воздуха d, г/кг.

Ранее уже упоминалось, что параметры (t C, i кДж/кг, φ %, d г/кг, p_П Па), определяющие состояние влажного воздуха, на «i, d» – диаграмме можно графически изобразить точкой. Например, на рис. ниже точке А соответствуют параметры влажного воздуха: температура t = 27 С, относительная влажность φ = 35 %, энтальпия i = 48 кДж/кг, влагосодержание d = 8 г/кг, парциальное давление пара p_П = 1,24 кПа.

Необходимо учитывать тот факт, что полученные графическим путем параметры влажного воздуха соответствуют барометрическому (атмосферному) давлению 760 мм рт. ст., для которого была построена приведенная на рис. «i, d» – диаграмма.

Практика использования графоаналитических расчетов для определения парциального давления пара с помощью «i, d» – диаграмм показывает, что расхождения между полученными результатами (в пределах 1 - 2 %) объясняется степенью точности построения диаграмм.

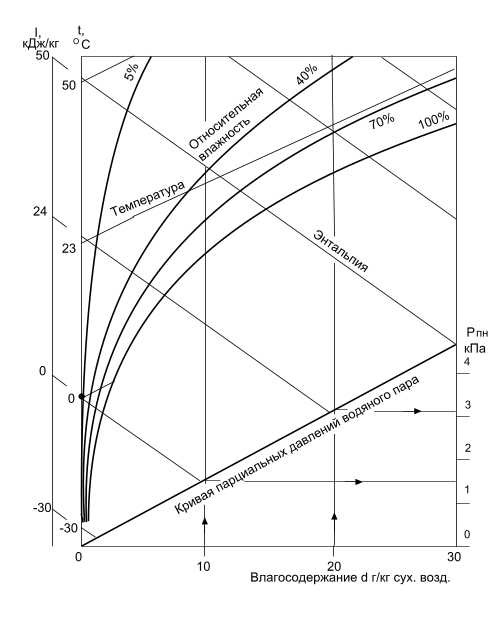
Рис. 7.4. Примерная «i, d» – диаграмма

Если параметры точки А на «i, d» – диаграмме (рис. 7.5) i_А,d_А, а конечного Б – i_Б , d_Б , то отношение (i_Б – i_А) / (d_Б – d_А) · 1000 = ε представляет собой угловой коэффициент линии (луча), характеризующий данное изменение состояния воздуха в координатах «i, d» – диаграммы.

Величина ε имеет размерность кДж/кг влаги. С другой стороны, в практике использования «i, d» – диаграмм заранее известна полученная расчетным путем величина ε.

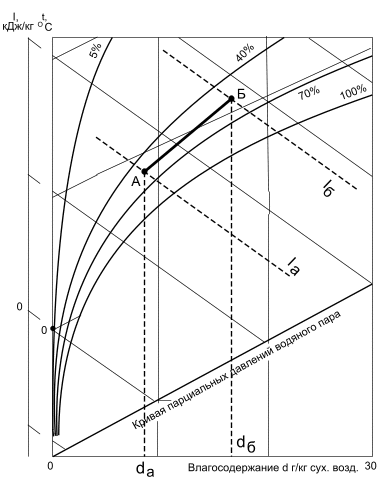
Рис. 7.5. Определение углового коэффициента ε с использованием «i, d» – диаграммы.

В таком случае на «i, d» – диаграмме можно построить луч, соответ-ствующий полученному значению ε. Для этого используют набор лучей, соответствующих различным значениям углового коэффициента и нанесенных по контуру «i, d» – диаграммы. Построение этих лучей производилось следующим образом (см. рис. 7.6).

Для построения углового масштаба рассматривают различные изменения состояния влажного воздуха, приняв при этом одинаковые начальные параметры воздуха для всех рассматриваемых на рисунке 4 случаев – это начало координат (i₁ = 0, d₁ = 0). Если конечные параметры обозначить через i₂ и d₂, то выражение углового коэффициента можно записать в этом случае

ε = .

Например, принимая d₂ = 10 г/кг и i₂ = 1 кДж/кг (соответствует точке 1 на рис. 1.4), ε = (1/10)·1000 = 100 кДж/кг. Для точки 2 ε = 200 кДж/кг и так далее для всех рассматриваемых точек на рисунке 1.4. Для i = 0 ε = 0, т.е. лучи на «i ,d» – диаграмме совпадают. Аналогичным путем могут быть нанесены лучи, имеющие отри-цательные значения угловых коэффициентов.

На полях «i,d» – диаграммы нанесены направления масштабных лучей для значений угловых коэффициентов в пределах от – 30000 до + 30000 кДж/кг влаги. Все эти лучи исходят из начала координат.

Практическое использование углового масштаба сводится к параллельному переносу (например, с помощью линейки) масштабного луча с известным значением углового коэффициента в заданную точку на «i,d» – диаграмме. На рис. показан перенос луча с ε = 100 в точку Б.

Определение температуры точки росы t_Р и температуры мокрого термометра t_М с помощью «i, d» – диаграммы.

Температура точки росы – это температура воздуха в насыщенном состоянии при данном влагосодержании. На «i, d» – диаграмме для определении t_Р необходимо из точки данного состояния воздуха (точка А на рис. ниже) опуститься по линии d = const до пересечения с линией насыщения φ = 100 % (точка Б). В таком случае изотерма, проходящая через точку Б, соответствует t_Р.

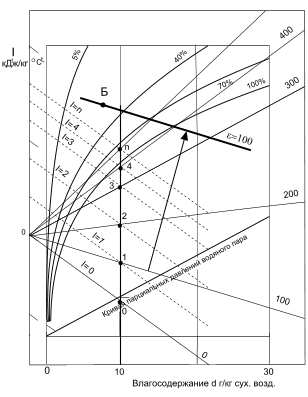
Рис. 7.6.

Построение на «i, d» – диаграмме углового масштаба.

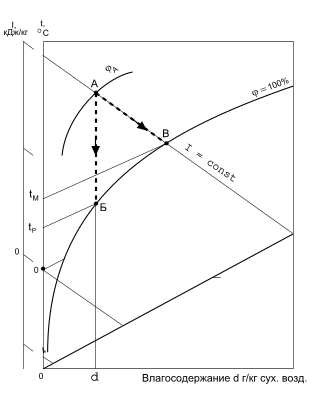
Рис. 7.7.

Определение значений t_Р и t_М на «i,d» – диаграмме

Температура мокрого термометра t_М равна температуре воздуха в насыщенном состоянии при данной энтальпии. В «i, d» – диаграмме t_М проходит через точку пересечения изотермы с линией φ = 100 % (точка В) и практически совпадает (при параметрах, имеющих место в системах кондиционирования) с линией I = const, проходящей через точку Б.

Изображение процессов нагревания и охлаждения воздуха на «i, d» -диаграмме. Процесс нагревания воздуха в поверхностном теплообменнике – калорифере в «i, d» – диаграмме изображается вертикальной линией АБ (см. рис.ниже) при d = const, так как влагосодержание воздуха при контакте с сухой нагретой поверхностью не изменяется. Температура и энтальпия при нагревании увеличивается, а относительная влажность уменьшается.

Процесс охлаждения воздуха в поверхностном теплообменнике-воздухоохладителе может быть реализован двумя путями. Первый путь – охлаждение воздуха при постоянном влагосодержании (процесс а на рис. 1.6). Этот процесс при d = const протекает в том случае, если температура поверхности воздухоохладителя будет выше температуры точки росы t_Р. Процесс пройдет по линии ВГ или в крайнем случае – по линии ВГ’.

Второй путь – охлаждение воздуха при уменьшении его влагосодержания, что возможно только при выпадении влаги из воздуха (случай б на рис. 7.8). Условие реализации такого процесса – температура поверхности воздухоохладителя или любой другой поверхности, контактирующей с воздухом должна быть ниже температуры точки росы воздуха в точке Д. В этом случае будет происходить конденсация водяного пара в воздухе и процесс охлаждения будет сопровождаться уменьшением влагосодержания в воздухе. На рис. этот процесс пойдет по линии СЖ, причем точка Ж соответствует температуре t_П.В. поверхности воздухоохладителя. На практике процесс охлаждения заканчивается раньше и достигает, например, точки Е при температуре t_Е.

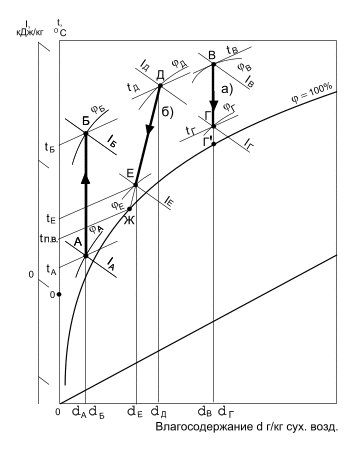
Рис. 7.8. Изображение процессов нагревания и охлаждения воздуха на «i, d» – диаграмме

Процессы смешения двух потоков воздуха в «i, d» – диаграмме.

В системах кондиционирования воздуха используются процессы смешения двух потоков воздуха с различным их состоянием. Например, использование рециркуляционного воздуха или смешение подготовленного воздуха с воздухом внутри помещения при подаче его из кондиционера. Возможны и другие случаи смешения.

Представляет интерес для расчетов процессов смешения найти связь между аналитическими расчетами процессов и их графическими изображениями на «i, d» – диаграмме. На рис. 7.9 представлены два случая осуществления процессов смешения: а) – точка состояния воздуха на «i, d» – диаграмме лежит выше линии φ = 100 % и случай б) – точка смеси лежит ниже линии φ = 100 %.

Рассмотрим случай а). Воздух состояния точки А в количестве G_А с параметрами d_А и i_А смешивается с воздухом состояния точки В в количестве G_B c параметрами d_B и i_B. При этом принимают условие, что расчеты производятся на 1 кг воздуха состояния А. Тогда величиной n = G_В/G_А оценивают, какое количество воздуха состояния точки В приходится на 1 кг воздуха состояния точки А. Для 1 кг воздуха состояния точки А можно записать балансы теплоты и влаги при смешении

i_A + i_B = (1 + n)i_СМ ;

d_A + nd_B = (1 + n)d_СМ ,

где i_СМ и d_СМ – параметры смеси.

Из уравнений получают:

.

Уравнение является уравнением прямой линии, любая точка которой указывает параметры смешения i_СМ и d_СМ. Положение точки смешения С на прямой АВ может быть найдено по соотношению сторон подобных треугольников АСД и СВЕ.

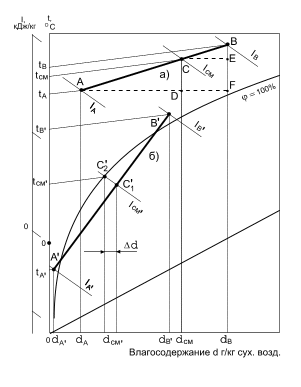
Рис. 7.9. Процессы смешения воздуха в «i, d» – диаграмме. а) – точка смеси лежит выше линии φ = 100 %; б) – точка смеси лежит ниже φ = 100 %.

,

т.е. точка С делит прямую АВ на части, обратно пропорциональные массам смешиваемого воздуха.

Если положение точки С на прямой АВ известно, то можно найти массы G_A и G_B. Из уравнения следует

,

тогда

.

Аналогично

.

На практике возможен случай, когда в холодный период года точка смеси С₁’ лежит ниже линии φ = 100 %. В этом случае в процессе смешения будет иметь место конденсация влаги. Сконденсированная влага выпадает из воздуха и будет находиться после смешения в состоянии насыщения при φ = 100 %. Параметры смеси достаточно точно определяются точкой пересечения линии φ = 100 % (точка С₂) и i_СМ = const. При этом количество выпавшей влаги равно Δd.