14. Механическая система. Силы внешние и внутренние.

 Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных.

Материальное абсолютно твердое тело мы также будем рассматривать как систему материальных точек, образующих это тело и связанных между собой так, что расстояния между ними не изменяются, все время остаются постоянными.

Классическим примером механической системы является солнечная система, в которой все тела связаны силами взаимного притяжения. Другим примером механической системы может служить любая машина или механизм, в которых все тела связаны шарнирами, стержнями, тросами, ремнями и т.п. (т.е. различными геометрическими связями). В этом случае на тела системы действуют силы взаимного давления или натяжения, передаваемые через связи.

Совокупность тел, между которыми нет никаких сил взаимодействия (например, группа летящих в воздухе самолетов), механическую систему не образует.

В соответствии со сказанным, силы, действующие на точки или тела системы, можно разделить на внешние и внутренние.

Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.

Внутренними называются силы, действующие на точки системы со стороны других точек или тел этой же системы. Будем обозначать внешние силы символом -  , а внутренние -  .

Как внешние, так и внутренние силы могут быть в свою очередь или активными, или реакциями связей.

Реакции связей или просто – реакции, это силы которые ограничивают движение точек системы (их координаты, скорость и др.). В статике это были силы заменяющие связи. В динамике для них вводится более общее определение.

Активными или задаваемыми силами называются все остальные силы, все кроме реакций.

Момент импульса  системы материальных  точек

 

Если тело представить как систему материальных точек (м.т.), то можно найти момент импульса тела относительно полюса 0.

Вектор момента импульса системы м.т. (тела) относительно полюса 0 равен геометрической сумме векторов моментов импульса, действующих на каждую м.т. в отдельности относительно того же полюса 0:

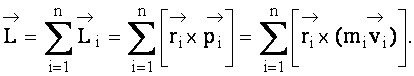
или

.

Переходя к модулю момента импульса тела относительно полюса 0 и используя связь линейной с угловой скоростью (v_i=r_i),  после подстановки в последнее выражение, получим:

L= I.

(5.13)

 Используя скамью Жуковского,  в видеоопыте "Векторное сложение моментов импульса" демонстрируется сохранение момента импульса в начале  вращательного движения, при изменении направления момента импульса, при изменении момента инерции.

Теорема об изменении кинетической энергии системы материальных точек.

Разделяя силы, действующие на точки системы, на внешние и внутренние, запишем для каждой точки системы теорему об изменении кинетической энергии в интегральной форме:

где A_i^e - работа внешних сил системы, приложенных к точке системы с номером i, а A_iⁱ - работа внутренних сил системы, приложенных к той же точке. Складывая между собой правые и левые части этих равенств, имеем

Сумму кинетических энергий всех точек системы обозначим T и назовем кинетической энергией системы, ту же сумму в начальном положении точек системы обозначим T₀ и назовем кинетической энергией системы в ее начальном положении, сумму работ внешних сил обозначим A^e и назовем работой внешних сил системы, сумму работ внутренних сил обозначим Aⁱ и назовем работой внутренних сил системы.

Подставляя введенные обозначения в последнее выражение, получим математическую запись теоремы об изменении кинетической энергии системы материальных точек в интегральной форме:

T - T0 = Ae + Ai

(22)

то есть: изменение кинетической энергии системы при ее переходе из начального положение в текущее (или конечное) положение равно работе внешних и внутренних сил системы, совершенной при этом переходе.

Дифференцируя (22) по времени, учитывая, что кинетическая энергия системы в начальном положении - величина постоянная, имеем dT / dt = dA^e / dt + dAⁱ / dt. Откуда, зная что производная от работы является мощностью, получаем

dT / dt = Ne + Ni

(23)

Уравнение (23) представляет собой математическую запись теоремы об изменении кинетической энергии системы материальных точек в дифференциальной форме: производная по времени от кинетической энергии системы равна мощности внутренних и внешних сил системы.

Как показывают формулы (22) и (23), в отличие от предыдущих общих теорем динамики, в теорему об изменении кинетической энергии системы входят внутренние силы. То есть непосредственно за счет внутренних сил нельзя изменить ни количество движения системы, ни ее момент количеств движения, но можно изменить ее кинетическую энергию.

При практическом применении теоремы необходимо уметь вычислять кинетическую энергию системы материальных точек и твердого тела.

закон изменения момента импульса.

 

Рассмотрим произвольную систему тел. Моментом импульса системы назовем величину L, равную векторной сумме моментов импульсов отдельных ее частей L_i, взятых относительно одной и той же точки выбранной системы отсчета.

                                            L = ΣL_i.                                                           

Найдем скорость изменения момента импульса системы. Проведя рассуждения, аналогичные описанию вращательного движения твердого тела, получим, что

скорость изменения момента импульса системы равна векторной сумме моментов внешних сил M, действующих на части этой системы.

                                     dL/dt = M.                                                      

Причем вектора L и M задаются относительно одной и той же точки O в выбранной СО. Уравнение (21) представляет собой закон изменения момента импульса системы.

Причиной изменения момента импульса является действующий на систему результирующий момент внешних сил. Изменение момента импульса за конечный промежуток времени можно найти, воспользовавшись выражением

                                      .                                           

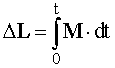Приращение момента импульса системы равно импульсу результирующего момента внешних сил, действующих на нее.

В неинерциальной системе к моменту внешних сил необходимо прибавить момент сил инерции относительно выбранной точки O.

Закон сохранения момента импульса. 

 

Из закона изменения момента импульса, полученного нами для системы тел, вытекает закон сохранения момента импульса применительно к механике:

момент импульса системы тел сохраняется неизменным при любых взаимодействиях внутри системы, если результирующий момент внешних сил, действующих на нее, равен нулю.

Еще раз подчеркнем, что при использовании этого закона моменты импульса и сил необходимо брать относительно одно и той же оси.

Закон сохранения момента импульса является фундаментальным законом природы и выполняется для любых, а не только механических систем.

Следствия из закон сохранения момента импульса:

        в случае изменения скорости вращения одной части системы другая также изменит скорость вращения, но в противоположную сторону таким образом, что момент импульса системы не изменится;

        если момент инерции замкнутой системы в процессе вращения изменяется, то изменяется и ее угловая скорость таким образом, что момент импульса системы останется тем же самым;

        в случае, когда сумма моментов внешних сил относительно некоторой оси равняется нулю, момент импульса системы относительно этой же оси остается постоянным.

Фундаментальные взаимодействия

Одним из величайших достижений физики за последние два тысячелетия стало выделение и определение четырех видов взаимодействия, которые правят Вселенной. Все они могут быть описаны на языке полей, которым мы обязаны Фарадею. К несчастью, однако, ни один из четырех видов не обладает в полной мере свойствами силовых полей, описанных в боль­шинстве фантастических произведений. Перечислим эти виды взаимодействия. 1. Гравитация. Безмолвная сила, не позволяющая нашим ногам оторваться от опоры. Она не дает рассыпаться Земле и звездам, помогает сохранить целостность Солнечной системы и Галактики. Без гравитации вращение планеты вышвырнуло бы нас с Земли в космос со скоростью 1000 миль в час. Проблема в том, что свойства гравитации в точности противоположны свойствам фантастических силовых полей. Гравитация — сила притяжения, а не отталкивания; она чрезвычайно слаба — относительно, разумеется; она работает на громадных, астрономических расстояниях. Другими словами, являет собой почти полную противоположность плоскому, тонкому, непроницаемому барьеру, который можно встретить едва ли не в любом фантастическом романе или фильме. К примеру, перышко к полу притягивает целая планета — Земля, но мы легко можем преодолеть притяжение Земли и поднять перышко одним пальцем. Воздействие одного нашего пальца способно преодолеть силу притяжения целой планеты, которая весит больше шести триллионов килограммов. 2. Электромагнетизм (ЭМ).  Сила, освещающая наши города. Лазеры, радио, телевидение, современная электроника, компьютеры, Интернет, электричество, магнетизм — все это следствия проявления электромагнитного взаимодействия. Возможно, это самая полезная сила, которую удалось обуздать человечеству на протяжении всей его истории. В отличие от гравитации она может работать и на притяжение, и на отталкивание. Однако и она не годится на роль силового поля по нескольким причинам. Во-первых, ее можно легко нейтрализовать. К примеру, пластик или любой другой непроводящий материал без труда проникнет в мощное электрическое или магнитное поле. Кусок пластика, брошенный в магнитное поле, свободно пролетит его насквозь. Во-вторых, электромагнетизм действует на больших расстояниях, его непросто сосредоточить в плоскости. Законы ЭМ-взаимодействия описываются уравнениями Джеймса Клерка Максвелла, и похоже, силовые поля не являются решением этих уравнений. 

3 и 4. Сильные и слабые ядерные взаимодействия.  Слабое взаимодействие — это сила радиоактивного распада, та, что разогревает радиоактивное ядро Земли. Эта сила стоит за извержениями вулканов, землетрясениями и дрейфом континентальных плит. Сильное взаимодействие не дает рассыпаться ядрам атомов; оно обеспечивает энергией солнце и звезды и отвечает за освещение Вселенной. Проблема в том, что ядерное взаимодействие работает только на очень маленьких расстояниях, в основном в пределах атомного ядра. Оно так прочно связано со свойствами самого ядра, что управлять им чрезвычайно трудно. В настоящее время нам известно только два способа влиять на это взаимодействие: мы можем разбить субатомную частицу на части в ускорителе или взорвать атомную бомбу. Хотя защитные поля в научной фантастике и не подчиняются известным законам физики, все же существуют лазейки, которые в будущем, вероятно, сделают создание силового поля возможным. Во-первых, существует, возможно, пятый вид фундаментального взаимодействия, который никому до сих пор не удалось увидеть в лаборатории. Может оказаться, к примеру, что это взаимодействие работает только на расстояниях от нескольких дюймов до фута — а не на астрономических расстоя­ниях. (Правда, первые попытки обнаружить пятый вид взаимо­действия дали отрицательные результаты.) Во-вторых, нам, возможно, удастся заставить плазму имитировать некоторые свойства силового поля. Плазма — это «четвертое состояние вещества». Три первые, привычные нам состояния вещества, — твердое, жидкое и газообразное; тем не менее самой распространенной формой вещества во вселенной является плазма: газ, состоящий из ионизированных атомов. Атомы в плазме не связаны между собой и лишены электронов, а потому обладают электрическим зарядом. Ими можно без труда управлять при помощи электрического и магнитного полей. Видимое вещество вселенной существует по большей части в форме различного рода плазмы; из нее образованы солнце, звезды и межзвездный газ. В обычной жизни мы почти не сталкиваемся с плазмой, потому что на Земле это явление редкое; тем не менее плазму можно увидеть. Для этого доста­точно взглянуть на молнию, солнце или экран плазменного телевизора.

15. Сила трения скольжения — силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.

Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения и не зависит от площади соприкосновения. (Это можно объяснить тем, что никакое тело не является абсолютно ровным. Поэтому истинная площадь соприкосновения гораздо меньше наблюдаемой. Кроме того, увеличивая площадь, мы уменьшаем удельное давление тел друг на друга.) Величина, характеризующая трущиеся поверхности, называется коэффициентом трения, и обозначается чаще всего латинской буквой «k» или греческой буквой «μ». Она зависит от природы и качества обработки трущихся поверхностей. Кроме того, коэффициент трения зависит от скорости. Впрочем, чаще всего эта зависимость выражена слабо, и если большая точность измерений не требуется, то «k» можно считать постоянным.

В первом приближении величина силы трения скольжения может быть рассчитана по формуле:

, где

 — коэффициент трения скольжения,

 — сила нормальной реакции опоры.

По физике взаимодействия трение принято разделять на:

• Сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазками — очень редко встречающийся на практике случай. Характерная отличительная черта сухого трения — наличие значительной силы трения покоя.

• Сухое с сухой смазкой (графитовым порошком)

• Жидкостное, при взаимодействии тел, разделённых слоем жидкости или газа (смазки) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость;

• Смешанное, когда область контакта содержит участки сухого и жидкостного трения;

• Граничное, когда в области контакта могут содержатся слои и участки различной природы (окисные плёнки, жидкость и т. д.) — наиболее распространённый случай при трении скольжения.

В связи со сложностью физико-химических процессов, протекающих в зоне фрикционного взаимодействия, процессы трения принципиально не поддаются описанию с помощью методов классической механики.

При механических процессах всегда происходит в большей или меньшей степени преобразование механического движения в другие формы движения материи (чаще всего в тепловую форму движения). В последнем случае взаимодействия между телами носят названия сил трения.

Опыты с движением различных соприкасающихся тел (твёрдых по твёрдым, твёрдых в жидкости или газе, жидких в газе и т. п.) с различным состоянием поверхностей соприкосновения показывают, что силы трения проявляются при относительном перемещении соприкасающихся тел и направлены против вектора относительной скорости тангенциально к поверхности соприкосновения. При этом всегда происходит нагревание взаимодействующих тел.

Силами трения называются тангенциальные взаимодействия между соприкасающимися телами, возникающие при их относительном перемещении. Силы трения возникающие при относительном перемещении различных тел, называются силами внешнего трения.

Силы трения возникают и при относительном перемещении частей одного и того же тела. Трение между слоями одного и того же тела называется внутренним трением.

В реальных движениях всегда возникают силы трения большей или меньшей величины. Поэтому при составлении уравнений движения, строго говоря, мы должны в число действующих на тело сил всегда вводить силу трения F тр.

Тело движется равномерно и прямолинейно, когда внешняя сила уравновешивает возникающую при движении силу трения.

Для измерения силы трения, действующей на тело, достаточно измерить силу, которую необходимо приложить к телу, чтобы оно двигалось без ускорения.

Тре́ние каче́ния — сопротивление движению, возникающее при перекатывании тел друг по другу. Проявляется, например, между элементами подшипников качения, между шинойколеса автомобиля и дорожным полотном. В большинстве случаев величина трения качения гораздо меньше величины трения скольжения при прочих равных условиях, и потому качение является распространенным видом движения в технике.

Трение качения возникает на границе двух тел, и поэтому оно классифицируется как вид внешнего трения.

Сила трения качения

Рис. 1.   — реакция опоры;   — прижимающая сила;   — сила трения качения,   — внешняя сила (приложена к центру тела и направлена вправо, на рисунке не показана); сумма векторов сил 

Пусть на тело вращения, располагающееся на опоре, действуют

P — внешняя сила, пытающаяся привести тело в состояние качения или поддерживающая качение и направленная вдоль опоры;

N — прижимающая сила;

 — реакция опоры.

Если векторная сумма этих сил равна нулю

то ось симметрии тела движется равномерно и прямолинейно или остаётся неподвижной (см. рис. 1). Вектор   определяет силу трения качения, противодействующую движению. Это означает, что прижимающая сила уравновешивается вертикальной составляющей реакции опоры, а внешняя сила уравновешивается касательной составляющей реакции опоры.

Рис. 2.   — внешняя сила;   — сила трения качения; R — радиус тела вращения; 

Равномерное качение означает также, что сумма моментов сил относительно произвольной точки равна нулю. Из равновесия относительно оси вращения моментов сил, изображённых на рис. 2 и 3, следует:

откуда

где

 — сила трения качения;

f — коэффициент трения качения, имеющий размерность длины (следует отметить важное отличие от коэффициента трения скольжения, который безразмерен);

R — радиус катящегося тела;

N — прижимающая сила.

Рис. 3. Момент силы трения   действующий против часовой стрелки (относительно мгновенного центра вращения в зоне контакта — правого конца отрезка f) и тормозящий качение тела вправо; N — прижимающая сила; f — коэффициент трения качения, равный длине плеча силы N.

Рис. 4. Коэффициент трения f;   — асимметричная реакция опорной поверхности, векторная сумма вертикальной   и горизонтальной   компонент;   — прижимающая сила;   — сила трения качения.

Эта зависимость подтверждается экспериментально. Для малой скорости качения сила трения качения не зависит от величины этой скорости. Когда скорость качения достигает значений, сопоставимых со значениями скорости деформации в материале опоры, трение качения резко возрастает и даже может превысить трение скольжения при аналогичных условиях.

[править]Момент сил трения качения

Определим для подвижного цилиндра момент, тормозящий вращательное движение тела. Рассматривая данный момент относительно оси вращающегося колеса (например, колеса автомобиля), находим, что он равен произведению тормозного усилия на оси на радиус колеса. Относительно точки контакта движущегося тела с землей момент будет равен произведению внешней силы, уравновешивающей силу трения, на радиус колеса (рис. 2):

.

С другой стороны, момент трения равен моменту прижимающей силы   на плечо, длина которого равна коэффициенту трения качения f:

где

 — момент силы трения в [Н] · [м];

R — радиус тела качения;

P — внешняя сила;

 — сила трения качения;

f — коэффициент трения качения в [м].

[править]Коэффициент трения качения

Из выписанного выше уравнения следует, что коэффициент трения качения может быть определен как отношение момента трения качения  к прижимной силе N:

Графическая интерпретация коэффициента трения качения f дана на рис. 3 и 4.

Коэффициент трения качения имеет следующие физические интерпретации:

Если тело находится в покое и внешняя сила отсутствует, то реакция опоры лежит на той же линии, что и прижимающая сила. Когда тело катится, то из условия равновесия следует, что нормальная составляющая реакции опоры параллельна и противонаправлена прижимающей силе, но не лежит с ней на одной линии. Коэффициент трения качения равен расстоянию между прямыми, вдоль которых действуют прижимающая сила и нормальная составляющая реакции опоры (рис. 4).

Движение катящегося тела без проскальзывания можно рассматривать как поворот вокруг мгновенной оси вращения (на рис. 4 — точка приложения вектора  ), которая для абсолютно твёрдых тел совпадает с основанием перпендикуляра, опущенного из центра круга на опору. Для случая реальных (деформирующихся под нагрузкой) материалов мгновенный центр вращения смещён в направлении качения тела, а величина смещения равна значению коэффициента трения качения.