Вид преобразований при коллинеарных осях[4]

Если ИСО S движется относительно ИСО S' с постоянной скоростью   вдоль оси  , а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид:

или, используя векторные обозначения,

(последняя формула остается верной для любого направления осей координат).

Как видим, это просто формулы для сдвига начала координат, линейно зависящего от времени (подразумеваемого одинаковым для всех систем отсчета).

Из этих преобразований следуют соотношения между скоростями движения точки и её ускорениями в обеих системах отсчета:

Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для малых скоростей   (много меньше скорости света).

[править]Формула преобразования скоростей

Достаточно продифференцировать   в формуле преобразований Галилея, приведенной выше, и сразу же получится приведенная в том же параграфе рядом формула преобразования скорости.

Приведем более элементарный, но и более общий вывод — для случая произвольного движения начала отсчета одной системы относительно другой (при отсутствии вращения). Для такого более общего случая, можно получить формулу преобразования скоростей, например, так.

Рассмотрим преобразование произвольного сдвига начала отсчета на вектор  ,

где радиус-вектор какого-то тела A в системе отсчета K обозначим за  , а в системе отсчета K' — за  ,

подразумевая, как всегда в классической механике, что время   в обеих системах отсчета одно и то же, а все радиус-векторы зависят от этого времени:  .

Тогда в любой момент времени

и в частности, учитывая

,

имеем:

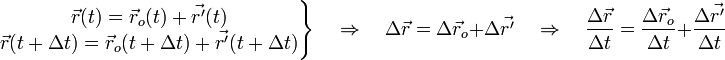
где:

 — средняя скорость тела A относительно системы K;

 — средняя скорость тела А относительно системы K' ;

 — средняя скорость системы K' относительно системы K.

Если   то средние скорости совпадают с мгновенными:

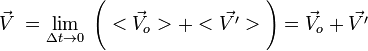
или короче

— как для средних, так и для мгновенных скоростей (формула сложения скоростей).

Таким образом, скорость тела относительно неподвижной системы координат равна векторной сумме скорости тела относительно движущейся системы координат и скорости системы отсчета относительно неподвижной системы отсчета. Аналогично можно получить формулу преобразования ускорений при переходе из одной системы координат в другую, верную при условии, что эти системы движутся поступательно друг относительно друга:

[править]Принцип относительности Галилея

Из формулы для ускорений следует, что если движущаяся система отсчета движется относительно первой без ускорения, то есть  , то ускорение   тела относительно обеих систем отсчета одинаково.

Поскольку в Ньютоновской динамике из кинематических величин именно ускорение играет роль (см.второй закон Ньютона), то, если довольно естественно предположить, что силы зависят лишь от относительного положения и скоростей физических тел (а не их положения относительно абстрактного начала отсчета), окажется, что все уравнения механики запишутся одинаково в любой инерциальной системе отсчета — иначе говоря, законы механики не зависят от того, в какой из инерциальных систем отсчета мы их исследуем, не зависят от выбора в качестве рабочей какой-либо конкретной из инерциальных систем отсчета. Также — поэтому — не зависит от такого выбора системы отсчета наблюдаемое движение тел (учитывая, конечно, начальные скорости). Это утверждение известно как принцип относительности Галилея, в отличие от Принципа относительности Эйнштейна

Иным образом этот принцип формулируется (следуя Галилею) так: если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым.

Требование (постулат) принципа относительности вместе с преобразованиями Галилея, представляющимися достаточно интуитивно очевидными, во многом следует форма и структура ньютоновской механики (и исторически также они оказали существенное влияние на ее формулировку). Говоря же несколько более формально, они накладывают на структуру механики ограничения, достаточно существенно влияющие на ее возможные формулировки, исторически весьма сильно способствовавшие ее оформлению.

12. Меры действия сил. Консервативная система. 1)Элементарный импульс силы. Элементарные работы силы. 2)Работа силы на конечном перемещении. 3)Работа силы упругости. 4)Консервативные системы. Потенциальная энергия.

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Работа силы. Мощность

Работа силы. МощностьРабота. По определению работой постоянной силы F, совершаемой при перемещении тела на величину s, называется величина   

где a - угол между векторами F и s. Если воспользоваться понятием скалярного произведения двух векторов, то выражение для работы можно записать в виде:  Работа измеряется в джоулях (Дж): [A] = Дж = Н·м. 

Мощность. Пусть сила F, действуя в течение промежутка времени Dt, совершает работу DA. Средняя мощность N определяется как отношение величины работы к промежутку времени, за который она была совершена: 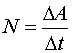 (14.2) Мощность измеряется в ваттах (Вт): [N] = Вт = Дж/с  Мо́щность — физическая величина, равная в общем случае скорости изменения энергии системы. В более узком смысле мощность равна отношениюработы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

Различают среднюю мощность за промежуток времени 

и мгновенную мощность в данный момент времени:

Интеграл от мгновенной мощности за промежуток времени равен полной переданной энергии за это время:

Векторное произведение радиуса-вектора   материальной точки на ее импульс:   называют моментом импульса  , этой точки относительно точки О Момент импульса   материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектораи импульса:

где   — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,   — импульс частицы.

Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:

где   — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.

(В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообще распределенной системы это может быть записано как   где   — импульс бесконечно малого точечного элемента системы).

В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.

Из определения момента импульса следует его аддитивность: как, для системы частиц в частности, так и для системы, состоящей из нескольких подсистем, выполняется:

.

• Замечание: в принципе момент импульса может быть вычислен относительно любого начала отсчета (получившиеся при этом разные значения связаны очевидным образом); однако чаще всего (для удобства и определенности) его вычисляют относительно центра масс или закрепленной точки вращения твердого тела итп).

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательногодвижения.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленнаядвижением.

13.