
- •Основные понятия.
- •Основные понятия.
- •Первый закон Ньютона (закон инерции Галилея -Ньютона).
- •Второй закон Ньютона.
- •Третий закон Ньютона.
- •§ 1.2. Способы задания движения точки
- •2. Криволинейное движение
- •6. Поступательное и вращательное движения абсолютно твердого тела
- •Первый закон Ньютона (закон инерции Галилея -Ньютона).
- •Второй закон Ньютона.
- •Третий закон Ньютона.
- •Вид преобразований при коллинеарных осях[4]
- •Теорема об изменении кинетической энергии материальной точки.
- •14. Механическая система. Силы внешние и внутренние.
- •Теорема об изменении кинетической энергии системы материальных точек.
- •Сила вязкого трения
- •16. Сила упругости
- •Виды деформации твердых тел Деформация растяжения
- •Деформация сжатия
- •Деформация сдвига
- •Деформация изгиба
- •Деформация кручения
- •Пластическая и упругая деформация
- •18. Работа и потенциальная энергия
- •Абсолютно неупругий удар
- •Динамика абсолютно твердого тела
- •§1 Момент инерции. Теорема Штейнера
- •27. Движение тела переменной массы
- •Механические колебания и волны
- •30. Графический метод сложения колебаний. Векторная диаграмма. Методом вращающегося вектора амплитуды.
- •Различные формы траектории суммы колебаний. Фигуры Лиссажу.
- •31. Сложение взаимно перпендикулярных колебаний.
- •Характеристики затухающих колебаний
- •33. Вынужденные механические колебания
- •Механическая волна
- •Основные характеристики волны
- •Уравнение бегущей волны
- •Продольная и поперечная волны
- •36. Энергетические характеристики волн
- •Энергия волны
- •Уравнение стоячей волны
- •Сущность явления
- •[Править]Математическое описание
- •[Править]Релятивистский эффект Доплера
- •Движение с постоянной скоростью
- •Строгое определение
- •[Править]Объяснение
- •Преобразования Лоренца в математике
- •[Править]Определение
- •[Править]Общие свойства
- •41. Относительность одновременности
- •[Править]Сокращение линейных размеров
- •[Править]Эффект Доплера
- •[Править]Аберрация
- •42. Релятивистская динамика [править]Энергия и импульс
- •[Править]Уравнения движения
- •[Править]Преобразования энергии и импульса
- •44. Дифференциальная форма
- •Уравнение неразрывности
- •45. Закон Бернулли
- •46. Вязкость. Ламинарные и турбулентные режимы течения
- •49. Основное уравнение мкт газа
- •[Править]Идеальные газы
- •Г.А.Белуха, школа № 4, г. Ливны, Орловская обл. Работа газа в термодинамике Методические рекомендации по изучению темы, 10-й класс
- •[Править]Определение
- •51. 3. Первое начало термодинамики
- •4.4 Теплоемкость
- •Физический смысл адиабатического процесса
- •[Править]Работа газа
- •Уравнение Пуассона для идеального газа [править]Адиабата Пуассона
- •[Править]Вывод уравнения
- •[Править]Показатель адиабаты
- •Политропный процесс
- •[Править]Показатель политропы
- •55. 3.9. Закон возрастания энтропии
- •Кпд тепловой машины Карно
- •Пра́вило фаз (или правило фаз Гиббса) — соотношение, связывающее число веществ (компонентов), фаз и степеней свободы в гетерогенной системе. Уравнение Гиббса
- •Условия фазового равновесия
- •[Править]Элементарный вывод
- •58. Капиллярные явления
2. Криволинейное движение
(движение материальной точки по окружности – простейшее криволинейное движение)
а) Равномерное движение материальной точки по окружности (модуль скорости t не изменяется, но направление скорости изменяется t 0 изменяется – рис. 18). Полное ускорение равно (12):
![]() ;
; ![]() ,т.е.
,т.е. ![]() .
.
б) Равнопеременное
движение материальной точки по
окружности (модуль
скорости изменяется, но |
|
= const ![]() t 0
и направление скорости изменяется – §
5). Полное ускорение равно (12):
t 0
и направление скорости изменяется – §
5). Полное ускорение равно (12):
![]() ;
; ![]() .
.
–
Если
направления векторов тангенциального
ускорения и скорости совпадают ![]() (модуль
скорости увеличивается: v > v0, но |
n|
= const u
n
0
и – рис. 16) – это
равноускоренное движение материальной
точки по окружности (
(модуль
скорости увеличивается: v > v0, но |
n|
= const u
n
0
и – рис. 16) – это
равноускоренное движение материальной
точки по окружности (![]() (
)
< 90°) – рис. 19.
(
)
< 90°) – рис. 19.
– Если направления векторов тангенциального ускорения и скорости противоположны: t (модуль скорости уменьшается: v < v0, но | | = const и n 0) – это равнозамедленное движение материальной точки по окружности ( ) > 90°) – рис. 19.
6. Поступательное и вращательное движения абсолютно твердого тела
1. Поступательным называется такое движение абсолютно твердого тела, при котором любая прямая, жестко связанная с телом, перемещается параллельно самой себе. Все точки тела, движущегося поступательно, в каждый момент времени имеют одинаковые скорости и ускорения, а их траектории полностью совмещаются при параллельном переносе. Поэтому кинематическое рассмотрение поступательного движения абсолютно твердого тела сводится к изучению движения любой его точки. В самом общем случае поступательно движущееся твердое тело обладает тремя степенями свободы. 2. Движение абсолютно твердого тела, при котором две его точки А и B остаются неподвижными, называется вращением (вращательным движением) вокруг неподвижной прямой АВ, называемой осью вращения. При вращении твердого тела вокруг неподвижной оси все его точки описывают окружности, центры которых лежат на оси вращения, а плоскости - перпендикулярны к ней. Тело, вращающееся вокруг неподвижной оси, обладает одной степенью свободы: его положение полностью определяется заданием угла f поворота из некоторого начального положения. 3. Угловой скоростью вращения твердого тела называется вектор w, численно равный первой производной от угла поворота по времени, w = df/dt и направленный вдоль оси вращения таким образом, чтобы из его конца вращение тела было видно происходящим против часовой стрелки. Направление вектора w совпадает с направлением поступательного движения буравчика, рукоятка которого вращается вместе с телом. 4. Линейная скорость v произвольной точки М вращающегося тела определяется как векторное произведение по формуле Эйлера v = [wr] где r - радиус-вектор, проведенный в точку М из произвольной точки О оси вращения тела. Численное значение v линейной скорости точки М прямо пропорционально ее расстоянию R от оси вращения: v = wr sina = wR где a - угол между векторами w и r. 5. Периодом обращения Т тела называется время, в течение которого тело поворачивается вокруг неподвижной оси вращения на угол f = 2p. 6. Угловым ускорением называется вектор e, равный первой производной от вектора угловой скорости по времени: e = dw/dt Угловое ускорение характеризует быстроту изменения во времени вектора угловой скорости тела. При вращении вокруг неподвижной оси направление вектора w сохраняется и e = dw/dt = d2f/dt2 причем вектор e совпадает но направлению с w в случае ускоренного вращения (e > 0) и противоположен ему по направлению в случае замедленного вращения (e < 0) Линейное ускорение произвольной точки М (r) вращающегося тела равно a = dv/dt = d/dt | wr | = | er | + | w | wr ||
Поступательное движение. Скорость. Ускорение. Простейшим видом механического движения абсолютно твердого тела является поступательное движение - такое движение, при котором тело перемещается параллельно самому себе. При поступательном движении твердого тела все его точки имеют одинаковые скорости и ускорения и описывают одинаковые траектории, смещенные относительно друг друга. Поступательное движение абсолютно твердого тела может быть охарактеризовано движением какой-либо одной его точки, например, центра масс. Для характеристики поступательного движения тела (материальной точка) вводится понятие перемещения.
Перемещением
называется вектор, соединяющий
начальное положение тела с его конечным
положением. Если положение точки в
декартовой системе координат задано
радиус-вектором, то перемещение можно
определить как разность
радиус-векторов
Δx, Δy, Δz – перемещение точки вдоль соответствующих осей.
В
общем случае перемещение не совпадает
с траекторией движения. Достаточно
малое перемещение, которое с определенной
степенью точности можно считать
совпадающим с соответствующим участком
траектории, называется элементарным
перемещением
Мгновенная
линейная скорость - физическая величина,
равная пределу отношения элементарного
перемещения
к
промежутку времени Δt, в течение
которого совершается это перемещение,
при
Мгновенная
скорость - векторная величина, имеющая
тоже направление, что и касательная
к траектории, т.к. вектор мгновенной
скорости
Средняя скалярная (путевая) скорость - физическая величина, определяемая отношением пути S, пройденного точкой за промежуток времени Δt к длительности этого промежутка:
Из (3) следует,
что
При
движении точки мгновенная скорость
может меняться как по величине, так и
по направлению. При этом
вектор Т.о., ускорение - векторная величина, характеризующая изменение скорости в единицу времени, численно равная первой производной от мгновенной скорости по времени или второй производной от перемещения по времени. В общем случае ускорение не совпадает по направлению с вектором скорости. Вектор ускорения а может быть представлен в виде 2-х взаимно перпендикулярных векторов: аn –нормальное ускорение, аt– тангенциальное ускорение. Вектор тангенциального ускорения аtнаправлен по касательной к траектории движения и определяет изменение модуля скорости. Вектор нормального ускорения направлен по нормали к траектории (т.е. к центру кривизны) и определяет изменение направления вектора скорости.
Как
видно из рисунка, полное
ускорение |
Вращательное движение и величины, его характеризующие Другим простейшим видом механического движения является вращательное движение абсолютно твердого тела. При таком движении его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат на одном прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Вращательное движение тела или точки характеризуется углом поворота, угловой скоростью и угловым ускорением. Угол поворота φ - это угол между двумя последовательными положениями радиуса вектора r, соединяющего тело или материальную точку с осью вращения. Угловое перемещение измеряется в радианах.
Угловая
скорость При равномерном вращении численное значение угловой скорости не меняется, т.е. ω = const.Равномерное вращение характеризуется:
- периодом вращения Т, т.е. временем, за которое тело делает один полный оборот, период обращения измеряется в с;
-
частотой
-
круговой (циклической,угловой)
частотой
Угловая
скорость может меняться как по величине,
так и по направлению. Векторная
величина, характеризующая изменение
угловой скорости в единицу времени и
численно равная второй производной
от углового перемещения по времени,
называется угловым ускорением: Если положение и радиус окружности, по которой происходит вращение не изменяется со временем, то направление векторов углового ускорения и угловой скорости совпадают, если вращение ускоренное, и противоположны, если вращение замедленное.
При
равномерном движении по окружности
тангенциальная составляющая ускорения
равна нулю, т.е. модуль линейной скорости
постоянен и определяется соотношением |
Связь между линейными и угловыми величинами, характеризующими движение
Отдельные
точки вращающегося тела имеют различные
линейные скорости v,
которые непрерывно изменяют свое
направление и зависят от угловой
скорости ω и расстояния r соответствующей
точки до оси вращения. Точка,
находящаяся на расстоянии r от оси
вращения проходит путь ΔS = rΔφ.
Поделим обе части равенства на Δt :
Таким
образом, чем дальше отстоит точка от
оси вращения, тем больше ее линейная
скорость. По определению ускорения,
Для Из (12) – (14) видно, что значения линейной скорости, тангенциального и нормального ускорений растут по мере удаления от оси вращения. Формула (12) устанавливает связь между модулями векторов v, r, ω, которые перпендикулярны друг к другу. |
7.
Сложное
движение точки (тела) –
такое движение, при котором точка (тело)
одновременно участвует в нескольких
движениях (напр. пассажир, перемещающийся
по движущемуся вагону). В этом случае
вводится подвижная система координат
(Oxyz),
которая совершает заданное движение
относительно неподвижной (основной)
системы координат (O1x1y1z1). Абсолютным
движением точки
назыв. движение по отношению к неподвижной
системе координат.Относительное
движение –
движение по отношению к подвижной
системе коорд. (движение по вагону). Переносное
движение –
движение подвижной сист. координат
относительно неподвижной (движение
вагона). Теорема
о сложении скоростей: ![]() ,
, 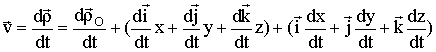 ;
; ![]() -орты
(единичные вектора) подвижной системы
координат, орт вращается вокруг мгновенной
оси, поэтому скорость его конца
-орты
(единичные вектора) подвижной системы
координат, орт вращается вокруг мгновенной
оси, поэтому скорость его конца 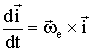 и
т.д., :
и
т.д., : ![]() ,
,
![]() ;
; ![]() –
относительная скорость.
–
относительная скорость.
![]() ;
переносная скорость:
;
переносная скорость: ![]() ,
поэтому абсолютная скорость точки =
геометрической сумме ее переносной
(ve)
и относительной (vr)
скоростей
,
поэтому абсолютная скорость точки =
геометрической сумме ее переносной
(ve)
и относительной (vr)
скоростей ![]() ,
модуль:
,
модуль: ![]() . Теорема
о сложении ускорений (теорема Кориолиса):
. Теорема
о сложении ускорений (теорема Кориолиса): 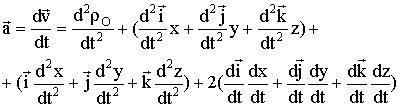
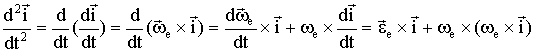 и
т.д. Слагаемые выражения, определяющего
ускорения
и
т.д. Слагаемые выражения, определяющего
ускорения ![]() :
1)
:
1) 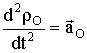 –
ускорение полюса О;
–
ускорение полюса О;
2) 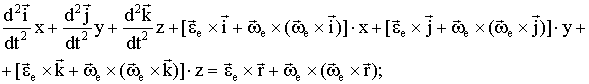
3) 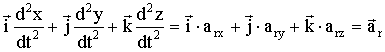 –
относительное ускорение точки;
–
относительное ускорение точки;
4) 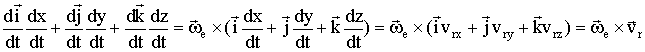 ,
,
получаем: ![]() .
.
Первые
три слагаемых представляют собой
ускорение точки в переносном движении:
![]() –
ускорение полюса О;
–
ускорение полюса О; ![]() –
вращательное уск.,
–
вращательное уск., ![]() –
осестремительное уск., т.е.
–
осестремительное уск., т.е. ![]() . Теорема
о сложении ускорений (теорема Кориолиса):
. Теорема
о сложении ускорений (теорема Кориолиса): ![]() ,
где
,
где ![]() –
ускорение Кориолиса (кориолисово
ускорение) – в случае непоступательного
переносного движения абсолютное
ускорение = геометрической сумме
переносного, относительного и кориолисова
ускорений. Кориолисово ускорение
характеризует: 1) изменение модуля и
направления переносной скорости точки
из-за ее относительного движения; 2)
изменение направления относительной
скорости точки из-за вращательного
переносного движения. Модуль ускорения
Кориолиса: ас=
2|evr|sin(e^vr),
направление вектора
–
ускорение Кориолиса (кориолисово
ускорение) – в случае непоступательного
переносного движения абсолютное
ускорение = геометрической сумме
переносного, относительного и кориолисова
ускорений. Кориолисово ускорение
характеризует: 1) изменение модуля и
направления переносной скорости точки
из-за ее относительного движения; 2)
изменение направления относительной
скорости точки из-за вращательного
переносного движения. Модуль ускорения
Кориолиса: ас=
2|evr|sin(e^vr),
направление вектора ![]() определяется
по правилу векторного произведения,
или по правилу Жуковского: проекцию
относительной скорости на плоскость,
перпендикулярную переносной угловой
скорости, надо повернуть на 90о в
направлении вращения.
определяется
по правилу векторного произведения,
или по правилу Жуковского: проекцию
относительной скорости на плоскость,
перпендикулярную переносной угловой
скорости, надо повернуть на 90о в
направлении вращения.
Кориолисово уск. = 0 в трех случаях: 1) e=0, т.е. в случае поступательного переносного движения или в момент обращения угл. скорости в 0; 2) vr=0; 3) sin(e^vr)=0, т.е. (e^vr)=0, когда относительная скорость vr параллельна оси переносного вращения. В случае движения в одной плоскости – угол между vr и вектором e = 90о, sin90o=1, ас=2evr.
Сложное движение твердого тела
При сложении двух поступательных движений результирующее движение также является поступательным и скорость результирующего движения равна сумме скоростей составляющих движений. Сложение вращений тв. тела вокруг пересекающихся осей. Ось вращения, положение которой в пространстве изменяется со временем назыв. мгновенной осью вращения тела. Вектор угловой скорости – скользящий вектор, направленный вдоль мгновенной оси вращения. Абсолютная угловая скорость тела = геометрической сумме скоростей составляющих вращений – правило параллелограмма угловых скоростей.
![]() .
Если тело участвует одновременно в
мгновенных вращениях вокруг нескольких
осей, пересекающихся в одной точке, то
.
Если тело участвует одновременно в
мгновенных вращениях вокруг нескольких
осей, пересекающихся в одной точке, то
![]() .
При сферическом движении твердого тела,
одна из точек которого во все время
движения остается неподвижной, имеем
уравнения сферического
движения: =f1(t); =f2(t); =f3(t). –
угол прецессии, – угол нутации, –
угол собственного вращения — углы
Эйлера. Угловая скорость прецессии
.
При сферическом движении твердого тела,
одна из точек которого во все время
движения остается неподвижной, имеем
уравнения сферического
движения: =f1(t); =f2(t); =f3(t). –
угол прецессии, – угол нутации, –
угол собственного вращения — углы
Эйлера. Угловая скорость прецессии ![]() ,
угл. скорость нутации
,
угл. скорость нутации ![]() ,
угл. ск. собственного вращения
,
угл. ск. собственного вращения ![]() .
. ![]() ,
,
![]() –
модуль
угловой скорости тела вокруг мгновенной
оси. Через проекции на неподвижные оси
координат:
–
модуль
угловой скорости тела вокруг мгновенной
оси. Через проекции на неподвижные оси
координат: ![]() –
кинематические уравнения Эйлера. Сложение
вращений вокруг 2-х параллельных осей.
–
кинематические уравнения Эйлера. Сложение
вращений вокруг 2-х параллельных осей.
1) Вращения
направлены в одну сторону. =2+1,
С – мгновенный центр скоростей и через
нее проходит мгновенная ось вращения, ![]() ,
, ![]() .
2) Вращения направлены в разные
стороны.
.
2) Вращения направлены в разные
стороны. ![]() , =2—1
, =2—1
С
– мгн. центр ск. и мгн. ось вращения,
.
Векторы угловых скоростей при вращении
вокруг ||-ых осей складываются так же,
как векторы параллельных сил. 3) Пара
вращений –
вращения вокруг ||-ных осей направлены
в разные стороны и угловые скорости по
модулю равны (![]() –
пара угловых скоростей). В этом
случае vA=vB,
результирующее движение тела –
поступательное ( или мгновенное
поступательное) движение со
скоростью v=1AB –
момент пары угловых скоростей
(поступательное движение педали
велосипеда относит-но рамы). Мгн. центр
скоростей находится в бесконечности. Сложение
поступательного и вращательного
движений.
1) Скорость поступательного движения к
оси вращения – плоскопараллельное
движение – мгновенное вращение вокруг
оси Рр с угловой скоростью ='.
–
пара угловых скоростей). В этом
случае vA=vB,
результирующее движение тела –
поступательное ( или мгновенное
поступательное) движение со
скоростью v=1AB –
момент пары угловых скоростей
(поступательное движение педали
велосипеда относит-но рамы). Мгн. центр
скоростей находится в бесконечности. Сложение
поступательного и вращательного
движений.
1) Скорость поступательного движения к
оси вращения – плоскопараллельное
движение – мгновенное вращение вокруг
оси Рр с угловой скоростью ='.
2) Винтовое
движение –
движение тела слагается из вращательного
движения вокруг оси Аа с угл.ск. и
поступательного со скоростью v||Аа.
Ось Аа – ось винта. Если v и в
одну сторону, то винт – правый, если в
разные – левый. Расстояние, проходимое
за время одного оборота любой точкой
тела, лежащей на оси винта, наз. шагом
винта – h.
Если v и постоянны,
то h=![]() =const,
при постоянном шаге любая ()М, не лежащая
на оси винта описывает винтовую
линию.
=const,
при постоянном шаге любая ()М, не лежащая
на оси винта описывает винтовую
линию. ![]() направлена
по касательной к винтовой линии.
направлена
по касательной к винтовой линии.
3) Скорость поступательного движения образует произвольный угол с осью вращения, в этом случае движение можно рассматривать как слагающееся из серии мгновенных винтовых движений, вокруг непрерывно изменяющихся винтовых осей – мгновенно–винтовое движение.
8. Основная задача динамики.
Если кинематика изучает движение геометрического объекта (т.е. не обладающего никакими свойствами материального тела, кроме свойства занимать определенное место в пространстве и изменять это положение с течением времени), то Динамика изучает движение реальных тел под действием приложенных к ним сил, т.е. под действием других тел. Установленные Ньютоном три закона механики лежат в основе динамики. Непосредственно их можно применять к простейшему случаю движения, когда движущееся тело рассматривается как материальная точка, т.е. когда размер и форма тела не учитывается и когда движение тела рассматривается как движение точки, обладающей массой. Для описания движения точки можно выбрать любую систему координат, относительно которой определяются характеризующие это движение величины. За тело отсчета может быть принято любое тело, движущееся относительно других тел. В динамике имеют дело с инерциальными системами координат, характеризуемыми тем, что относительно них свободная материальная точка движется с постоянной скоростью.
Прямая задача состоит в определении сил, действующих сил на точку
по известному закону движения и заданной ее массе. Данная задача решается
путем двукратного дифференцирования заданных уравнений движения с
последующим их умножением на массу, т.е. найденные проекции сил
позволяют определить модуль и направление вектора равнодействующих
сил.
Для свободной материальной точки в координатной форме
сформулировать первую задачу можно так.
Пусть задано движение материальной точки массой координатным
способом:
Используя дифференциальное уравнение (1.2), находим проекции сил:
Обратная задача. Состоит в определении закона движения точки по
заданной ее массе, действующей силе и известным начальным условиям.
Решение второй задачи динамики сводится к интегрированию
дифференциальных уравнений движения точки, например, в координатной
форме. Эта задача решается, как правило, значительно сложнее, так как
требует операции двукратного интегрирования уравнений движения точки с
последующим использованием начальных условий задачи. За начальные условия принимают время 0
0 = t и соответствующие ему
значения координат точки и проекций ее скоростей. Задача построения
решения системы дифференциальных уравнений движения материальной
точки, удовлетворяющей определенным начальным условиям, называется
задачей Коши. Однако эта задача может быть решена в замкнутой форме не
всегда. Чаще всего аналитическое решение конкретных задач
сопровождается существенными затруднениями, т.е. решение оказывается
громоздким или вовсе неосуществимым.
Для этого обращаются к численным методам решения
дифференциальных уравнений, например, методу конечных разностей (метод 12
сеток) или начальных параметров. В приложении приведена программа для
решения системы из n дифференциальных уравнений второго порядка с
использованием стандартной процедуры Рунге- Кутта.
9. Инертность - это свойство, присущее всем телам. Состоит оно в том, что для изменения скорости тела на заданную величину нужно, чтобы действие на него определенного другого тела длилось некоторое время. Чем это время больше, тем инертнее тело. Из двух взаимодействующих тел то тело более инертно, которое медленнее набирает скорость. Инертность, - это способность тела сохранять своё положение покоя или величину скорости в случае его столкновения с другим телом. Чем больше инертность, тем более тело сопротивляется другим телам в случае его столкновения с ними. Для каждой единицы тела есть своя инертность. Можно её обозначать в граммах.
Масса тела, это величина характеризующая её инертность.
Инертность — свойство тела в большей или меньшей степени препятствовать изменению своей скорости относительно инерциальной системы отсчёта при воздействии на него внешних сил. Мерой инертности в физике выступает инертная масса.
Ма́сса (от греч. μάζα) — скалярная физическая величина, одна из важнейших величин в физике. В современной физике понятие «количество вещества» имеет другой смысл, а концепцию «массы» можно трактовать несколькими способами:
Пассивная гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями — фактически эта масса положена в основу измерения массы взвешиванием в современной метрологии.
Активная гравитационная масса показывает, какое гравитационное поле создаёт само это тело — гравитационные массы фигурируют взаконе всемирного тяготения.
Инертная масса характеризует инертность тел и фигурирует в одной из формулировок второго закона Ньютона. Если произвольная сила винерциальной системе отсчёта одинаково ускоряет разные исходно неподвижные тела, этим телам приписывают одинаковую инертную массу.
И́мпульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:
 .
.Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная кмассивному телу сила является причиной изменения его скорости или возникновения в нём деформаций.[1]
Сила как векторная величина характеризуется модулем, направлением и «точкой» приложения силы. Последним параметром понятие о силе, как векторе в физике, отличается от понятия о векторе в векторной алгебре, где равные по модулю и направлению векторы, независимо от точки их приложения, считаются одним и тем же вектором . В физике эти векторы называются свободными векторами. В механике чрезвычайно распространено представление освязанных векторах, начало которых закреплено в определённой точке пространства или же может находиться на линии, продолжающей направление вектора (скользящие векторы)
10.

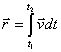 .
Величину пройденного точкой пути
можно представить графически площадью
фигуры ограниченной кривой v=f(t),прямыми t
= t1 и t
= t2 и
осью времени на графике скорости.
.
Величину пройденного точкой пути
можно представить графически площадью
фигуры ограниченной кривой v=f(t),прямыми t
= t1 и t
= t2 и
осью времени на графике скорости.