[Править]Элементарный вывод

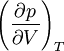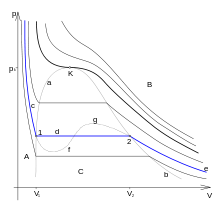
Между температурой фазового перехода и внешним давлением существует функциональная связь, причём при фазовом переходе производная   терпит разрыв. Тогда изотермы для рассматриваемого вещества будут иметь характерный вид, изображённый на рисунке. Для вывода существенен горизонтальный участок изотермы, соответствующий фазовому переходу. Слева и справа от этого участка всё вещество находится в одной фазе. Осуществим цикл Карно при бесконечно малой разности температур следующим образом: сначала сообщаем телу теплоту, переводя его из состояния 1 в состояние 2, затем адиабатически охлаждаем его на температуру dT, после чего замыкаем цикл, отводя теплоту и переводя вещество в фазу 1 с последующим адиабатическим нагревом. Совершённая работа равна площади цикла:

Сообщённая теплота равна

где   — удельная теплота фазового перехода,   — масса тела. Согласно теореме Карно,

Отсюда

57. полностью в папке

58. Капиллярные явления

Искривление поверхности жидкости у краев сосуда особенно отчетливо видно в узких трубках, где искривляется вся свободная поверхность жидкости. В трубках с узким сечением эта поверхность представляет собой часть сферы, ее называют мениском. У смачивающей жидкости образуется вогнутый мениск (рис. 1, а), а у несмачивающей — выпуклый (рис. 1, б). Так как площадь поверхности мениска больше, чем площадь поперечного сечения трубки, то под действием молекулярных сил искривленная поверхность жидкости стремится выпрямиться.

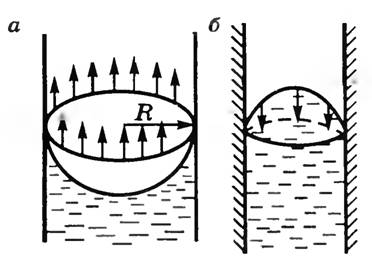
Рис. 1

Силы поверхностного натяжения создают дополнительное (лапласово) давление под искривленной поверхностью жидкости.

Для расчета избыточного давления предположим, что поверхность жидкости имеет форму сферы радиуса R (рис. 2. а), от которой мысленно отсечен шаровой сегмент, опирающийся на окружность радиуса r = R sin α.

Рис. 2

На каждый бесконечно малый элемент длины Δl этого контура действует касательная к поверхности сферы сила поверхностного натяжения, модуль которой  ΔF=αΔl. Разложим вектор  ΔF→ на две составляющие силы  ΔF→1 и  ΔF→2. Из рисунка 2, а видим, что геометрическая сумма сил  ΔF→2 для двух выделенных диаметрально противоположных элементов Δlравна нулю. Поэтому сила поверхностного натяжения направлена перпендикулярно плоскости сечения внутрь жидкости (рис. 2, в) и модуль ее равен

 F=∑ΔF1=∑ΔFsinα=∑αΔlrR=αrR∑Δl=αrR⋅2πr=2απr2R.

Избыточное давление, создаваемое этой силой

 p=FS

, где S = πr² — площадь основания сферического сегмента. Поэтому

 p=2απr2R⋅πr2=2αR.

Если поверхность жидкости вогнутая, то сила поверхностного натяжения направлена из жидкости (рис. 2, б) и давление под вогнутой поверхностью жидкости меньше, чем под плоской, на ту же величину  p=2αR . Эта формула определяет лапласово давление для случая сферической формы свободной поверхности жидкости. Она является частным случаем формулы Лапласа, определяющей избыточное давление для произвольной поверхности жидкости двоякой кривизны:

 p=α(1R1+1R2),

где R₁ и R₂ — радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности жидкости. Радиус кривизны положителен, если центр кривизны соответствующего сечения находится внутри жидкости, и отрицателен, если центр кривизны находится вне жидкости. Для цилиндрической поверхности (R₁ = l; R₂ = ∞) избыточное давление p=αR .

Если поместить узкую трубку (капилляр) одним концом в жидкость, налитую в широкий сосуд, то вследствие наличия силы лапласова давления жидкость в капилляре поднимается (если жидкость смачивающая) или опускается (если жидкость несмачивающая) (рис. 3, а, б), так как под плоской поверхностью жидкости в широком сосуде избыточного давления нет.

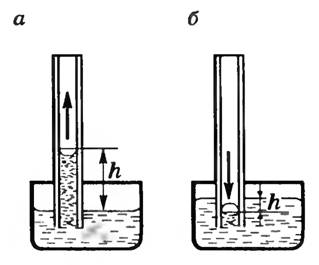
Рис. 3

Явления изменения высоты уровня жидкости в капиллярах по сравнению с уровнем жидкости в широких сосудах называются капиллярными явлениями.

Жидкость в капилляре поднимается или опускается на такую высоту h, при которой сила гидростатического давления столба жидкости уравновешивается силой избыточного давления, т.е.

 2αR=ρgh.

Откуда  h=2αρgR. Если смачивание не полное θ ≠ 0 (θ ≠ 180°), то, как показывают расчеты,  h=2αρgRcosθ.

Капиллярные явления весьма распространены. Поднятие воды в почве, система кровеносных сосудов в легких, корневая система у растений, фитиль и промокательная бумага — капиллярные системы.