Кпд тепловой машины Карно

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

.

Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику

.

Отсюда коэффициент полезного действия тепловой машины Карно равен

.

Из последнего выражения видно, что КПД тепловой машины Карно зависит только от температур нагревателя и холодильника. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равнаабсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.

Поэтому максимальный КПД любой тепловой машины будет меньше или равен КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Например, КПД идеального цикла Стирлинга равен КПД цикла Карно.

56. пдф

Пра́вило фаз (или правило фаз Гиббса) — соотношение, связывающее число веществ (компонентов), фаз и степеней свободы в гетерогенной системе. Уравнение Гиббса

Правило фаз записывается следующим образом:

где j — число фаз (например, агрегатных состояний вещества);

v — число степеней свободы, то есть независимых параметров (температура, давление, концентрация компонентов), которые полностью определяют состояние системы при равновесии и которые можно менять без изменения числа и природы фаз;

k — число компонентов системы — число входящих в систему индивидуальных веществ за вычетом числа химических уравнений, связывающих эти вещества. Иначе говоря, это минимальное количество веществ, из которых можно приготовить каждую фазу системы.

n — число переменных, характеризующих влияние внешних условий на равновесие системы.

При переменных давлении и температуре правило фаз сводится к выражению:

В случае однокомпонентной системы оно упрощается до:

,

Отсюда видно, например, что в однокомпонентной системе три фазы (j=3) могут сосуществовать при числе степеней свободы v, равном нулю, то есть при фиксированных давлении и температуре, что соответствует тройной точке на фазовой диаграмме. Две фазы (j=2) сосуществуют при произвольном измененнии либо давления, либо температуры, когда вторая из этих переменных не является независимой (v=1), то есть двухфазному равновесию на фазовой диаграмме соответствует линия. Если фаза одна (j=1), число степеней свободы системы равно двум, то есть температура и давление могут менятся независимо в пределах некоторой области на фазовой диаграмме — пока система не окажется на одной из линий двухфазного равновесия.

Иногда правило фаз записывают следующим образом:

то есть при равновесии число фаз в системе меньше либо равно числу компонентов плюс 2.

Условия фазового равновесия

В наиболее общей форме условия фазового равновесия можно получить, исходя из первого и второго начал термодинамики. Второе начало термодинамики в формулировке Клаузиуса дает ключ для получения условий равновесия: при равновесии энтропия изолированной системы максимальна. Это означает, что все самопроизвольные процессы, протекающие в изолированной системе, сопровождаются увеличением энтропии. Например, диффузия атомов и химические реакции ведут к увеличению энтропии.

Рассмотрим вопрос о том, какое из возможных состояний системы отвечает термодинамическому равновесию, т. е. при отсутствии внешнего воздействия может существовать неограниченно долго. Для равновесия недостаточно, чтобы какой-либо термодинамический потенциал имел экстремальное значение. Принцип экстремальности применим только в том случае, когда сравниваемые состояния удовлетворяют определенным условиям: например, рассматриваются состояния изолированной системы или состояния с постоянной температурой и давлением.

В изолированной системе при равновесии экстремального значения достигает энтропия. Однако гораздо чаще процессы протекают не в изолированной системе, а при постоянной температуре. Рассмотрим условие изотермического равновесия. Для таких систем справедливо основное неравенство термодинамики для неравновесных процессов

.

(13.8)

Если рассматривать изотермические процессы, протекающие при постоянном объеме, и перейти к независимым переменным, объему и температуре (V и T), то уравнение (13.8) примет вид

;  .

(13.9)

Следовательно, в рассматриваемой системе с неизменным количеством вещества могут протекать лишь такие процессы, при которых свободная энергия Гельмгольца не растет. Они прекращаются, как только свободная энергия F достигает минимума, что соответствует термодинамическому равновесию системы. Таким образом, при постоянных температуре (T) и объеме (V) состоянию равновесия отвечает минимум свободной энергии Гельмгольца  . Аналогично для энергии Гиббса (от p и T)

;  .

(13.10)

В этом случае равновесному состоянию системы отвечает минимум термодинамического потенциала Гиббса  .

Найденные условия термодинамического равновесия позволяют выделить равновесное состояние среди других, но они ничего не говорят о возможных внутренних условиях, определяющих равновесие между компонентами системы.

Исследуем условия равновесия фаз, имеющих в общем случае различный химический состав. Зафиксируем опять температуру (T) и давление (p). Тогда для системы из двух фаз α и β должно выполняться требование минимума термодинамического потенциала. В состоянии равновесия имеем

.

(13.11)

Поскольку температура, давление и общее количество вещества неизменны, то изменения возможны только в отношении состава фаз, т. е. какое-то количество компонента K может перейти из одной фазы в другую. При этом число молей компонента K в фазах α и β:  ,   изменяется на величины   и  . Тогда  . В результате

.

(13.12)

Это условие должно выполняться для любого изменения количества вещества  , для каждого компонента K, т. е.

.

(13.13)

Итак, при равновесии двух фаз химические потенциалы имеют одинаковую величину для каждого из компонентов, входящих в состав обеих фаз.

Рассмотрим равновесное состояние в многокомпонентной многофазной системе. Пусть фазы α и β находятся в равновесии друг с другом. В зависимости от природы межфазной границы возможны различные виды взаимодействия.

Механическое взаимодействие. Условием равновесия в этом случае служит равенство давлений в фазах ( ). Если поверхность не плоская, то давления могут отличаться за счет сил поверхностного натяжения.

Тепловое взаимодействие. Условием равновесия при тепловом взаимодействии является равенство температур фаз ( ).

Материальное взаимодействие. Этот вид взаимодействия обусловлен обменом частицами между фазами. В этом случае термодинамическое равновесие определяется равенством химических потенциалов фаз α и β ( ).

Таким образом, если система, состоящая из r фаз и n компонентов, находится в физико-химическом взаимодействии, то в равновесном состоянии для каждой из r фаз выполняются условия равенства давлений, температур и химических потенциалов:

.

(13.14)

В общем случае число уравнений в системе (13.14) меньше числа переменных, так что некоторые из переменных и в случае равновесия могут изменяться произвольно. Число таких переменных называется числом степеней свободы системы.

Подсчитаем число степеней свободы f равновесного состояния системы, состоящей из n компонентов, в различных фазах, число которых r. Для полного описания системы необходимо задать концентрации компонентов в r-фазах, температуру и давление. Для каждой K-й фазы получаем   независимых концентраций, а для всех r-фаз число независимых концентраций будет  . Задавая, кроме того, давление p и температуру T, получим полное число переменных  . Из этого числа нужно вычесть число уравнений связи (13.14). Каждая строка системы уравнений (13.14) содержит   независимых уравнений, а вся система уравнений − соответственно   независимых уравнений. В результате получим соотношение

; ,

(13.15)

где f − число степеней свободы. Т. е. количество степеней свободы термодинамической системы равно разности числа компонентов этой системы и числа фаз плюс две степени свободы за счет температуры и давления. Уравнение (13.15) носит название правило фаз Гиббса.

Поскольку число степеней свободы  , то  . Таким образом, в системе, находящейся в равновесии, число фаз не может превышать  , где n – число компонентов системы.

В случае однокомпонентной системы она может содержать одну, две или три фазы. Например, это могут быть жидкая, твердая и газообразная фазы. При трехфазном равновесии число степеней свободы  , т. е. такое равновесие возможно только при определенных значениях давления (p) и температуры (T).

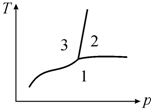
На фазовой диаграмме состояние трехфазного равновесия изображается тройной точкой (рис. 13.2).

 

Рис. 13.2. Кривые фазового равновесия в однокомпонентной системе (точка пересечения кривых − тройная точка)

 

При двухфазном равновесии имеется одна термодинамическая степень свободы  . Это означает, что одна из величин p или T может меняться произвольно, а другая будет определяться уравнением

,

(13.16)

где   и   – химические потенциалы рассматриваемых фаз. Связь между давлением и температурой в графическом представлении  это линии двухфазного равновесия, изображенные на рис. 13.2 в виде трех соединяющихся в одной точке линий.

Для однофазного равновесия   и значения давления p и температуры T могут меняться в пределах определенных областей (на рис. 13.2 − области 1, 2, 3), в каждой из которых существует соответственно твердая, жидкая и газообразная фазы.

В случае равновесия в системах, представляющих собой металлические сплавы, можно ограничиться конденсированными состояниями (т. е. твердым и жидким). Тогда число степеней свободы уменьшается на единицу

.

(13.17)

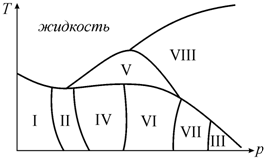
Этот подход правомерен, если давлением можно пренебречь (например, в случае, когда давление паров металлов мало). Однако некоторые системы очень чувствительны к изменению давления. Например, для висмута давление оказывает такую роль, что на фазовой диаграмме имеется целых 8 областей, соответствующих различным кристаллическим модификациям (рис. 13.3).

 

Рис. 13.3. Схематическая (p−T)-диаграмма состояний висмута [55]

 

Условия фазового равновесия, как показано на рис. 13.3, можно описывать не только аналитически, но и графически. Для графического описания используют диаграммы фазовых равновесий, или фазовые диаграммы. Фазовая диаграмма многокомпонентной системы ( ) − геометрическое изображение фазовых состояний (равновесий и превращения фаз), которые реализуются при тех или иных параметрах в результате взаимодействия компонентов, входящих в систему.

Диаграммы фазового равновесия многокомпонентных систем строят в координатах p − T − X ), где X − концентрация компонентов, а однокомпонентных систем − в координатах p − T. Каждая точка диаграммы фазового равновесия характеризует параметры физико-химических систем, образующихся в результате взаимодействия компонентов, для которых построена диаграмма фазового равновесия.

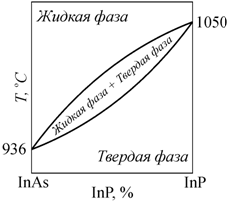
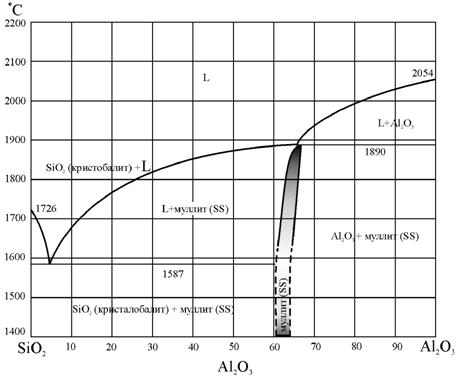
Диаграммы фазового равновесия в координатах концентрация−температура (диаграммы T−X) для двухкомпонентных систем изображаются на плоскости. Простейший пример такой диаграммы для полупроводникового соединения, где компонентами являются индий, мышьяк и фосфор (InAs − InP), показан на рис. 13.4. Такой вид фазовой диаграммы характерен для  твердых растворов с неограниченной растворимостью. Более сложный вид имеют фазовые диаграммы в системах с ограниченной растворимостью. Подобная диаграмма для системы Al₂O₃  SiO₂ приведена на рис. 13.5.

 

Рис. 13.4. Диаграмма фазового равновесия InAs − InP

Рис.13.5. Фазовая диаграмма Al2O3 -SiO2  [98] (латинскими буквами указаны области на фазовой диаграмме, где присутствует жидкая  L и твердая  SS фазы)

 

Для трехкомпонентных систем диаграммы строят в трехмерном пространстве, а диаграммы с числом компонентов, большим трех, требуют специальных сложных приемов построения. Если параметром является также давление, то для двухкомпонентных систем диаграммы являются трехмерными.

С помощью диаграммы фазового равновесия для данных условий можно определить следующее: 1) число фаз в системе; 2) относительное количество каждой из фаз; 3) состав каждой фазы и ее природу (чистый компонент, раствор, соединение); 4) характер фазовых превращений.

Надо иметь в виду, что диаграмма фазового равновесия не дает информации об атомном строении фаз и их кристаллической решетке. Это самостоятельный вопрос, знание которого важно для характеристики системы и понимания свойств фаз. Диаграмма может считаться полностью достоверной, если с помощью рентгеноструктурного анализа или иных методов расшифровано атомное строение каждой из твердых фаз данной системы.

Главными методами построения диаграмм сейчас являются методы физико-химического анализа, основы которого были разработаны академиком Н. С. Курнаковым и его школой. Физико-химический анализ базируется на изучении функциональной зависимости между значениями физических свойств и параметрами концентрации, температуры и давления (X, T, p). Знание этих зависимостей позволяет устанавливать физико-химическую природу фаз и границы их существования.

Для построения диаграмм фазового равновесия используют различные экспериментальные методы, такие как термографический, микрорентгеноспектральный, рентгеноструктурный, дилатометрический и другие методы анализа. Уравнение Клапейрона — Клаузиуса — термодинамическое уравнение, относящееся к квазистатическим (равновесным) процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, полиморфное превращение и др.). Согласно уравнению, теплота фазового перехода (например, теплота испарения, теплота плавления) при квазистатическом процессе определяется выражением

где   — удельная теплота фазового перехода,   — изменение удельного объёма тела при фазовом переходе.

Уравнение названо в честь его авторов, Рудольфа Клаузиуса и Бенуа Клапейрона.
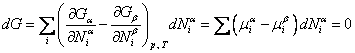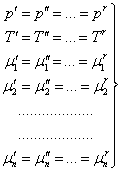