[Править]Показатель политропы

Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде:

где р — давление, V — объем газа, n — «показатель политропы».

. Здесь   — теплоёмкость газа в данном процессе,   и   — теплоемкости того же газа, соответственно, при постоянном давлении и объеме.

В зависимости от вида процесса, можно определить значение n:

• Изотермический процесс:  , так как 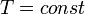 , значит, по закону Бойля — Мариотта  , и уравнение политропы вынуждено выглядеть так:  .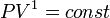

• Изобарный процесс: 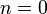 , так как 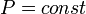 , и уравнение политропы вынуждено выглядеть так:  .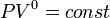

• Адиабатный процесс: 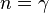  (здесь  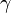 — показатель адиабаты), это следует из уравнения Пуассона.

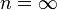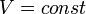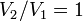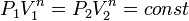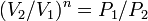• Изохорный процесс:  , так как  , и в процессе  , а из уравнения политропы следует, что  , то есть, что  , то есть  , а это возможно, только если 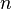  является бесконечным.

54.

Круговые обратимые и необратимые процессы

Прежде чем переходить к изложению второго закона термодинамики, рассмотрим круговые процессы. Круговым процессом, или циклом, называется такой процесс, в результате которого термодинамическое тело возвращается в исходное состояние. В диаграммах состояния P, V и других круговые процессы изображается в виде замкнутых кривых (рис. 5.1). Это связано с тем, что в любой диаграмме два тождественных состояния (начало и конец кругового процесса) изображаются одной и той же точкой на плоскости. Рис. 5.1 Рис. 5.2        Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1 – 2) и сжатия (2 – 1) газа. Работа расширения (определяется площадью фигуры 1a2V2V11) положительна ( ), работа сжатия (определяется площадью фигуры 2b1V1V22) отрицательна (dV < 0). Следовательно, работа, совершаемая за цикл, определяется площадью, охваченной замкнутой кривой. Если за цикл совершается положительная работа   .   (5.1.1) (цикл протекает по часовой стрелке), то он называется прямым (рис. 5.1). Если за цикл совершается отрицательная работа   .   (5.1.2) (цикл протекает против часовой стрелки), то он называется обратным (рис. 5.2).        Круговые процессы лежат в основе всех тепловых машин: двигателей внутреннего сгорания, паровых и газовых турбин, паровых и холодильных машин и т. д.        В результате кругового процесса система возвращается в исходное состояние, и следовательно полное изменение внутренней энергии газа равно нулю. Поэтому первое начало термодинамики для кругового процесса   .   (5.1.3) т.е. работа, совершаемая за цикл, равна количеству полученной извне теплоты. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому   .   (5.1.4) где Q1 – количество теплоты, полученное системой; Q2 – количество теплоты, отданное системой.        Поэтому термический коэффициент полезного действия для кругового процесса   .   (5.1.5)       Все термодинамические процессы, в том числе и круговые, делят на две группы: обратимые и необратимые.        Процесс называют обратимым, если он протекает таким образом, что после окончания процесса он может быть проведен в обратном направлении через все те же промежуточные состояния, что и прямой процесс. После проведения кругового обратимого процесса никаких изменений в среде, окружающей систему, не произойдет. При этом под средой понимается совокупность всех не входящих в систему тел, с которыми система непосредственно взаимодействует.        Процесс называется необратимым, если он протекает так, что после его окончания систему нельзя вернуть в начальное состояние через прежние промежуточные состояния.Нельзя осуществить необратимый круговой процесс, чтобы нигде в окружающей среде не осталось никаких изменений.        Свойством обратимости обладают только равновесные процессы. Каждое промежуточное состояние является состоянием термодинамического равновесия, нечувствительного к тому, идет ли процесс в прямом или обратном направлении.        Например, обратимым можно считать процесс адиабатического расширения или сжатия газа. При адиабатическом процессе условие теплоизолированности системы исключает непосредственный теплообмен между системой и средой. Поэтому, производя адиабатическое расширение газа, а затем сжатие, можно вернуть газ в исходное состояние так, что в окружающей среде никаких изменений не произойдет. Конечно, в реальных условиях, и в этом случае, всегда имеется некоторая необратимость процесса, обусловленная, например, несовершенством теплоизоляции, трением при движении поршня и т.д.        Только в обратимых процессах теплота используется по назначению, не расходуется зря. Если процесс неравновесный, то будет необратимый переход, т.е. часть энергии уйдет (необратимо).        Максимальным КПД обладают машины, у которых только обратимые процессы.        Реальные процессы сопровождаются диссипацией энергии (из-за трения, теплопроводности и т.д.), которая нами не рассматривается. Обратимые процессы – это в какой-то степени идеализация реальных процессов. Их рассмотрение важно по двум причинам: многие процессы в природе и технике практически обратимы; обратимые процессы являются наиболее экономичными и приводят к максимальному значению термического коэффициента полезного действия тепловых двигателей.        Доступны следующие дополнительные демонстрации:  1. Гидравлическая машина.   2. Гидростатическое давление.

  Второе начало термодинамики. Запрещая вечный двигатель 1-го рода, первое начало Термодинамика не исключает возможности создания такой машины непрерывного действия, которая была бы способна превращать в полезную работу практически всю подводимую к ней теплоту (так называемый вечный двигатель 2-го рода). Однако весь опыт по конструированию тепловых машин, имевшийся в начале 19 в., указывал на то, что кпд этих машин (отношение затраченной теплоты к полученной работе) всегда существенно меньше единицы: часть теплоты неизбежно рассеивается в окружающую среду. С. Карно первым показал (1824), что это обстоятельство имеет принципиальный характер, то есть любая тепловая машина должна содержать помимо нагревателя (источника теплоты) и рабочего тела, совершающего термодинамический цикл (например, пара), также и холодильник, имеющий температуру, обязательно более низкую, чем температура нагревателя. Второе начало термодинамики представляет собой обобщение вывода Карно на произвольные термодинамические процессы, протекающие в природе. Р. Клаузиус (1850) дал 2-му началу следующую формулировку: теплота не может самопроизвольно перейти от системы с меньшей температурой к системе с большей температурой. Независимо в несколько иной форме этот принцип высказал У. Томсон (Кельвин) в 1851: невозможно построить периодически действующую машину, вся деятельность которой сводилась бы к поднятию некоторого груза (совершению механической работы) и соответствующему охлаждению теплового резервуара. Несмотря на качественный характер этого утверждения, оно приводит к далеко идущим количественным следствиям.   Прежде всего оно позволяет определить максимальный кпд тепловой машины. Если машина работает на основе Карно цикла, то на протяжении изотермического контакта с нагревателем (Т = T₁) рабочее тело получает количество теплоты DQ₁, а на другом изотермическом участке цикла, находясь в контакте с холодильником (Т = Т₂), отдаёт ему количество теплоты D Q₂. Отношение DQ₂/DQ₁ должно быть одним и тем же у всех машин с обратимым циклом Карно, у которых одинаковы соответственно температуры нагревателей и холодильников, и не может зависеть от природы рабочего тела. Если бы это было не так, то машину с большей величиной указанного отношения можно было бы заставить работать в обратном направлении (поскольку циклы обратимы), приводя её в действие с помощью машины с меньшей величиной отношения. Эта комбинированная машина обладала бы тем свойством, что в ней теплота от холодильника передавалась бы нагревателю без совершения работы. Согласно 2-му началу Термодинамика это невозможно, и поэтому отношение DQ₂ /DQ₁ у обеих машин должно быть одинаковым. В частности, оно должно быть тем же, что и в случае, когда рабочим телом является идеальный газ. Здесь это отношение легко может быть найдено, и, таким образом, оказывается, что для всех обратимых циклов Карно .     (3) Это выражение называется пропорцией Карно. В результате для всех машин с обратимым циклом Карно кпд максимален и равен h= (T₁ — T₂)/T₁. В случае, если цикл необратим, то кпд оказывается меньше этой величины. Необходимо подчеркнуть, что пропорция Карно и кпд цикла Карно имеют указанный вид только в том случае, если температура измерена в абсолютной температурной шкале. Пропорция Карно положена в основу определения абсолютной температурной шкалы (см. Температурные шкалы). Следствием 2-го начала Термодинамика (пропорции Карно) является существование энтропии как функции состояний. Если ввести величину S, изменение которой при изотермическом обратимом сообщении системе количества теплоты DQ есть DS = DQ/T, то полное приращение S в цикле Карно будет равно нулю; на адиабатических участках цикла DS = 0 (так как DQ = 0), а изменения на изотермических участках компенсируют друг друга. Полное приращение S оказывается равным нулю и при осуществлении произвольного обратимого цикла, что доказывается разбиением цикла на последовательность бесконечно тонких циклов Карно (с малыми изотермическими участками). Отсюда следует (как и в случае внутренней энергии), что энтропия Sявляется функцией состояния системы, то есть изменение энтропии не зависит от пути перехода. Используя понятие энтропии, Клаузиус (1876) показал, что исходная формулировка 2-го начала Термодинамика полностью эквивалентна следующей: существует функция состояния системы, её энтропия S, приращение которой при обратимом сообщении системе теплоты равно dS = dQ/T;     (4) при реальных (необратимых) адиабатических процессах энтропия возрастает, достигая максимальное значения в состоянии равновесия.    Термодинамические потенциалы. Определение энтропии позволяет написать следующие выражения для дифференциалов внутренней энергии и энтальпии:    dU = TdS – pdV, dH = TdS + Vdp. (5) Отсюда видно, что естественными независимыми параметрами состояния для функций U и Н являются соответственно пары S, V и S, р. Если же вместо энтропии в качестве независимого параметра используется температура, то для описания системы более удобны свободная энергия (Гельмгольцева энергия, или изохорно-изотермический потенциал) F= U — TS (для переменных Т и V) и термодинамический потенциал G = Н — TS для переменных Т и р (Гиббсова энергия,или изобарно-изотермический потенциал), дифференциалы которых равны    dF = – SdT – pdV, dG = –SdT + Vdp. (6) Функции состояний U, Н, F и G называются потенциалами термодинамическими системы для соответствующих пар независимых переменных. Метод термодинамических потенциалов (Дж. Гиббс, 1874—1878), основанный на совместном применении 1-го и 2-го начал Термодинамика, позволяет получить ряд важных термодинамических соотношений между различными физическими свойствами системы. Так, использование независимости вторых смешанных производных от порядка дифференцирования приводит к связи между теплоёмкостями с_р и c_v, коэффициентом теплового расширения   и изотермическим коэффициентом сжатия  к соотношению между изотермическим и адиабатическим коэффициентами сжатия   и т. п. Из условия, что изолированная система в равновесном состоянии обладает максимальным значением энтропии, вытекает условие минимальности термодинамических потенциалов в равновесном состоянии по отношению к произвольным малым отклонениям от равновесия при фиксированных значениях соответствующих независимых переменных. Это приводит к важным неравенствам (условиям устойчивости), в частности     , c_p > c_v > 0 (см. Устойчивость термодинамическая).