Уравнение Пуассона для идеального газа [править]Адиабата Пуассона
Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением[6][15][16]
где 
—
его объём, 
— показатель
адиабаты, 
и 
— теплоёмкости газа
соответственно при постоянном давлении
и постоянном объёме.
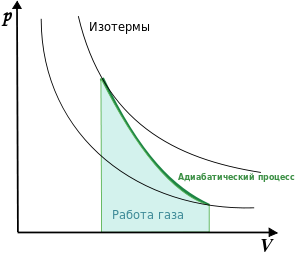
График
адиабаты (жирная линия) на 
диаграмме
для газа.
—
давление газа;
—
объём.
С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду
где 
— абсолютная
температура газа.
Или к виду
Поскольку 
всегда
больше 1, из последнего уравнения следует,
что при адиабатическом сжатии (то есть
при уменьшении
)
газ нагревается (
возрастает),
а при расширении — охлаждается, что
всегда верно и для реальных газов.
Нагревание при сжатии больше для того
газа, у которого больше коэффициент
.
[Править]Вывод уравнения
Согласно закону Менделеева — Клапейрона[6] справедливо соотношение
где R — универсальная газовая постоянная. Продифференцировав обе части, получаем
-
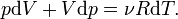
(3)
Если
в (3) подставить 
из (2),
а затем 
из (1),
получим
или, введя коэффициент :
.
Это уравнение можно переписать в виде
что после интегрирования даёт уравнение
.
Окончательно получаем
что и требовалось доказать.
[Править]Показатель адиабаты
Основная статья: Показатель адиабаты
При
адиабатическом процессе показатель
адиабаты равен 
.
Для
нерелятивистского невырожденного
одноатомного идеального газа 
[19],
для двухатомного 
[19],
для трёхатомного 
,
для газов, состоящих из более сложных
молекул, показатель адиабаты
определяется
числом степеней
свободы (i)
конкретной молекулы, исходя из
соотношения 
.
Для реальных газов показатель адиабаты отличается от показателя адиабаты для идеальных газов, особенно для низких температур, когда большую роль начинает играть межмолекулярное взаимодействие. Для его теоретического нахождения следует проводить расчёт без некоторых допущений, в частности, использованных при выводе формулы (1) и использовать формулу (1а).
Один
из методов для экспериментального
определения показателя был предложен
в 1819 г. Клеманом и Дезормом. Стеклянный
баллон вместимостью несколько литров
наполняется исследуемым газом при
давлении 
.
Затем открывается кран, газ адиабатически
расширяется, и давление падает до
атмосферного — 
.
Затем происходит его изохорноенагревание
до температуры окружающей среды. Давление
повышается до 
.
В результате такого эксперимента k можно
вычислить как[20]
Политропный процесс
[править]
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 февраля 2012; проверки требуют 11 правок.
Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной.
В
соответствии с сущностью понятия
теплоёмкости 
,
предельными частными явлениями
политропного процесса являются изотермический
процесс (
)
и адиабатный
процесс (
).
В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными ?.