51. 3. Первое начало термодинамики

Первое начало термодинамики обычно формулируется в виде утверждения:

При переходе из состояния 1 в состояние 2 поглощенное телом тепло расходуется на совершение механической работы и увеличение внутренней энергии системы: 

(3)

(  - изменение внутренней энергии системы).

Все входящие в данное соотношение величины могут принимать положительные и отрицательные значения: тепло   положительно, если оно поглощается системой, и отрицательно, если оно отдается; работа   положительна, если она совершается системой над внешними телами, и отрицательна, если работа совершается над системой; изменение внутренней энергии положительно, если поглощенное тепло больше, чем совершенная работа, если же тепла поглощается меньше, чем производится работы (например, при адиабатическом расширении), то внутренняя энергия системы уменьшается:  .

Проанализируем смысл сделанного утверждения.

Во-первых, оно означает введение новой величины - внутренней энергии системы, которая может увеличиваться или  уменьшаться в зависимости от соотношения поглощенного тепла и произведенной работы.

Во-вторых, в нем содержится так называемый принцип эквивалентности тепла и механической работы. Этот принцип заключается в том, что тепло и работа являются различными формами энергообмена системы с окружающей средой. Одно и то же изменение внутренней энергии системы может быть достигнуто за счет совершения работы без поглощения или выделения тепла (в адиабатическом процессе) либо за счет теплообмена без совершения работы (в изохорном процессе). В результате поглощения тепла система может совершать полезную работу, и наоборот - внешняя работа при определенных условиях может приводить к выделению системой тепла. Эквивалентность тепла и работы с сегодняшних позиций представляется очевидной. Действительно, нагревание тел в результате трения было известно с первобытных времен. Однако ясное научное понимание взаимосвязи тепловых и механических явлений было достигнуто лишь к середине прошлого столетия.

В-третьих, первое начало термодинамики представляет собой обобщенный закон сохранения энергии, который утверждает, что во всех процессах перехода энергии из тепловой формы в механическую и наоборот разница между поглощенным теплом и произведенной работой в точности покрывается изменением внутренней энергии системы.

Первое начало термодинамики впервые было сформулировано в работе Р. Майера (1841 г.), которая, однако, стала известной лишь после появления работ Джоуля, Клаузиуса и Гельмгольца. Наиболее значительный вклад в экспериментальную проверку первого начала внес Д. Джоуль, который с поразительной для того времени точностью определил механический эквивалент тепла, то есть установил соотношение между единицами измерения тепла и работы. Используемая в настоящее время так называемая международная калория содержит 4,1868 Дж.

Приведенная выше формулировка первого начала термодинамики не является полной. Для того, чтобы сделать к ней необходимое дополнение, рассмотрим следующую задачу.

Идеальный газ переходит из состояния 1 в состояние 2 (давление   , объем  ) двумя способами: в первом способе вначале происходит расширение газа при постоянном давлении, а затем - уменьшение давления при постоянном объеме; во втором способе, наоборот, сначала уменьшается давление при постоянном объеме, а затем происходит изобарное расширение (рис. 3). Найти поглощенное тепло, совершенную работу и изменение внутренней энергии в каждом из способов.

 

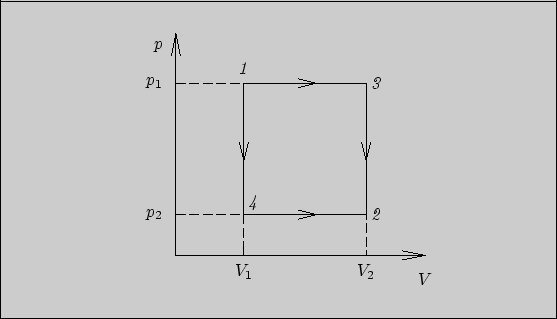
Рис. 3 

Решение. Из рисунка видно, что впервом способе переход системы из состояния 1 в состояние 2 осуществляется через промежуточное состояние 3, во втором способе - через состояние 4. Работа в первом способе равна 

во втором способе - 

При вычислении поглощенного тепла будем для простоты считать, что количество газа - один моль. Тогда в первом способе поглощенное тепло составляет 

во втором способе - 

Для молярных теплоемкостей   и   идеального газа существует известное соотношение Майера: 

где   - универсальная газовая постоянная. Пользуясь этим соотношением и уравнением состояния идеального газа 

выразим   и   через данные в задаче значения давлений и объемов: 

Для изменения внутренней энергии, используя уравнение первого начала термодинамики (3), в том и другом случае получаем 

Из рассмотренной задачи можно сделать два вывода.

1. Поглощенное тепло и совершенная работа зависят не только от начального и конечного состояний системы, но и от способа перехода (такие величины называются функциями процесса; к функциям процесса из известных нам величин относится также теплоемкость).

2. Изменение внутренней энергии в данном случае, то есть для идеального газа и данного набора процессов, оказалось зависящим только от параметров начального и конечного состояний (  ) и не зависящим от способа перехода.

В молекулярной физике второй вывод легко обобщить на любые системы и любые процессы. Действительно, если представлять внутреннюю энергию как среднее значение полной механической энергии всех частиц системы, то ясно, что это значение не должно зависеть от способа перехода системы в данное термодинамическое состояние.

В аксиоматической термодинамике обобщение второго вывода из нашей задачи на случай произвольной системы и произвольных процессов имеет характер постулата, который и является необходимым дополнением формулировки первого начала термодинамики, данной в начале параграфа. С учетом этого первое начало можно сформулировать следующим образом.

Термодинамическому состоянию системы соответствует определенное значение ее внутренней  энергии, которое может увеличиваться при поглощении системой тепла либо при совершении над ней работы: 

Обратим внимание, что данная формулировка определяет не само значение внутренней энергии, а ее изменение при переходе из состояния 1 в состояние 2. Таким образом, сама внутренняя энергия системы   определяется с точностью до произвольного постоянного слагаемого.

Величины, значение которых определяется термодинамическим состоянием системы и не зависит от способа перехода системы в это состояние, называются функциями или параметрами состояния. К параметрам состояния относятся температура, давление, объем, масса, плотность системы.

Выше говорилось, что тепло, поглощенное однородной системой, делится между ее частями в отношении их масс (в состоянии равновесия). Иными словами, поглощенное системой тепло складывается из порций тепла, поглощенного частями системы (при такой формулировке однородности системы и равновесия между ее частями не требуется). Аналогичным свойством обладает работа системы. Это можно пояснить следующим образом. Мысленно разобьем столб газа под поршнем (см. рис. 1) вертикальной стенкой на две части. К каждой из этих частей будет относиться все сказанное о целом столбе. Тогда 

то есть работа в результате сдвига поршня на   складывается из работ двух частей столба газа. То же справедливо при разбиении на произвольное количество частей.

Из этих рассуждений с учетом первого начала термодинамики вытекает свойство аддитивности внутренней энергии системы: внутренняя энергия системы складывается из внутренних энергий ее частей (подсистем).

Свойство аддитивности внутренней энергии позволяет обобщить первое начало термодинамики на задачи, в которых учитывается обмен веществом между системами. Для этого нужно порции вещества, участвующие в обмене, представлять как отдельные части системы и применять к ним первое начало термодинамики как к системам.

И конспект

52. Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплоты δQ, полученного телом, к соответствующему приращению его температуры δT:

Единица измерения теплоёмкости в системе СИ — Дж/К.

ТЕПЛОЕМКОСТЬ, кол-во теплоты, затрачиваемое для изменения т-ры на 1 °С. Согласно более строгому определению, теплоемкость-термодинамич. величина, определяемая выражением:

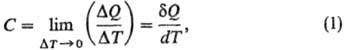
где Q- кол-во теплоты, сообщенное системе и вызвавшее изменение ее т-ры на Т. Отношение конечных разностей Q/Т наз. средней теплоемкостью, отношение бесконечно малых величин Q/dT-истинной теплоемкостью. Поскольку Q не является полным дифференциалом ф-ции состояния, то и теплоемкость зависит от пути перехода между двумя состояниями системы. Различают теплоемкость системы в целом (Дж/К), удельную теплоемкость [Дж/(г·К)], молярную теплоемкость [Дж/(моль·К)]. Во всех ниже приведенных ф-лах использованы молярные величины теплоемкости.

Из второго начала термодинамики следует, что теплоемкость пропорциональна производной от энтропии системы S по т-ре Т при постоянстве внеш. силы или термодинамич. координаты (обозначается индексом z):

Наиб. важными видами теплоемкости являются теплоемкость C_V при постоянном объеме V и теплоемкость С_р при постоянном давлении р:

С_V = (9U/9T)_V = T(9S/9T)_V, С_р = (9Н/9Т)_р = Т(9S/9Т)_р,

где U-внутр. энергия, H-энтальпия системы. Значения С_р и С_V связаны соотношением:

где  = V^-1(9V/9Т)_р-коэф. термич. расширения, x = = — V^-1(9V/9р)_T-коэф. изотермич. сжимаемости. Поскольку по условиям устойчивости фаз С_р, C_V > 0 и (9V/9р)_T < 0, то согласно (3) С_р > C_V. Это естественно, т. к. при изобарич. нагревании часть тепла, помимо увеличения внутр. энергии системы, идет на работу расширения. Для идеальных газов (9U/9V)_T = 0 и учет ур-ния состояния pV= RT приводит к соотношению: С_p - C_V = R (R-газовая постоянная). Из определений (1) и (2) следует, что для изотермич. процесса С = ,, для адиабатич. процесса С = 0.

Теплоемкость газов. Вычисление теплоемкости сводится к вычислению средней энергии теплового движения отдельных молекул, к-рое складывается из поступат. и вращат. движений молекулы как целого и из колебаний атомов внутри молекулы. Молярная теплоемкость одноатомного газа равна 3R/2 (по R/2 на каждую степень поступат. движения молекулы). теплоемкость многоатомного газа в общем случае м. б. представлена суммой вкладов от отдельных видов движения-поступательного, вращательного, колебательного.

Поступательная теплоемкость рассчитывается так же, как для одноатомного газа. Вращательная и в особенности колебательная теплоемкость должны, как правило, вычисляться на основе квантовой статистики. Согласно классич. статистике, вклады в молярную теплоемкость в расчете на одну степень свободы равны: для вращат. движения R/2, для колебат. движения R. Для большинства молекул при низких и средних т-рах колебат. степени свободы вырождены и не дают вклада в теплоемкость. Напр., теплоемкость двухатомного газа при обычных т-рах равна 5R/2. Лишь при достаточно высоких т-рах возбуждаются колебания определенной частоты.