
- •Основные понятия.
- •Основные понятия.
- •Первый закон Ньютона (закон инерции Галилея -Ньютона).
- •Второй закон Ньютона.
- •Третий закон Ньютона.
- •§ 1.2. Способы задания движения точки
- •2. Криволинейное движение
- •6. Поступательное и вращательное движения абсолютно твердого тела
- •Первый закон Ньютона (закон инерции Галилея -Ньютона).
- •Второй закон Ньютона.
- •Третий закон Ньютона.
- •Вид преобразований при коллинеарных осях[4]
- •Теорема об изменении кинетической энергии материальной точки.
- •14. Механическая система. Силы внешние и внутренние.
- •Теорема об изменении кинетической энергии системы материальных точек.
- •Сила вязкого трения
- •16. Сила упругости
- •Виды деформации твердых тел Деформация растяжения
- •Деформация сжатия
- •Деформация сдвига
- •Деформация изгиба
- •Деформация кручения
- •Пластическая и упругая деформация
- •18. Работа и потенциальная энергия
- •Абсолютно неупругий удар
- •Динамика абсолютно твердого тела
- •§1 Момент инерции. Теорема Штейнера
- •27. Движение тела переменной массы
- •Механические колебания и волны
- •30. Графический метод сложения колебаний. Векторная диаграмма. Методом вращающегося вектора амплитуды.
- •Различные формы траектории суммы колебаний. Фигуры Лиссажу.
- •31. Сложение взаимно перпендикулярных колебаний.
- •Характеристики затухающих колебаний
- •33. Вынужденные механические колебания
- •Механическая волна
- •Основные характеристики волны
- •Уравнение бегущей волны
- •Продольная и поперечная волны
- •36. Энергетические характеристики волн
- •Энергия волны
- •Уравнение стоячей волны
- •Сущность явления
- •[Править]Математическое описание
- •[Править]Релятивистский эффект Доплера
- •Движение с постоянной скоростью
- •Строгое определение
- •[Править]Объяснение
- •Преобразования Лоренца в математике
- •[Править]Определение
- •[Править]Общие свойства
- •41. Относительность одновременности
- •[Править]Сокращение линейных размеров
- •[Править]Эффект Доплера
- •[Править]Аберрация
- •42. Релятивистская динамика [править]Энергия и импульс
- •[Править]Уравнения движения
- •[Править]Преобразования энергии и импульса
- •44. Дифференциальная форма
- •Уравнение неразрывности
- •45. Закон Бернулли
- •46. Вязкость. Ламинарные и турбулентные режимы течения
- •49. Основное уравнение мкт газа
- •[Править]Идеальные газы
- •Г.А.Белуха, школа № 4, г. Ливны, Орловская обл. Работа газа в термодинамике Методические рекомендации по изучению темы, 10-й класс
- •[Править]Определение
- •51. 3. Первое начало термодинамики
- •4.4 Теплоемкость
- •Физический смысл адиабатического процесса
- •[Править]Работа газа
- •Уравнение Пуассона для идеального газа [править]Адиабата Пуассона
- •[Править]Вывод уравнения
- •[Править]Показатель адиабаты
- •Политропный процесс
- •[Править]Показатель политропы
- •55. 3.9. Закон возрастания энтропии
- •Кпд тепловой машины Карно
- •Пра́вило фаз (или правило фаз Гиббса) — соотношение, связывающее число веществ (компонентов), фаз и степеней свободы в гетерогенной системе. Уравнение Гиббса
- •Условия фазового равновесия
- •[Править]Элементарный вывод
- •58. Капиллярные явления
Г.А.Белуха, школа № 4, г. Ливны, Орловская обл. Работа газа в термодинамике Методические рекомендации по изучению темы, 10-й класс
При изучении работы газа в термодинамике учащиеся неизбежно сталкиваются с трудностями, обусловленными слабыми навыками вычисления работы переменной силы. Поэтому к восприятию этой темы необходимо готовиться, начиная уже с изучения работы в механике и решая с этой целью задачи на работу переменной силы путём суммирования элементарных работ на всём пути с помощью интегрирования.
Например, при вычислениях работы силы
Архимеда, силы упругости, силы всемирного
тяготения и т.п. надо учиться суммировать
элементарные величины с помощью
простейших дифференциальных соотношений
типа dA = Fds. Опыт
показывает, что старшеклассники легко
справляются с этой задачей, – дугу
траектории, на которой сила увеличивается
или уменьшается, нужно разбить на такие
промежутки ds, на которых
силу F можно считать постоянной
величиной, а затем, зная зависимость F = F(s),
подставить её под знак интеграла.
Например, 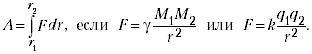
Работа этих сил вычисляется с помощью
простейшего табличного интеграла 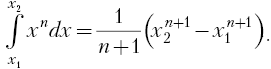
Такая методика облегчает адаптацию будущих студентов к восприятию курса физики в вузе и устраняет методические сложности, связанные с умением находить работу переменной силы в термодинамике и др.
После того как учащиеся усвоили, что такое внутренняя энергия и как найти её изменение, целесообразно дать обобщающую схему:
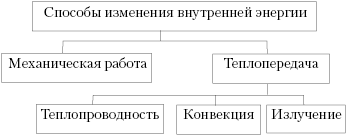
Усвоив, что работа – это один из
способов изменения внутренней энергии,
десятиклассники легко рассчитывают
работу газа в изобарном процессе. На
данном этапе необходимо подчеркнуть,
что сила давления газа на всём пути не
меняется, и по третьему закону Ньютона
|F2| = |F1|,
знак работы находим из формулы A = Fs cos![]() .
Если
= 0°,
то A > 0, если
= 180°,
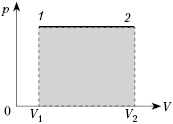
то A < 0. На графике
зависимости р(V) работа
численно равна площади под графиком.
.
Если
= 0°,
то A > 0, если
= 180°,
то A < 0. На графике
зависимости р(V) работа
численно равна площади под графиком.
Пусть газ расширяется или сжимается
изотермически. Например, газ сжимается
под поршнем, давление изменяется, и в
любой момент времени 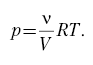
При бесконечно малом перемещении
поршня на dl мы получим
бесконечно малое изменение объёма dV,
а давление р можно считать
постоянным. По аналогии с нахождением
механической работы переменной силы,
составим простейшее дифференциальное
соотношение dA = pdV,
тогда 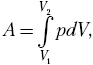 и,
зная зависимость р (V),
запишем
и,
зная зависимость р (V),
запишем 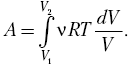 Это табличный интеграл типа
Это табличный интеграл типа 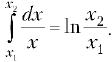 Работа газа в этом случае отрицательна,
т.к.
= 180°:
Работа газа в этом случае отрицательна,
т.к.
= 180°:
![]()
т.к. V2 < V1.
Полученную
формулу можно переписать, используя
соотношение 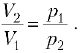
Коли́чество теплоты́ — энергия, которую получает или теряет тело при теплопередаче. Количество теплоты является одной из основныхтермодинамических величин.
Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние.
Единица измерения в Международной системе единиц (СИ): Джоуль.
[Править]Определение
Рассмотрим
систему, состоящую из двух тел ![]() и
и ![]() .
Предположим, что тело
заключено
почти полностью в жёсткую адиабатическую
оболочку, так что оно не способно
совершать макроскопическую
работу,
а обмениваться теплом (то есть энергией)
посредством микроскопических процессов
может лишь с телом
.
Предположим, что тело
также
заключено в адиабатическую оболочку
почти полностью, так что для него возможен
теплообмен лишь с
,
но не будем предполагать, что оболочка
жёсткая. Количеством
теплоты,
сообщённой телу
в
некотором процессе, будем называть
величину
.
Предположим, что тело
заключено
почти полностью в жёсткую адиабатическую
оболочку, так что оно не способно
совершать макроскопическую
работу,
а обмениваться теплом (то есть энергией)
посредством микроскопических процессов
может лишь с телом
.
Предположим, что тело
также
заключено в адиабатическую оболочку
почти полностью, так что для него возможен
теплообмен лишь с
,
но не будем предполагать, что оболочка
жёсткая. Количеством
теплоты,
сообщённой телу
в
некотором процессе, будем называть
величину ![]() ,
где
,
где ![]() —
изменение внутренней
энергии тела
.
Согласно закону
сохранения энергии,
—
изменение внутренней
энергии тела
.
Согласно закону
сохранения энергии,
![]()
где ![]() —
макроскопическая работа внешних сил
над телом
.
Если учесть, что
—
макроскопическая работа внешних сил
над телом
.
Если учесть, что
![]()
где ![]() —
работа, совершённая телом
,
то по закону сохранения энергии можно
придать форму первого
начала термодинамики:
—
работа, совершённая телом
,
то по закону сохранения энергии можно
придать форму первого
начала термодинамики:
![]()
Из
первого начала термодинамики следует
корректность введённого определения
количества теплоты, то есть независимость
соответствующей величины от выбора
пробного тела
и
способа теплообмена между телами.
Заметим, что для определения количества
теплоты необходимо пробное тело, в
противном случае первое начало теряет
смысл содержательного закона и
превращается в определение количества
теплоты (весьма бесполезное в таком
виде). При определении количества теплоты
независимо от
и ![]() первое
начало становится содержательным
законом, допускающим экспериментальную
проверку.
первое
начало становится содержательным
законом, допускающим экспериментальную
проверку.
Отметим, что, как и совершённая работа, количество переданной теплоты зависит от конкретного процесса, совершённого над телом.
