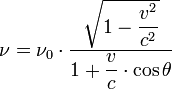- •Основные понятия.
- •Основные понятия.
- •Первый закон Ньютона (закон инерции Галилея -Ньютона).
- •Второй закон Ньютона.
- •Третий закон Ньютона.
- •§ 1.2. Способы задания движения точки
- •2. Криволинейное движение
- •6. Поступательное и вращательное движения абсолютно твердого тела
- •Первый закон Ньютона (закон инерции Галилея -Ньютона).
- •Второй закон Ньютона.
- •Третий закон Ньютона.
- •Вид преобразований при коллинеарных осях[4]
- •Теорема об изменении кинетической энергии материальной точки.
- •14. Механическая система. Силы внешние и внутренние.
- •Теорема об изменении кинетической энергии системы материальных точек.
- •Сила вязкого трения
- •16. Сила упругости
- •Виды деформации твердых тел Деформация растяжения
- •Деформация сжатия
- •Деформация сдвига
- •Деформация изгиба
- •Деформация кручения
- •Пластическая и упругая деформация
- •18. Работа и потенциальная энергия
- •Абсолютно неупругий удар
- •Динамика абсолютно твердого тела
- •§1 Момент инерции. Теорема Штейнера
- •27. Движение тела переменной массы
- •Механические колебания и волны
- •30. Графический метод сложения колебаний. Векторная диаграмма. Методом вращающегося вектора амплитуды.
- •Различные формы траектории суммы колебаний. Фигуры Лиссажу.
- •31. Сложение взаимно перпендикулярных колебаний.
- •Характеристики затухающих колебаний
- •33. Вынужденные механические колебания
- •Механическая волна
- •Основные характеристики волны
- •Уравнение бегущей волны
- •Продольная и поперечная волны
- •36. Энергетические характеристики волн
- •Энергия волны
- •Уравнение стоячей волны
- •Сущность явления
- •[Править]Математическое описание
- •[Править]Релятивистский эффект Доплера
- •Движение с постоянной скоростью
- •Строгое определение
- •[Править]Объяснение
- •Преобразования Лоренца в математике
- •[Править]Определение
- •[Править]Общие свойства
- •41. Относительность одновременности
- •[Править]Сокращение линейных размеров
- •[Править]Эффект Доплера
- •[Править]Аберрация
- •42. Релятивистская динамика [править]Энергия и импульс
- •[Править]Уравнения движения
- •[Править]Преобразования энергии и импульса
- •44. Дифференциальная форма
- •Уравнение неразрывности
- •45. Закон Бернулли
- •46. Вязкость. Ламинарные и турбулентные режимы течения
- •49. Основное уравнение мкт газа
- •[Править]Идеальные газы
- •Г.А.Белуха, школа № 4, г. Ливны, Орловская обл. Работа газа в термодинамике Методические рекомендации по изучению темы, 10-й класс
- •[Править]Определение
- •51. 3. Первое начало термодинамики
- •4.4 Теплоемкость
- •Физический смысл адиабатического процесса
- •[Править]Работа газа
- •Уравнение Пуассона для идеального газа [править]Адиабата Пуассона
- •[Править]Вывод уравнения
- •[Править]Показатель адиабаты
- •Политропный процесс
- •[Править]Показатель политропы
- •55. 3.9. Закон возрастания энтропии
- •Кпд тепловой машины Карно
- •Пра́вило фаз (или правило фаз Гиббса) — соотношение, связывающее число веществ (компонентов), фаз и степеней свободы в гетерогенной системе. Уравнение Гиббса
- •Условия фазового равновесия
- •[Править]Элементарный вывод
- •58. Капиллярные явления
[Править]Сокращение линейных размеров
Если длину (форму) движущегося объекта определять при помощи одновременной фиксации координат его поверхности, то из преобразований Лоренца следует, что линейные размеры такого тела относительно «неподвижной» системы отсчёта сокращаются:
![]() ,
,
где ![]() —
длина вдоль направления движения
относительно неподвижной системы
отсчёта, а
—
длина вдоль направления движения
относительно неподвижной системы
отсчёта, а ![]() —
длина в движущейся системе отсчёта,
связанной с телом (т.н. собственная длина
тела). При этом сокращаются продольные
размеры тела (то есть измеряемые вдоль
направления движения). Поперечные
размеры не изменяются.
—
длина в движущейся системе отсчёта,
связанной с телом (т.н. собственная длина
тела). При этом сокращаются продольные
размеры тела (то есть измеряемые вдоль
направления движения). Поперечные
размеры не изменяются.
Такое сокращение размеров ещё называют лоренцевым сокращением. При визуальном наблюдении движущихся тел дополнительно к лоренцевому сокращению необходимо учитывать время распространения светового сигнала от поверхности тела. В результате быстро движущееся тело выглядит повёрнутым, но не сжатым в направлении движения.
[Править]Эффект Доплера
Пусть
источник, движущийся со скоростью v,
излучает со скоростью света периодический
сигнал, имеющий частоту ![]() .
Эта частота измеряется наблюдателем,
связанным с источником (т.н. собственная
частота). Если этот же сигнал регистрируется
«неподвижным» наблюдателем, то его
частота
.
Эта частота измеряется наблюдателем,
связанным с источником (т.н. собственная
частота). Если этот же сигнал регистрируется
«неподвижным» наблюдателем, то его
частота ![]() будет
отличаться от собственной частоты:
будет
отличаться от собственной частоты:
,
где — угол между направлением на источник и его скоростью.
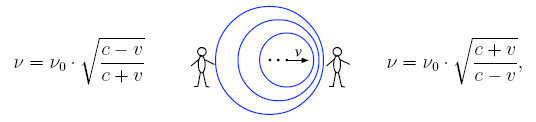
Различают
продольный и поперечный эффект
Доплера.
В первом случае
,
то есть источник и приёмник находятся
на одной прямой. Если источник движется
от приёмника, то его частота
уменьшается ![]() (красное
смещение), а если приближается, то частота
увеличивается
(красное
смещение), а если приближается, то частота
увеличивается ![]() (синее
смещение):
(синее
смещение):
Поперечный
эффект возникает, когда ![]() ,
то есть направление на источник
перпендикулярно его скорости (например,
источник «пролетает над» приёмником).
В этом случае непосредственно проявляется
эффект замедления времени:
,
то есть направление на источник
перпендикулярно его скорости (например,
источник «пролетает над» приёмником).
В этом случае непосредственно проявляется
эффект замедления времени:
Аналога поперечного эффекта в классической физике нет, и это чисто релятивистский эффект. В отличие от этого, продольный эффект Доплера обусловлен как классической составляющей, так и релятивистским эффектом замедления времени.
[Править]Аберрация
Аберрация
света является
видимым смещением объекта при относительном
движении наблюдателя и этого объекта.
Пусть в системе отсчёта S' источник света
неподвижен, и находится под углом ![]() к
оси x'. Тогда в системе S, относительно
которой система S' движется вдоль оси x
со скоростью v, направление на этот
источник света составит угол
.
В соответствии с релятивистским правилом
сложения скоростей, эти два угла связаны
следующим образом:
к
оси x'. Тогда в системе S, относительно
которой система S' движется вдоль оси x
со скоростью v, направление на этот
источник света составит угол
.
В соответствии с релятивистским правилом
сложения скоростей, эти два угла связаны
следующим образом:
![]()
где ![]() .
.
42. Релятивистская динамика [править]Энергия и импульс
Релятивистский и классический импульс, m=1
Если
частица с массой m движется со скоростью ![]() ,
то её энергия и импульс имеют следующую
зависимость от скорости:
,
то её энергия и импульс имеют следующую
зависимость от скорости:

Эти
соотношения обобщают классические
выражения для энергии и импульса,
получающиеся в результате разложения
в ряд по ![]() :
:
![]()
При
нулевой скорости энергия частицы
называется энергией покоя: ![]() .
В современной физической литературе
принято, что m —
масса частицы не
зависит от скорости, являясь инвариантом
относительно преобразований Лоренца,
и является величиной неаддитивной.
Понятие «релятивистской массы», зависящей
от скорости
.
В современной физической литературе
принято, что m —
масса частицы не
зависит от скорости, являясь инвариантом
относительно преобразований Лоренца,
и является величиной неаддитивной.
Понятие «релятивистской массы», зависящей
от скорости ![]() не
используется [25] ,
хотя оно и встречается в ранних работах
по теории относительности. Историческая
причина введения этого понятия была
связана с попытками сохранить для
релятивистского импульса классическую
форму:
не
используется [25] ,
хотя оно и встречается в ранних работах
по теории относительности. Историческая
причина введения этого понятия была
связана с попытками сохранить для
релятивистского импульса классическую
форму: ![]() .
.
При приближении скорости тела к скорости света его энергия и импульс стремятся к бесконечности. Это одна из причин, по которой «обычные» объекты не способны двигаться быстрее скорости света. Для частицы с ненулевой массой даже достижение скорости света потребует затраты бесконечной энергии. Заметные отклонения от классических выражений для энергии и импульса происходят при скоростях, близких к скорости света. Если скорости относительно невелики, то отклонения от классической динамики незначительны. Например, при скорости u=c/4 относительная разница релятивистского и классического импульса составляет всего 3%.
Между релятивистской энергией и импульсом существуют следующие связи:
![]()
Эти
формулы остаются справедливыми и для
объектов, движущихся со скоростью света.
В этом случае их масса должна быть равна
нулю ![]() .
.