
- •Основные понятия.
- •Основные понятия.
- •Первый закон Ньютона (закон инерции Галилея -Ньютона).
- •Второй закон Ньютона.
- •Третий закон Ньютона.
- •§ 1.2. Способы задания движения точки
- •2. Криволинейное движение
- •6. Поступательное и вращательное движения абсолютно твердого тела
- •Первый закон Ньютона (закон инерции Галилея -Ньютона).
- •Второй закон Ньютона.
- •Третий закон Ньютона.
- •Вид преобразований при коллинеарных осях[4]
- •Теорема об изменении кинетической энергии материальной точки.
- •14. Механическая система. Силы внешние и внутренние.
- •Теорема об изменении кинетической энергии системы материальных точек.
- •Сила вязкого трения
- •16. Сила упругости
- •Виды деформации твердых тел Деформация растяжения
- •Деформация сжатия
- •Деформация сдвига
- •Деформация изгиба
- •Деформация кручения
- •Пластическая и упругая деформация
- •18. Работа и потенциальная энергия
- •Абсолютно неупругий удар
- •Динамика абсолютно твердого тела
- •§1 Момент инерции. Теорема Штейнера
- •27. Движение тела переменной массы
- •Механические колебания и волны
- •30. Графический метод сложения колебаний. Векторная диаграмма. Методом вращающегося вектора амплитуды.
- •Различные формы траектории суммы колебаний. Фигуры Лиссажу.
- •31. Сложение взаимно перпендикулярных колебаний.
- •Характеристики затухающих колебаний
- •33. Вынужденные механические колебания
- •Механическая волна
- •Основные характеристики волны
- •Уравнение бегущей волны
- •Продольная и поперечная волны
- •36. Энергетические характеристики волн
- •Энергия волны
- •Уравнение стоячей волны
- •Сущность явления
- •[Править]Математическое описание
- •[Править]Релятивистский эффект Доплера
- •Движение с постоянной скоростью
- •Строгое определение
- •[Править]Объяснение
- •Преобразования Лоренца в математике
- •[Править]Определение
- •[Править]Общие свойства
- •41. Относительность одновременности
- •[Править]Сокращение линейных размеров
- •[Править]Эффект Доплера
- •[Править]Аберрация
- •42. Релятивистская динамика [править]Энергия и импульс
- •[Править]Уравнения движения
- •[Править]Преобразования энергии и импульса
- •44. Дифференциальная форма
- •Уравнение неразрывности
- •45. Закон Бернулли
- •46. Вязкость. Ламинарные и турбулентные режимы течения
- •49. Основное уравнение мкт газа
- •[Править]Идеальные газы
- •Г.А.Белуха, школа № 4, г. Ливны, Орловская обл. Работа газа в термодинамике Методические рекомендации по изучению темы, 10-й класс
- •[Править]Определение
- •51. 3. Первое начало термодинамики
- •4.4 Теплоемкость
- •Физический смысл адиабатического процесса
- •[Править]Работа газа
- •Уравнение Пуассона для идеального газа [править]Адиабата Пуассона
- •[Править]Вывод уравнения
- •[Править]Показатель адиабаты
- •Политропный процесс
- •[Править]Показатель политропы
- •55. 3.9. Закон возрастания энтропии
- •Кпд тепловой машины Карно
- •Пра́вило фаз (или правило фаз Гиббса) — соотношение, связывающее число веществ (компонентов), фаз и степеней свободы в гетерогенной системе. Уравнение Гиббса
- •Условия фазового равновесия
- •[Править]Элементарный вывод
- •58. Капиллярные явления
[Править]Определение
Преобразование
Лоренца (лоренцево
преобразование)
псевдоевклидова векторного
пространства ![]() —
это линейное
преобразование
—
это линейное
преобразование ![]() ,
сохраняющее индефинитноескалярное
произведение векторов.
Это означает, что для любых двух
векторов
,
сохраняющее индефинитноескалярное
произведение векторов.
Это означает, что для любых двух
векторов ![]() выполняется
равенство
выполняется
равенство
![]()
где
треугольными скобками обозначено
индефинитное скалярное произведение ![]() в
псевдоевклидовом пространстве
.
в
псевдоевклидовом пространстве
.
Аналогично, преобразование Лоренца (лоренцево преобразование) псевдоевклидова аффинного пространства — это аффинное преобразование, сохраняющее расстояние между точками этого пространства (это расстояние определяется как длина вектора, соединяющего данные точки, с помощью индефинитного скалярного произведения).
[Править]Общие свойства
Так как любое аффинное преобразование является композицией параллельного переноса (очевидным образом, сохраняющего расстояние между точками) и преобразования, имеющего неподвижную точку, то группа преобразований Лоренца аффинного пространства (группа Пуанкаре) получается из группы преобразований Лоренца векторного пространства (группа Лоренца) такой же размерности путём добавления к ней всевозможных параллельных переносов.
Если в псевдоевклидовом векторном пространстве выбран некоторый базис
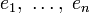 ,
то для индефинитного скалярного
произведения
определена матрица
Грама
,
то для индефинитного скалярного
произведения
определена матрица
Грама 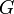 .
Тогда матрица
.
Тогда матрица 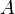 преобразования
Лоренца удовлетворяет соотношению
преобразования
Лоренца удовлетворяет соотношению
![]()
где
звёздочка означает транспонирование матрицы.
И обратно, любая матрица
,
удовлетворяющая соотношению ![]() ,
является матрицей преобразования
Лоренца. Всегда
можно выбрать базис
таким
образом, что индефинитное скалярное
произведение имеет вид
,
является матрицей преобразования
Лоренца. Всегда
можно выбрать базис
таким
образом, что индефинитное скалярное
произведение имеет вид
![]()
и
в равенстве
матрица
―
диагональная с элементами ![]() (первые
)
и
(первые
)
и ![]() (последние
(последние ![]() ).
).
Из соотношения следует, что, как и в случае ортогонального преобразования, определитель
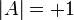 или
или 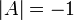 .
.Если подпространство
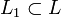 инвариантно относительно
лоренцева преобразования
инвариантно относительно
лоренцева преобразования 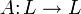 ,
то и его ортогональное (в смысле данного
индефинитного скалярного произведения)
дополнение
,
то и его ортогональное (в смысле данного
индефинитного скалярного произведения)
дополнение 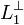 тоже
инвариантно относительно преобразования
,
причем
тоже
инвариантно относительно преобразования
,
причем 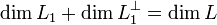 .
Однако, в отличие от ортогональных
преобразований евклидовых пространств,
равенство
.
Однако, в отличие от ортогональных
преобразований евклидовых пространств,
равенство 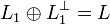 ,
где символ
,
где символ 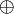 означает прямую
сумму подпространств,
вообще говоря, не имеет места (оба
подпространства
означает прямую
сумму подпространств,
вообще говоря, не имеет места (оба
подпространства 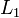 и
могут
содержать одни и те же ненулевые изотропные
векторы,
то есть
и
могут
содержать одни и те же ненулевые изотропные
векторы,
то есть 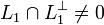 ,
так как любой изотропный вектор
ортогонален сам себе).[1]
,
так как любой изотропный вектор
ортогонален сам себе).[1]
41. Относительность одновременности
Если
два разнесённых в пространстве события
(например, вспышки света) происходят
одновременно в движущейся системе
отсчёта ![]() ,
то они будут неодновременны относительно
«неподвижной» системы
,
то они будут неодновременны относительно
«неподвижной» системы ![]() .
При
.
При ![]() из
преобразований Лоренца следует
из
преобразований Лоренца следует
![]()
Если ![]() ,
то и
,
то и ![]() .
Это означает, что, с точки зрения
неподвижного наблюдателя, левое событие
происходит раньше правого
.
Это означает, что, с точки зрения
неподвижного наблюдателя, левое событие
происходит раньше правого ![]() .
Относительность одновременности
приводит к невозможности синхронизации
часов в различных инерциальных системах
отсчёта во всём пространстве.
.
Относительность одновременности
приводит к невозможности синхронизации
часов в различных инерциальных системах
отсчёта во всём пространстве.
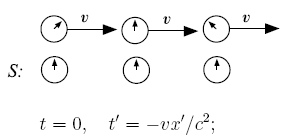
С точки зрения системы S
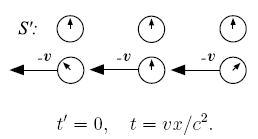
С точки зрения системы S'
Пусть в двух системах отсчёта вдоль оси x расположены синхронизированные в каждой системе часы, и в момент совпадения «центральных» часов (на рисунке ниже) они показывают одинаковое время.
Левый рисунок показывает, как эта ситуация выглядит с точки зрения наблюдателя в системе S. Часы в движущейся системе отсчёта показывают различное время. Находящиеся по ходу движения часы отстают, а находящиеся против хода движения опережают «центральные» часы. Аналогична ситуация для наблюдателей в S' (правый рисунок).
