Уравнение бегущей волны

Рассмотрим колебания источника волны, происходящие с циклической частотой ω (ω=2π⋅ν=2πT) и амплитудой A:

x(t)=A⋅sin(ω⋅t),

где x(t) — смещение источника от положения равновесия.

В некоторую точку среды колебания придут не мгновенно, а через промежуток времени, определяемый скоростью волны и расстоянием от источника до точки наблюдения. Если скорость волны в данной среде равна υ, то зависимость от времени t координаты (смещение) x колеблющейся точки, находящейся на расстоянии r от источника, описывается уравнением

x(t,r)=A⋅sinω⋅(t−rυ)=A⋅sin(ωt−kr),(1)

где k —волновое число \left(k=\frac{\omega }{\upsilon } = \frac{2\pi }{\lambda }), \;\;\; \varphi =\omega \cdot t-k\cdot r — фаза волны.

Выражение (1) называется уравнением бегущей волны.

Бегущую волну можно наблюдать при следующем эксперименте: если один конец резинового шнура, лежащего на гладком горизонтальном столе, закрепить и, слегка натянув шнур рукой, привести его второй конец в колебательное движение в направлении, перпендикулярном шнуру, то по нему побежит волна.

Продольная и поперечная волны

Различают продольные и поперечные волны.

• Волна называется поперечной, если частицы среды колеблются в плоскости, перпендикулярной направлению распространения волны.

Рассмотрим подробнее процесс образования поперечных волн. Возьмем в качестве модели реального шнура цепочку шариков (материальных точек), связанных друг с другом упругими силами (рис. 3, а). На рисунке 3 изображен процесс распространения поперечной волны и показаны положения шариков через последовательные промежутки времени, равные четверти периода.

В начальный момент времени (t1=0) все точки находятся в состоянии равновесия (рис. 3, а). Если отклонить шарик 1 от положения равновесия перпендикулярно всей цепочки шаров, то 2-ой шарик, упруго связанный с 1-ым, начнет двигаться за ним. Вследствие инертности движения 2-ой шарик будет повторять движения 1-ого, но с запаздыванием во времени. Шар 3-й, упруго связанный со 2-ым, начнет двигаться за 2-ым шариком, но с еще большим запаздыванием.

Через четверть периода (t2=T4) колебания распространяются до 4-го шарика, 1-ый шарик успеет отклониться от своего положения равновесия на максимальное расстояние, равное амплитуде колебаний А (рис. 3, б). Через полпериода (t3=T2) 1-ый шарик, двигаясь вниз, возвратится в положение равновесия, 4-ый отклонится от положения равновесия на расстояние, равное амплитуде колебаний А (рис. 3, в). Волна за это время доходит до 7-го шарика и т.д.

Через период (t5=T) 1-ый шарик, совершив полное колебание, проходит через положение равновесия, а колебательное движение распространится до 13-ого шарика (рис. 3, д). А дальше движения 1-го шарика начинают повторяться, и в колебательном движение участвуют все больше и больше шариков (рис. 3, д).

Поперечные волны вызывают звучание струн музыкальных инструментов при их возбуждении.

• Волна называется продольной, если колебания частиц среды происходят вдоль направления распространения волн.

Продольную волну легко получить с помощью длинной пружины, которая лежит на гладкой горизонтальной поверхности и один конец ее закреплен. Легким ударом по свободному концу В пружины мы вызовем появление волны (рис. 5). При этом каждый виток пружины будет колебаться вдоль направления распространения волны BC.

Примерами продольных волн являются звуковые волны в воздухе и жидкости. Упругие волны в газах и жидкостях возникают только при сжатии или разрежении среды. Поэтому в таких средах возможно распространение только продольных волн.

Волны могут распространяться не только в среде, но и вдоль границы раздела двух сред. Такие волны получили название поверхностных волн. Примером данного типа волн служат хорошо знакомые всем волны на поверхности воды.

34. Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание начнет распространяться в среде с некоторой скоростью v. Процесс распространения колебаний называется волной. Частицы среды, в которой распространяется волна, не переносятся волной, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебания частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Механические поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн. В продольных волнах вследствие совпадения направлений колебаний частиц и волны появляются сгущения и разрежения.

Распространение волн в упругой среде.

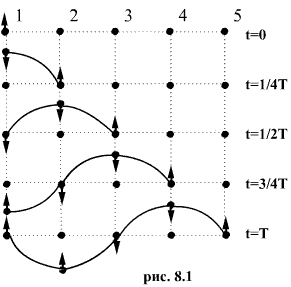
На рис.8.1 показано движение частиц при распространении в среде поперечной волны. Номерами 1,2,3 и т.д. обозначены частицы, отстоящие друг от друга на расстоянии, равном   , т.е. на расстоянии, проходимом волной за четверть периода колебаний, совершаемых частицами. В начальный момент времени (t = 0) все точки расположены на прямой и ни одна из них не выходит из положения равновесия. Приведем точку 1 в гармоническое колебание с периодом Т, направленное перпендикулярно линии 1-5. Гак как частицы среды связаны между собой силами упругости, они тоже приходят в колебания, но с некоторым запаздыванием. Через четверть периода   точка 1 отклонится от линии равновесия на максимальное смещение. Колебание начали все точки, лежащие слева от точки 2. По истечении времени  начнет подниматься вверх и точка 2. При   , первая точка вернется в положение равновесия, вторая точка достигнет максимального отклонения, и колебания дойдут до точки 3. При   точка 1 достигнет максимального отрицательного смещения, точка 2 вернется в положение равновесия и колебания достигнут точки 4. Наконец, за время, равное периоду t = Т, точка 1 вернется в положение равновесия, совершив полностью одно колебание. Колебания распространились до точки 5, все колеблющиеся точки образуют волну. При дальнейших колебаниях точек волновой процесс распространится вправо от точки 5. В рассмотренном случае образования поперечной волны каждая частица движется только вверх и вниз. У наблюдателя же создается впечатление, что «волна бежит», хотя в действительности происходит только передача движения от одной точки среды к другой.

В момент времени равный периоду (t = Т), точки 1 и 5, находящиеся в положении равновесия, имеют одинаковое смещение и одинаковое направление движения (вверх). Поэтому говорят, что точки I и 5 имеют одинаковые фазы. В отличие от этого точки 1 и 3, хотя смещения у них одинаковы, движутся в противоположные стороны, поэтому говорят, что точки 1 и 3 находятся в противоположных фазах. Расстояния между точками 1 и 5 определяет длину волны λ т.е. длиной волны λ называется, расстояние между ближайшими точками волны, колеблющимися в одинаковых фазах. Периодом волны Т называют время одного полного колебания ее точек. Величина, обратная периоду, называется частотой волны. Скорость волны определяется скоростью распространения колебаний от одной точки среды к другой:   Так как   то,

(8.1)

Скорость распространения волн тем меньше, чем инертнее среда, т.е. чем больше ее плотность. С другой стороны, она имеет большее значение в более упругой среде, чем в менее упругой. Скорость продольных волн определяется по формуле:  , а поперечной: 

где ρ- плотность среды, E - модуль Юнга, G - модуль сдвига. Так как для большинства твердых тел E>G то скорость продольных волн больше скорости поперечных.

В физике мы имеем дело с волнами различной природы: механическими, электромагнитными и т.д. Несмотря на отличия, эти волны имеют много общих черт. Волны, рассматриваемый параметр которых (смещение молекул, механическое напряжение, и т.д.) изменяется периодически вдоль оси распространения, называются продольнымиволнами. Если колебания происходят перпендикулярно оси распространения волны (как у электромагнитных волн, например), то такие волны называются поперечными. 

Если взаимосвязь между частицами среды осуществляется силами упругости, возникающими вследствие деформации среды при передаче колебаний от одних частиц к другим, то волны называются упругими. К ним относятся звуковые, ультразвуковые, сейсмические и др. волны. На первой анимации изображён процесс распространения  продольной упругой волны в решётке, состоящей из шариков, соединённых упругими пружинками. Каждый шарик колеблется по гармоническому закону в продольном направлении, совпадающем с направлением распространения волны. Амплитуда каждого шарика одинакова и равна A, а фаза колебаний линейно растёт с увеличением номера шарика на т.е.

x₀=Asin(t);  x₁=Asin(t+); x₂=Asin(t+2); x₃=Asin(t+3);  и т.д.

где  -частота волны, t - время,  - изменение фазы от шарика к шарику

В поперечной волне колебания происходят в направлении, перпендикулярном направлению распространения волны. Как и в случае продольных волн амплитуды колебаний всех шариков одинаковы, а фаза линейно изменяется от шарика к шарику

y₀=Bsin(t);  y₁=Bsin(t+); y₂=Bsin(t+2); y₃=Bsin(t+3);  и т.д.

В общем виде уравнение распространения волны может быть записано в виде: z = Acos(tkxгде z - координата, по которой происходит движение частиц, x - координата оси, вдоль которой распространяется волна, k - волновое число, равное / v, v - скорость распространения волны. Зная частоту волны и скорость её распространения, мы можем найти сдвиг фаз между соседними шариками (частицами):  / v)a, где a - расстояние между шариками в решётке.

На следующей анимации изображено наложение продольной и поперечной волн равной амплитуды, сдвинутых по фазе на 90 градусов. В результате каждая масса совершает круговые движения. Уравнение движения каждого шарика может быть описано уравнением:

x=Acos(t+_); y=Asin(t+_)

У волн, наблюдаемых на поверхности жидкости, так называемых поверхностных волн, взаимосвязь между соседними элементами поверхности жидкости при передаче колебаний осуществляется не силами упругости, а силами поверхностного натяжения и тяжести. Колебания масс в сетке моделируют движение молекул в волне на поверхности жидкости. В случае малой амплитуды волны каждая масса движется по окружности, радиус которой убывает с расстоянием от поверхности. Массы внизу сетки находятся в покое.

Волны на поверхности жидкости не являются ни продольными, ни поперечными. Как мы можем видеть на анимации, красный шарик, моделирующий молекулу поверхности жидкости, движется по круговой траектории. Таким образом, волна на поверхности жидкости представляет собой суперпозицию продольного и поперечного движения молекул.

35. Бегущая волна — волновое движение, при котором поверхность равных фаз (фазовые волновые фронты) перемещается с конечной скоростью (постоянной для однородной среды). С бегущей волной, групповая скорость которой отлична от нуля, связан перенос энергии, импульса или других характеристик процесса^[1].

Бегущая волна - волна, которая при распространении в среде переносит энергию (в отличие от стоячей волны). Примеры: упругая волна в стержне, столбе газа, жидкости, электромагнитная волна вдоль длинной линии, в волноводе^[2].

Бегущая волна — волновое возмущение, изменяющееся во времени   и пространстве   согласно выражению

где   — амплитудная огибающая волны,   — волновое число и   — фаза колебаний. Фазовая скорость   этой волны даётся выражением

где   — это длина волны.

Фазовая скорость электромагнитной волны

Коэффициент при второй производной по времени, есть величина, обратная квадрату фазовой скорости волны . Для электромагнитной волны фазовая скорость из волновых уравнений

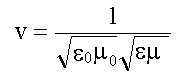
В вакууме ε = &mu = 1 и

.

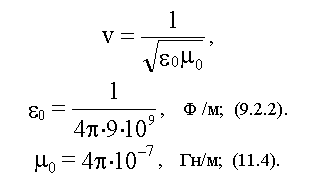Тогда:

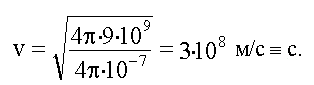
Полученное значение фазовой скорости электромагнитной волны в вакууме равно скорости света в вакууме - с. С учетом этого:

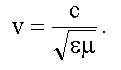Гармонические волны - простейшие решения волновых уравнений

 

Легко проверить, что

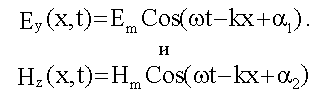
являются решениями волновых уравнений (16.1.2). Эти решения описывают электромагнитную волну, у которой вектор   направлен вдоль оси y, вектор   - вдоль оси z, волна распространяется вдоль оси x, таким образом, векторы  ,  ,   образуют правую тройку.  Связь между модулями векторов   и   электромагнитной волны и их фазами

 

Подставив решения (16.1.2.2.) в уравнения (3) и (6), получим из (3):

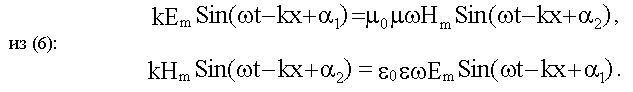
Из этих равенств следует:

1) Векторы   и   колеблются в одинаковой фазе.

 ;

2)