30. Графический метод сложения колебаний. Векторная диаграмма. Методом вращающегося вектора амплитуды.

Метод вращающегося вектора амплитуды заключается в представлении гармонического колебания с помощью вектора, длина которого равна амплитуде колебания, а направление образует с осью x угол, равный начальной фазе колебаний называют методом вращающего вектора амплитуды.

Гармонические колебания одинакового направления и частоты удобно складывать, изобразив колебания в виде векторов на плоскости - графически.

 1). Выберем некоторую направленную прямую - ось, вдоль которой будем откладывать колеблющуюся величину x .

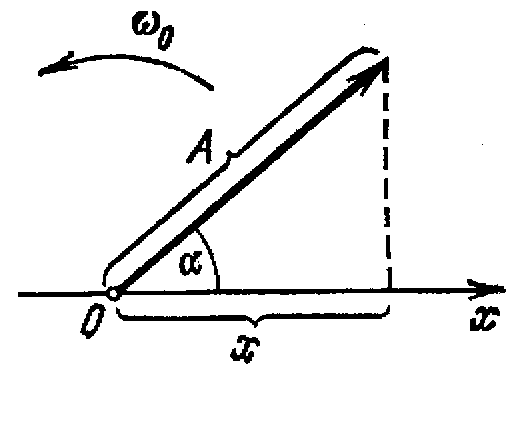
2). Из взятой на оси некоторой точки О отложим направленный отрезок - вектор длины A, образующий с осью угол некоторый α .

3). Вращая вектор А вокруг точки О с угловой скоростью ω ₀ , получим, что проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени: проекция конца вектора будет перемещаться по оси x, принимая значения от - А до + A , а координата этой проекции будет изменяться со временем по закону

Схему, полученную таким методом представления колебаний, называют векторной диаграммой .

 

 

 

Различные формы траектории суммы колебаний. Фигуры Лиссажу.

1. Разность фаз α равна нулю.

При разности фаз, равной нулю, уравнение (5) упрощается следующим образом:

Отсюда :

 - уравнение прямой.

Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой, равной  (рис. 1 а).

2. Разность фаз α равна ±π.

При разности фаз α равной ±π уравнение (5) имеет вид

- результирующее движение представляет собой гармоническое колебание вдоль прямой

 (рис. 1 б)

 

 

 

 

 

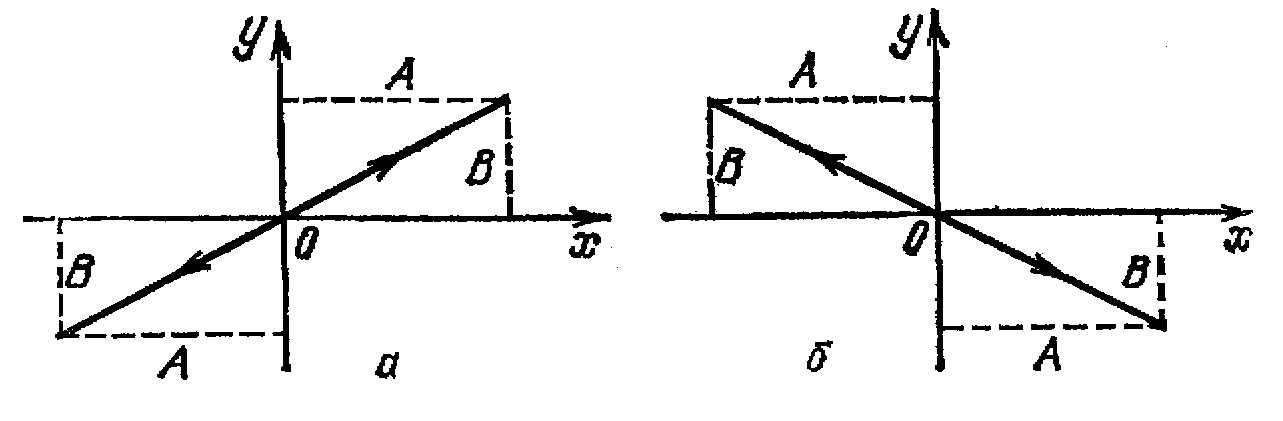
Рис.1

 

3.  Разность фаз равна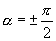 

.

Случаи   и   отличаются направлением движения по эллипсу или окружности.

При разности фаз, равной   .уравнение (5) переходит в уравнение эллипса, приведенного к координатным осям:

Полуоси эллипса равны соответствующим амплитудам колебаний. Если амплитуды А и В равны, эллипс превращается в окружность.

Равномерное движение по окружности радиуса R с угловой скоростью ω может быть представлено как сумма двух взаимно перпендикулярных колебаний:

 , 

(знак плюс в выражении для у соответствует движению против часовой стрелки, знак минус — движению по часовой стрелке).

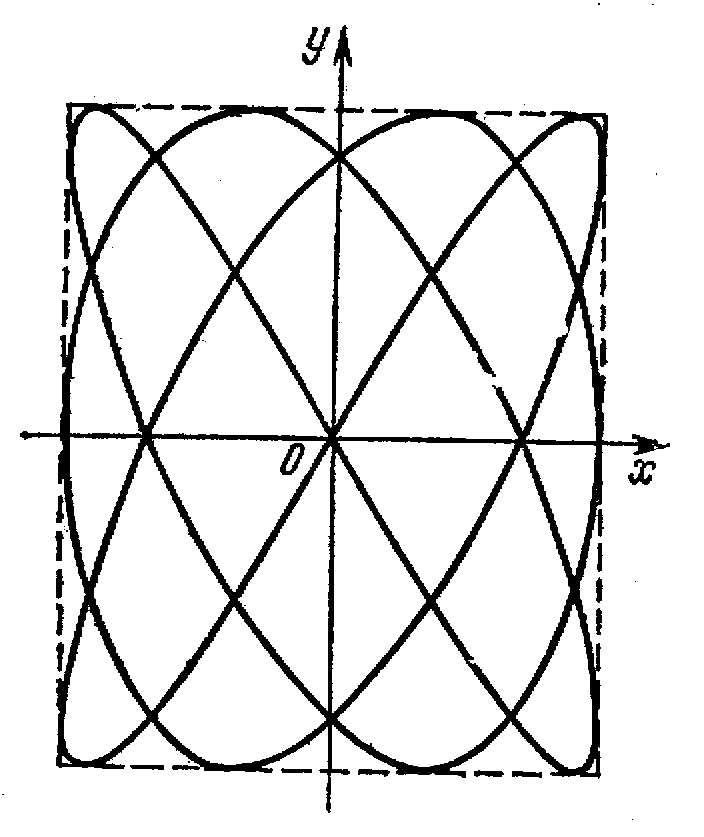
При разных частотах взаимно перпендикулярных колебаний, траектории результирующего движения будут имеют вид сложных кривых, называемых фигурами Лиссажу.

 

 

 

 

 

 

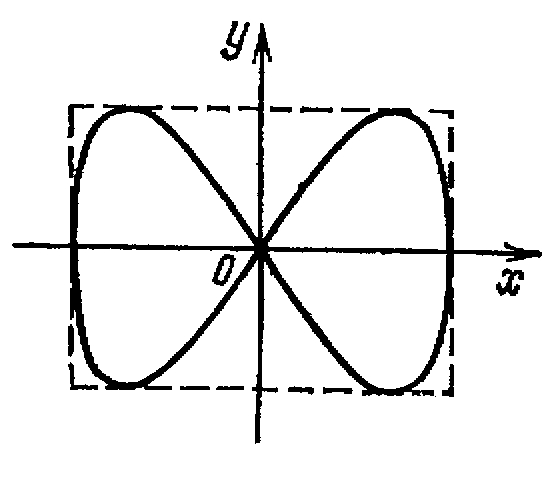
Фигура Лиссажу для

отношения частот 1:2 и

разности фаз π/2

31. Сложение взаимно перпендикулярных колебаний.

Рассмотрим две взаимно перпендикулярные векторные величины x и y , изменяющиеся со временем с одинаковой частотой ω по гармоническому закону:

   (1)

Где e _x и e _у — орты координатных осей x и y, А и B — амплитуды колебаний. Величинами x и у может быть, например, смещения материальной точки (частицы) из положения равновесия.

В случае колеблющейся частицы величины x и y можно представить в виде:

 ,   (2)

Они определяют координаты частицы на плоскости xy.

Выражения (2) представляют собой заданное в параметрической форме уравнение траектории, по которой будет двигаться частица. Вид траектории зависит от разности фаз обоих колебаний.

Исключив из уравнений (2) параметр t, получим уравнение траектории в обычном виде. Из первого уравнения:   (3). Соответственно   (4)

По формуле для косинуса суммы:

 , тогда

Преобразуем это уравнение

 (5)

Получили уравнение эллипса, оси которого повернуты относительно координатных осей х и у. Ориентация эллипса и его полуоси зависят довольно сложным образом от амплитуд A и В и разности фаз α .

Сложение колебаниё одного направления и одинаковой частоты.

Рассмотрим сложение двух гармонических колебаний х ₁ и x ₂ одного направления и одинаковой частоты:

 ,   (1)

Оба колебания представим с помощью векторов A ₁ и А ₂ . Используя правила сложения векторов можно найти результирующий вектор А, представляющий собой сумму двух векторов A ₁ и А ₂ .

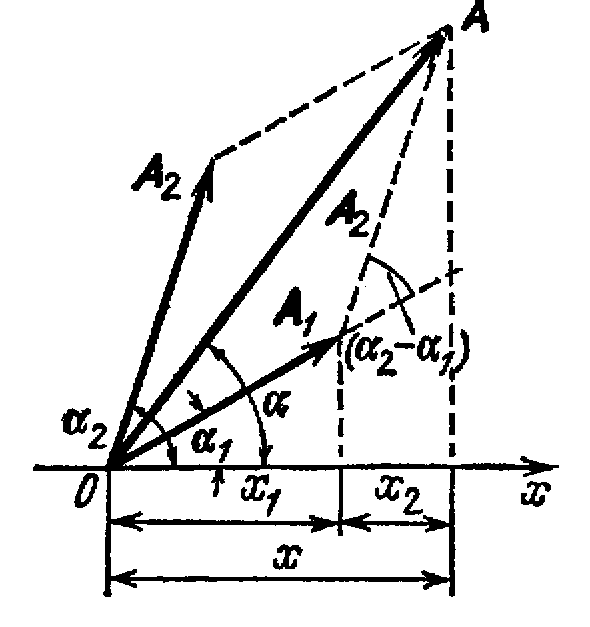 Вектор A представляет собой результирующее колебание, потому что из рисунка видно, что проекция этого вектора на ось x равна сумме проекций складываемых векторов:

Вектор A вращается с той же угловой скоростью ω ₀ , как и векторы А ₁ и А ₂ , так что сумма x ₁ и х ₂ является гармоническим колебанием с частотой (ω ₀ , амплитудой A и начальной фазой α . Используя теорему косинусов получаем, что

 

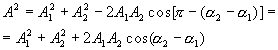 (2)

 (3)

Замена сложения функций сложением векторов, которая возможна при Представление гармонических колебаний с помощью векторов, значительно упрощает вычисления.

32.

Свободные затухающие механические колебания

Все реальные колебания являются затухающими. Энергия механических колебаний постепенно расходуется на работу против сил трения и амплитуда колебаний постепенно уменьшается (затухает).       Во многих случаях в первом приближении можно считать, что при небольших скоростях силы, вызывающие затухание колебаний, пропорциональны величине скорости (например маятник). Тогда сила трения (или сопротивления)  ,       где r – коэффициент сопротивления,   – скорость движения.       Запишем второй закон Ньютона для затухающих прямолинейных колебаний вдоль оси x:  ,       где kx – возвращающая сила, rυx – сила трения. Это уравнение можно переписать:  , отсюда следует:   .       Введем обозначения:     ;     .       Тогда однородное дифференциальное уравнение второго порядка, описывающее затухающее колебательное движение, запишем так:   .  (3.1.1)         Решение уравнения (3.1.1) имеет вид (при  ):   .  (3.1.2)         Здесь А0 и φ0 определяются из краевых условий задачи (начальных и граничных), а β и ω – из самого уравнения.       Найдем круговую частоту ω. Здесь она уже не равна  .       Для этого найдем первую и вторую производные от x:  ,               Подставим эти значения в (3.1.1) и сократим на  :  .       Сократим на   и выразим ω:  ,         ,       где ω0 – круговая частота собственных колебаний (без затухания);       ω – круговая частота свободных затухающих колебаний. Из этого выражения ясно, почему решение (3.1.1) будет только при  .       Для колебаний под действием различных сил (квазиупругих) значения ω, β, ω0 будут различными. Например, для колебаний под действием упругой силы  ;      ;          Затухающие колебания представляют собой непериодические колебания, так как в них не повторяется, например, максимальное значение амплитуды. Поэтому называть ω –циклической (повторяющейся, круговой) частотой можно лишь условно. По этой же причине и       называется условным периодом затухающих колебаний.