
- •Основные понятия.
- •Основные понятия.
- •Первый закон Ньютона (закон инерции Галилея -Ньютона).
- •Второй закон Ньютона.
- •Третий закон Ньютона.
- •§ 1.2. Способы задания движения точки
- •2. Криволинейное движение
- •6. Поступательное и вращательное движения абсолютно твердого тела
- •Первый закон Ньютона (закон инерции Галилея -Ньютона).
- •Второй закон Ньютона.
- •Третий закон Ньютона.
- •Вид преобразований при коллинеарных осях[4]
- •Теорема об изменении кинетической энергии материальной точки.
- •14. Механическая система. Силы внешние и внутренние.
- •Теорема об изменении кинетической энергии системы материальных точек.
- •Сила вязкого трения
- •16. Сила упругости
- •Виды деформации твердых тел Деформация растяжения
- •Деформация сжатия
- •Деформация сдвига
- •Деформация изгиба
- •Деформация кручения
- •Пластическая и упругая деформация
- •18. Работа и потенциальная энергия
- •Абсолютно неупругий удар
- •Динамика абсолютно твердого тела
- •§1 Момент инерции. Теорема Штейнера
- •27. Движение тела переменной массы
- •Механические колебания и волны
- •30. Графический метод сложения колебаний. Векторная диаграмма. Методом вращающегося вектора амплитуды.
- •Различные формы траектории суммы колебаний. Фигуры Лиссажу.
- •31. Сложение взаимно перпендикулярных колебаний.
- •Характеристики затухающих колебаний
- •33. Вынужденные механические колебания
- •Механическая волна
- •Основные характеристики волны
- •Уравнение бегущей волны
- •Продольная и поперечная волны
- •36. Энергетические характеристики волн
- •Энергия волны
- •Уравнение стоячей волны
- •Сущность явления
- •[Править]Математическое описание
- •[Править]Релятивистский эффект Доплера
- •Движение с постоянной скоростью
- •Строгое определение
- •[Править]Объяснение
- •Преобразования Лоренца в математике
- •[Править]Определение
- •[Править]Общие свойства
- •41. Относительность одновременности
- •[Править]Сокращение линейных размеров
- •[Править]Эффект Доплера
- •[Править]Аберрация
- •42. Релятивистская динамика [править]Энергия и импульс
- •[Править]Уравнения движения
- •[Править]Преобразования энергии и импульса
- •44. Дифференциальная форма
- •Уравнение неразрывности
- •45. Закон Бернулли
- •46. Вязкость. Ламинарные и турбулентные режимы течения
- •49. Основное уравнение мкт газа
- •[Править]Идеальные газы
- •Г.А.Белуха, школа № 4, г. Ливны, Орловская обл. Работа газа в термодинамике Методические рекомендации по изучению темы, 10-й класс
- •[Править]Определение
- •51. 3. Первое начало термодинамики
- •4.4 Теплоемкость
- •Физический смысл адиабатического процесса
- •[Править]Работа газа
- •Уравнение Пуассона для идеального газа [править]Адиабата Пуассона
- •[Править]Вывод уравнения
- •[Править]Показатель адиабаты
- •Политропный процесс
- •[Править]Показатель политропы
- •55. 3.9. Закон возрастания энтропии
- •Кпд тепловой машины Карно
- •Пра́вило фаз (или правило фаз Гиббса) — соотношение, связывающее число веществ (компонентов), фаз и степеней свободы в гетерогенной системе. Уравнение Гиббса
- •Условия фазового равновесия
- •[Править]Элементарный вывод
- •58. Капиллярные явления
27. Движение тела переменной массы
В
некоторых случаях тел связано с изменением
их массы, например масса ракеты уменьшается
вследствие истечения газов, образующихся
при сгорании топлива, и т. п.
Произведем
вывод уравнения движения тела переменной
массы на примере движения ракеты. Если
в момент времени t масса ракеты m, а ее
скорость v, то по истечении времени dt ее
масса уменьшится на dm и станет равной
т-dm, а скорость станет равной v+dv. Изменение
импульса системы за промежуток времени
dt
![]() где
u - скорость истечения газов относительно
ракеты. Тогда
где
u - скорость истечения газов относительно
ракеты. Тогда
![]() здесь
учтено, что dmdv - малое высшего порядка
малости по сравнению с остальными
слагаемыми. Если на систему действуют
внешние силы, то dp=Fdt,
поэтому
здесь
учтено, что dmdv - малое высшего порядка
малости по сравнению с остальными
слагаемыми. Если на систему действуют
внешние силы, то dp=Fdt,
поэтому
![]() или
или
![]() (1)
Второе
слагаемое в правой части (1) называют реактивной
силой Fp.
Если u противоположен v по направлению,
то ракета ускоряется, а если совпадает
с v, то тормозится.
Таким образом,
мы получили уравнение движения тела
переменной массы
(1)
Второе
слагаемое в правой части (1) называют реактивной
силой Fp.
Если u противоположен v по направлению,
то ракета ускоряется, а если совпадает
с v, то тормозится.
Таким образом,
мы получили уравнение движения тела
переменной массы
![]() (2)
которое
впервые было выведено И. В. Мещерским
(1859-1935).
Рассмотрим случай
отсутвтия воздействия внешних сил на
ракету. Положим в уравнении (1) F=0 и будем
считать, что скорость выбрасываемых
газов относительно ракеты постоянна
(ракета движется прямолинейно),
получим
(2)
которое
впервые было выведено И. В. Мещерским
(1859-1935).
Рассмотрим случай
отсутвтия воздействия внешних сил на
ракету. Положим в уравнении (1) F=0 и будем
считать, что скорость выбрасываемых
газов относительно ракеты постоянна
(ракета движется прямолинейно),
получим
![]() откуда
откуда
![]() Значение
постоянной интегрирования С определим
из начальных условий. Если в начальный
момент времени стартовая масса m0,
а ее скорость ракеты равна нулю, то С =
uln(m0). Следовательно,
Значение
постоянной интегрирования С определим
из начальных условий. Если в начальный
момент времени стартовая масса m0,
а ее скорость ракеты равна нулю, то С =
uln(m0). Следовательно,
![]() Это
соотношение называется формулой
Циолковского.
Выражения (2) и
(3) верны для нерелятивистских движений,
т. е. для случаев, когда скорости v и u
малы по сравнению со скоростью света в
вакууме.
Это
соотношение называется формулой
Циолковского.
Выражения (2) и
(3) верны для нерелятивистских движений,
т. е. для случаев, когда скорости v и u
малы по сравнению со скоростью света в
вакууме.
Механические колебания и волны
Колебания, рассматриваемые в разделе «Механика», называются механическими, при которых рассматриваются изменения положений, скоростей, ускорений и энергий каких-либо тел или их частей.
Силу, под действием которой происходит колебательный процесс, называют возвращающей силой.
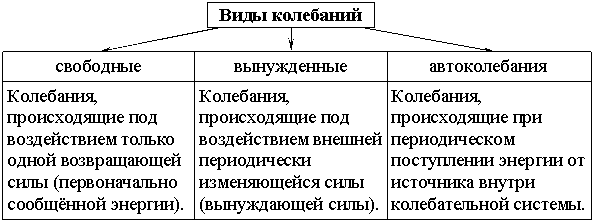
Колебания делятся также на периодические и непериодические. Непериодические колебания можно разложить на периодические, которые описываются функцией:
f(t) = f(t + nT),
где Т – период (наименьшее время повторения),
n – число колебаний.
Описать колебательный процесс – это значит выбрать параметр, зависящий от времени, и составить уравнение колебаний, решив его – получить закон колебаний.
Простейшим видом периодических колебаний являются гармонические колебания, происходящие по закону синуса или косинуса.
Гармоническая колебательная система (система тел, совершающих колебания) обычно имеет одно положение, в котором может пребывать сколь угодно долго – положение равновесия О.
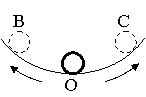
Отклонения от положения равновесия называют смещением, и обозначается Х, а наибольшее смещение (точки В или С) называется амплитудой колебания и обозначается А.
Периодические
колебания совершаются циклично. Движение
в течение одного цикла (когда тело,
пройдя все промежуточные положения,
возвращается в исходное)
называется полным
колебанием (О-С-О-В-О).
Время одного полного колебания
называется периодом
колебания (обозначается
Т). Если тело за время t совершает n полных
колебаний то ![]() ,
а
,
а ![]() и
называется частотой
колебаний.
Число колебаний за 2π единиц времени
называется циклической (круговой) частотой и
обозначается ω:
и
называется частотой
колебаний.
Число колебаний за 2π единиц времени
называется циклической (круговой) частотой и
обозначается ω:
![]()
Теперь можем дать математическую запись гармонического колебания и его графическое представление:
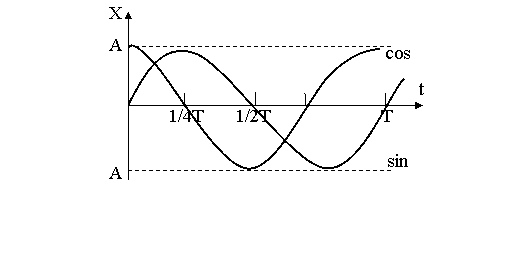
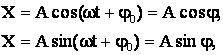
где ![]() – фаза
колебания (физическая
величина, определяющая положение
колебательной системы в данный момент
времени),
– фаза
колебания (физическая
величина, определяющая положение
колебательной системы в данный момент
времени),
φ0 – начальная фаза колебания.
При гармонических колебаниях скорость и ускорение тела также могут изменятся по закону синуса или косинуса. Однако фазы смещения Х, скорости v и ускорения a разные и описываются уравнениями:
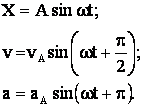
Между амплитудами смещения А, скорости vA и ускорения аА существует связь:
![]()
![]()
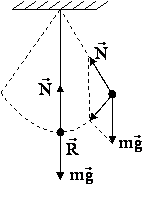
Простейшими колебательными системами являются:
а) математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания под действием силы тяжести.
Период колебания определяется уравнением:
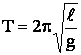 .
.
Период
Т зависит лишь от длины маятника и
местоположения (удалённости от центра
Земли или другого небесного тела),
которое определяется величиной ускорения
свободного падения 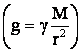 ;
;
б) пружинный маятник – материальная точка, закреплённая на абсолютно упругой пружине.
Период колебания определяется уравнением:
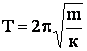 ,
,
где m – масса материальной точки,
к – коэффициент упругости пружины, определяемый из закона Гука:
![]() .
.

Характерной особенностью колебательного движения является периодическое превращение кинетической энергии тела в потенциальную и обратно.
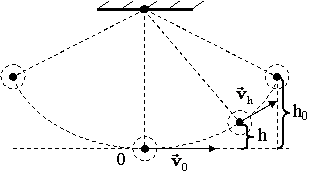
Например,
в крайнем положении тело (математический
маятник) имеет нулевую скорость и в то
же время – наибольшую высоту h0 от
горизонтали, проведённой через положение
равновесия О. Следовательно, в
этом состоянии кинетическая энергия
тела равна нулю, а потенциальная имеет
наибольшее значение, равное mgh0.
При прохождении тела через положение
равновесия имеем h =
0, а скорость тела достигнет наибольшего
значения v0.
Следовательно, потенциальная энергия
тела равна нулю, а кинетическая имеет
наибольшее значение ![]() .
В промежуточных состояниях тело имеет
и кинетическую
.
В промежуточных состояниях тело имеет
и кинетическую ![]() и
потенциальную (mgh)
энергии, сумма этих энергий равна полной
энергии колеблющегося маятника; таким
образом:
и
потенциальную (mgh)
энергии, сумма этих энергий равна полной
энергии колеблющегося маятника; таким
образом:
![]() .
.
У пружинного маятника происходит периодическое превращение кинетической энергии колеблющегося тела в потенциальную энергию деформации пружины. Сумма кинетической энергии тела и потенциальной энергии пружины остаётся при колебаниях постоянной:
![]()
где Х0 – максимальная деформация пружины в процессе колебания.
Эти формулы, выражающие закон сохранения механической энергии, применимы только в том случае, если во время колебаний не происходит превращения механической энергии в тепловую, т.е. если нет никакого трения и колебания являются незатухающими. Если же колебательное движение происходит при наличии трения, то оно будет затухающим, при котором максимальные отклонения Х0 и скорости v0 будут с течением времени уменьшаться.
Колебания, возникающие в некоторой точке пространства, за счёт того или иного взаимодействия могут передаваться от источника в разных направлениях. Процесс распространения колебания в пространстве называется волновым процессом или волной.
Вместе с колебаниями волной переносится и энергия колебаний, но сами носители этой энергии (колеблющиеся частицы среды) волной не переносятся.
В зависимости от направлений колебаний частиц среды и направления распространения волн различают волны:
1. Поперечные – в которых частицы среды колеблются перпендикулярно направлению распространения волны (волны на поверхности жидкости, в твёрдых телах).
2. Продольные – в которых частицы среды колеблются вдоль направления распространения волны (волны в газах, внутри жидкости).
Скорость, с которой распространяется возмущение в среде, называют скоростью волны vв. Расстояние, на которое распространяется волна за время, равное периоду колебаний Т (или кратчайшее расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе), называют длинной волны λв:
![]() ,
,
где ν – частота колебаний.
Необходимо отметить, что скорость волны vв зависит от свойств среды и при переходе через границу раздела сред изменяет свою величину, а частота колебаний ν зависит лишь от источника колебаний.

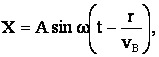
где r – расстояние от источника волн до рассматриваемой точки среды вдоль направления распространения.
Звуковыми волнами называют процесс распространения продольных механических волн в упругих средах. В разных упругих средах скорость распространения звука различна: в воздухе vзв = 340 м/с; в воде vзв = 1400 м/с; в металле vзв = 5000 м/с. Она зависит от плотности и упругости среды, в которой распространяется звук.
Громкость звука определяется переносимой волной энергией, которая пропорциональна квадрату амплитуды колебания частиц. Высота тона определяется частотой колебания частиц среды (чем больше частота колебания частиц, тем выше звук). Ухо человека воспринимает звук с частотой от 16 до 20000 Гц.
Звуковые волны с частотой колебаний частиц выше 20000 Гц называют ультразвуком. Ультразвук излучается при высокочастотных колебаниях некоторых кристаллических пластин (например, кварцевых) в переменном электрическом поле. Ультразвук широко применяется в технике, медицине и играет большую роль в жизни многих животных, которые сами излучают и улавливают ультразвуковые волны (дельфины, летучие мыши). Звуковые волны с частотой меньше 16 Гц называются инфразвуковыми.
Механические колебания
В
технике и окружающем нас мире часто
приходится сталкиваться с периодическими
(или почти периодическими) процессами,
которые повторяются через одинаковые
промежутки времени. Такие процессы
называют колебательными. К Механическими колебаниями называются движения тел, точно повторяющиеся через одинаковые промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f(t) (1). Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени. Примерами простых колебательных систем могут служить груз на пружине или математический маятник, изображенные на рисунке. |
Уравнение колебательного движения
Запишем
уравнение движения для случая
простейшего пружинного маятника,
расположенного горизонтально. Н
Пусть
сила трения пропорциональна
скорости, т.е.
Уравнение (3) – неоднородное линейное дифференциальное уравнение второго порядка, правая часть уравнения характеризует внешнее воздействие на систему.
При
отсутствии внешних сил (
и
в системе возникают свободные колебания.
При отсутствии трения уравнение
(4) упрощается:
В
этом случае полная механическая
энергия колебательной системы остается
постоянной, т.е. Решением уравнения (5) является функция вида x = xm cos (ωt> + φ0) (6). Здесь x – смещение тела от положения равновесия, xm – амплитуда колебаний, т. е. максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний, t – время. Величина, стоящая под знаком косинуса φ = ωt + φ0называется фазой гармонического процесса. При t = 0 φ = φ0, поэтому φ0 называют начальной фазой. |
Гармонические колебания Колебания, описываемые уравнением (6), являются гармоническими.
Минимальный
интервал времени, через который
происходит повторение движения тела,
называется периодом колебаний T.
Частота (величина, обратная периоду)
показывает, с На слева рисунке изображены положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить экспериментально при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Интервал времени между последовательными положениями тела равен 1/12 периода. При колебательном движении тела вдоль прямой линии (ось OX) вектор скорости направлен всегда вдоль этой прямой.
Появление слагаемого + π/2 в аргументе косинуса означает изменение начальной фазы. Максимальные по модулю значения скорости vm = ω m достигаются в те моменты времени, когда тело проходит через положения равновесия (x = 0). Аналогичным образом определяется ускорение a тела при гармонических колебаниях:
На рисунке слева приведены графики координаты, скорости и ускорения тела, совершающего гармонические колебания.
Д
Таким
свойством обладает упругая сила в
пределах применимости закона Гука:
Круговую
частоту свободных колебаний ω0 груза
на пружине можно найти из уравнения (9): Частота ω0 называется собственной частотой колебательной системы. Все физические системы (не только механические), описываемые уравнением
способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида(6). Уравнение (11) называется уравнением свободных колебаний. Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний ω0 или период T. Такие параметры процесса колебаний, как амплитуда xm и начальная фаза φ0, определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени. |
Крутильный маятник
С Это соотношение выражает закон Гука для деформации кручения. Величина μ аналогична жесткости пружины k. Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки. |
Затухающие колебания Рассмотрим колебания пружинного маятника, уравнение движения которого (согласно уравнению (4)) запишем в виде:
Первое слагаемое в данном уравнении характеризует силу трения, пропорциональную скорости маятника.
Введем
обозначения
Амплитуда и начальная фаза могут быть определены, если будут известны два значения смещения в произвольные моменты времени, т.е. так называемые начальные условия. Уравнение (14) описывает затухающие колебания.
Циклическая
частота затухающих колебаний
определяется выражением
Однако
во многих случаях, когда трение мало,
уменьшением частоты можно пренебречь,
и приближенно считать частоту свободных
колебаний равной частоте собственных
колебаний, т.е.
Характеристиками
затухающих колебаний являются
декремент затухания, определяемый из
условия
Наряду
с декрементом пользуются понятием
добротности
Затухающие
колебания происходят под действием
сил, характерных для колебательной
системы: силы упругости и силы трения.
Однако незатухающие колебания можно
получить с помощью внешних сил (см.
уравнение (3)).
Если внешняя сила периодична, то в
системе возникают колебания с частотой
изменения этой силы |
28. часть в конспекте
Величину
А называют амплитудой колебания, а
аргумент ![]() —
фазой колебания. Значение фазы при t=o т.e.
величина
—
фазой колебания. Значение фазы при t=o т.e.
величина ![]() ,
называется начальной фазой колебания.
Величина
,
называется начальной фазой колебания.
Величина ![]() есть
частота колебания. Период колебания
есть
частота колебания. Период колебания ![]() и
частота k зависят только от жесткости
пружины и от массы системы. Так как с =
Р/lст = mg/lст,
то для периода можно получить также
формулу:
и
частота k зависят только от жесткости
пружины и от массы системы. Так как с =
Р/lст = mg/lст,
то для периода можно получить также
формулу:
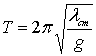
Скорость движения груза получается дифференцированием решения по t:
![]()
Для
определения амплитуды и начальной фазы
необходимо задать начальные условия.
Пусть, например, в начальный момент t =
0 положение груза x=x0 и
скоростьu=u0.
Тогда ![]()
![]() ,
откуда
,
откуда
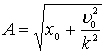 ,
,
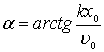
Из формул для амплитуды и начальной фазы видно, что в отличие от частоты и периода собственных колебаний они зависят от начального состояния системы. При отсутствии начальной скорости (u0=0) амплитуда А=х0, а начальная фаза a=p/2 и, таким образом,
 или
или
![]()
29.
Гармоническим
осциллятором называется система, которая
совершает колебания, описываемые
выражением вида d2s/dt2 +
ω02s
= 0 или
![]() (1)
где
две точки сверху означают двукратное
дифференцирование по времени. Колебания
гармонического осциллятора есть важный
пример периодического движения и служат
точной или приближенной моделью во
многих задачах классической и квантовой
физики. В качестве примеров гармонического
осциллятора могут быть пружинный,
физический и математический маятники,
колебательный контур (для токов и
напряжений настолько малых, что можно
было бы элементы контура считать
линейными).
1. Пружинный
маятник —
это груз массой m, который подвешен на
абсолютно упругой пружине и совершает
гармонические колебания под действием
упругой силы F = –kx, где k — жесткость
пружины. Уравнение движения маятника
имеет вид
(1)
где
две точки сверху означают двукратное
дифференцирование по времени. Колебания
гармонического осциллятора есть важный
пример периодического движения и служат
точной или приближенной моделью во
многих задачах классической и квантовой
физики. В качестве примеров гармонического
осциллятора могут быть пружинный,
физический и математический маятники,
колебательный контур (для токов и
напряжений настолько малых, что можно
было бы элементы контура считать
линейными).
1. Пружинный
маятник —
это груз массой m, который подвешен на
абсолютно упругой пружине и совершает
гармонические колебания под действием
упругой силы F = –kx, где k — жесткость
пружины. Уравнение движения маятника
имеет вид
![]() или
или
![]() Из
формулы (1) вытекает, что пружинный
маятник совершает гармонические
колебания по закону х = Асоs(ω0t+φ)
с циклической частотой
Из
формулы (1) вытекает, что пружинный
маятник совершает гармонические
колебания по закону х = Асоs(ω0t+φ)
с циклической частотой
![]() (2)
и
периодом
(2)
и
периодом
![]() (3)
Формула
(3) верна для упругих колебаний в границах,
в которых выполняется закон Гука, т. е.
если масса пружины мала по сравнению с
массой тела. Потенциальная энергия
пружинного маятника, используя (2) и
формулу потенциальной энергии предыдущего
раздела, равна
(3)
Формула
(3) верна для упругих колебаний в границах,
в которых выполняется закон Гука, т. е.
если масса пружины мала по сравнению с
массой тела. Потенциальная энергия
пружинного маятника, используя (2) и
формулу потенциальной энергии предыдущего
раздела, равна
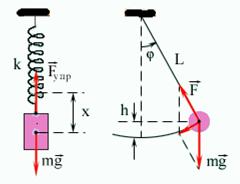
![]() 2. Физический
маятник —
это твердое тело, которое совершает
колебания под действием силы тяжести
вокруг неподвижной горизонтальной оси,
которая проходит через точку О, не
совпадающую с центром масс С тела (рис.
1).
2. Физический
маятник —
это твердое тело, которое совершает
колебания под действием силы тяжести
вокруг неподвижной горизонтальной оси,
которая проходит через точку О, не
совпадающую с центром масс С тела (рис.
1).
Если
маятник из положения равновесия отклонили
на некоторый угол α, то, используя
уравнение динамики вращательного
движения твердого тела, момент M
возвращающей силы
![]() (4)
где
J — момент инерции маятника относительно
оси, которая проходит через точку подвеса
О, l – расстояние между осью и центром
масс маятника, Fτ ≈
–mgsinα ≈ –mgα — возвращающая сила (знак
минус указывает на то, что направления
Fτ и
α всегда противоположны; sinα ≈ α поскольку
колебания маятника считаются малыми,
т.е. маятника из положения равновесия
отклоняется на малые углы). Уравнение
(4) запишем как
(4)
где
J — момент инерции маятника относительно
оси, которая проходит через точку подвеса
О, l – расстояние между осью и центром
масс маятника, Fτ ≈
–mgsinα ≈ –mgα — возвращающая сила (знак
минус указывает на то, что направления
Fτ и
α всегда противоположны; sinα ≈ α поскольку
колебания маятника считаются малыми,
т.е. маятника из положения равновесия
отклоняется на малые углы). Уравнение
(4) запишем как
![]() или
или
![]() Принимая
Принимая
![]() (5)
получим
уравнение
(5)
получим
уравнение
![]() идентичное
с (1), решение которого (1) найдем и запишем
как:
идентичное
с (1), решение которого (1) найдем и запишем
как:
![]() (6)
Из
формулы (6) вытекает, что при малых
колебаниях физический маятник совершает
гармонические колебания с циклической
частотой ω0 и
периодом
(6)
Из
формулы (6) вытекает, что при малых
колебаниях физический маятник совершает
гармонические колебания с циклической
частотой ω0 и
периодом
![]() (7)
где
введена величина L=J/(ml)
— приведенная
длина физического маятника.
Точка
О' на продолжении прямой ОС, которая
отстоит от точки О подвеса маятника на
расстоянии приведенной длины L,
называетсяцентром
качаний физического
маятника (рис. 1). Применяя теорему
Штейнера для момента инерции оси,
найдем
(7)
где
введена величина L=J/(ml)
— приведенная
длина физического маятника.
Точка
О' на продолжении прямой ОС, которая
отстоит от точки О подвеса маятника на
расстоянии приведенной длины L,
называетсяцентром
качаний физического
маятника (рис. 1). Применяя теорему
Штейнера для момента инерции оси,
найдем
![]() т.
е. ОО' всегда больше ОС. Точка подвеса О
маятника и центр качаний О' имеют свойство
взаимозаменяемости:
если точку подвеса перенести в центр
качаний, то прежняя точка О подвеса
будет новым центром качаний, и при этом
не изменится период колебаний физического
маятника.
3. Математический
маятник —
это идеализированная система, состоящая
из материальной точки массой m, которая
подвешена на нерастяжимой невесомой
нити, и которая колеблется под действием
силы тяжести. Хорошее приближение
математического маятника есть небольшой
тяжелый шарик, который подвешен на
длинной тонкой нити. Момент инерции
математического маятника
т.
е. ОО' всегда больше ОС. Точка подвеса О
маятника и центр качаний О' имеют свойство
взаимозаменяемости:
если точку подвеса перенести в центр
качаний, то прежняя точка О подвеса
будет новым центром качаний, и при этом
не изменится период колебаний физического
маятника.
3. Математический
маятник —
это идеализированная система, состоящая
из материальной точки массой m, которая
подвешена на нерастяжимой невесомой
нити, и которая колеблется под действием
силы тяжести. Хорошее приближение
математического маятника есть небольшой
тяжелый шарик, который подвешен на
длинной тонкой нити. Момент инерции
математического маятника
![]() (8)
где l —
длина маятника.
Поскольку
математический маятник есть частный
случай физического маятника, если
предположить, что вся его масса
сосредоточена в одной точке — центре
масс, то, подставив (8) в (7), найдем выражение
для периода малых колебаний математического
маятника
(8)
где l —
длина маятника.
Поскольку
математический маятник есть частный
случай физического маятника, если
предположить, что вся его масса
сосредоточена в одной точке — центре
масс, то, подставив (8) в (7), найдем выражение
для периода малых колебаний математического
маятника
![]() (9)
Сопоставляя
формулы (7) и (9), видим, что если приведенная
длина L физического маятника равна
длине l математического
маятника, то периоды колебаний этих
маятников одинаковы. Значит, приведенная
длина физического маятника —
это длина такого математического
маятника, у которого период колебаний
совпадает с периодом колебаний данного
физического маятника.
(9)
Сопоставляя
формулы (7) и (9), видим, что если приведенная
длина L физического маятника равна
длине l математического
маятника, то периоды колебаний этих
маятников одинаковы. Значит, приведенная
длина физического маятника —
это длина такого математического
маятника, у которого период колебаний
совпадает с периодом колебаний данного
физического маятника.

 олебательные
явления различной физической природы
подчиняются общим закономерностям.
Например, колебания тока в электрической
цепи и колебания математического
маятника могут описываться одинаковыми
уравнениями. Общность колебательных
закономерностей позволяет рассматривать
колебательные процессы различной
природы с единой точки зрения.
олебательные
явления различной физической природы
подчиняются общим закономерностям.
Например, колебания тока в электрической
цепи и колебания математического
маятника могут описываться одинаковыми
уравнениями. Общность колебательных
закономерностей позволяет рассматривать
колебательные процессы различной
природы с единой точки зрения.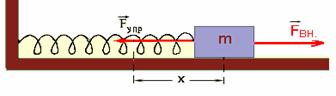 а
груз массой m,смещенный
из положения равновесия на расстояние
x, действует внешняя сила
а
груз массой m,смещенный
из положения равновесия на расстояние
x, действует внешняя сила 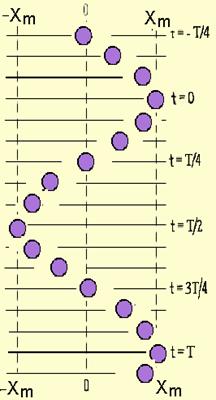 колько
колебаний совершается за единицу
времени:
.
Циклическая частота колебаний связана
с частотой и периодом колебаний T
соотношениями
колько
колебаний совершается за единицу
времени:
.
Циклическая частота колебаний связана
с частотой и периодом колебаний T
соотношениями 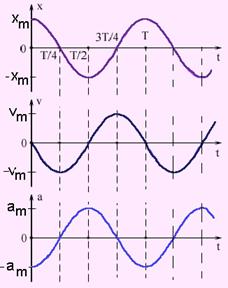 ля
того, чтобы свободные колебания
совершались по гармоническому закону,
необходимо, чтобы сила, стремящаяся
возвратить тело в положение равновесия,
была пропорциональна смещению тела
из положения равновесия и направлена
в сторону, противоположную смещению:
ля
того, чтобы свободные колебания
совершались по гармоническому закону,
необходимо, чтобы сила, стремящаяся
возвратить тело в положение равновесия,
была пропорциональна смещению тела
из положения равновесия и направлена
в сторону, противоположную смещению: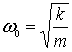 или
или  (10).
(10).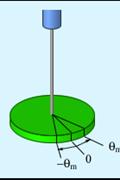 уществует
много разновидностей механических
колебательных систем, в которых
используются силы упругих деформаций.
На рисунке слева показан горизонтально
расположенный диск, висящий на упругой
нити, закрепленной в его центре масс.
При повороте диска на угол
уществует
много разновидностей механических
колебательных систем, в которых
используются силы упругих деформаций.
На рисунке слева показан горизонтально
расположенный диск, висящий на упругой
нити, закрепленной в его центре масс.
При повороте диска на угол