§1 Момент инерции. Теорема Штейнера

   Момент инерции материальной точки равен

   Моментом инерции системы относительно оси вращения называется физическая величина, равная сумме произведения масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси.

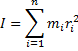
Момент инерции тела в случае непрерывного распределения массы равен

I=

-интегрируется по всему объёму.

I=

1. Найдем момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр. Разобьем диск на кольцевые слои толщиной dr. Все точки слоя будут находиться на одинаковом расстоянии от оси, равномr. Объем такого слоя равен dV=S    

Площадь кольца

S= =

I=

m=

 

2. Полый тонкостенный цилиндр радиуса R (обруч, велосипедное колесо и тому подобное).

3. Сплошной цилиндр или диск радиуса R

 

4. Прямой тонкий длиной     стержень, ось перпендикулярна стержню и проходит через его середину.

 

 

 

5. Шар радиуса R, относительно оси, проходящей через его центр.

 

 

 

  Если известен момент инерции тела относительно оси, проходящей через его центр масс, момент инерции относительно любой другой оси параллельной данной, определяется с помощью теоремы Штейнера: момент инерции тела І относительно параллельной оси вращения равен моменту инерции Іс относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы М тела на квадрат расстояния а между осями І=Іс+m

6. Момент инерции прямого стержня длиной  , ось перпендикулярна стержню и проходит через его конец.

I=

25. При вращении твёрдого тела относительно неподвижной оси, все точки тела движутся по плоским круговым траекториям. Выделим частицу m_i тела, вращающегося вокруг оси z (рис. 9.2). Положение частицы зададим радиус-вектором   относительно произвольного центра 0, лежащего на оси вращения. R_i — радиус окружности, по которой движется рассматриваемая точка.V_i = wR_i — её линейная скорость. 

Рис. 9.2

Рассматривая твёрдое тело как неизменную систему материальных точек, для каждой из них можно записать уравнение моментов:

                          .                  (9.1)

В левой части этого уравнения — момент внешних сил относительно оси z, действующий на частицу m_i. Справа — производная по времени проекции момента импульса частицы на ту же ось.

Момент импульса частицы относительно центра 0 (по определению) равен:

.

Заметим, что для всех частиц  , поэтому легко вычислить модуль этого вектора L_i:

L_i = m_ir_iV_i = m_ir_iwR_i.

Так как   образует угол a_i с осью z, то проекция этого вектора на ось z равна:

            = L_iCosa_i = m_ir_iwR_iCosa_i = m_iwR_i(r_iCosa_i) = m_iw .         (9.2)

Учитывая этот результат, перепишем уравнение (9.1) ещё раз:

                          .             (9.3)

Подобные уравнения могут быть составлены для всех точек твёрдого тела.

Просуммировав все эти уравнения, получим закон вращательного движения твёрдого тела:

или

                          .             (9.4)

Здесь:    M_z — суммарный момент всех внешних сил, вращающих твёрдое тело вокруг оси z;

     w_z — угловая скорость вращения;

       — новая характеристика твёрдого тела — его момент инерции относительно оси вращения;

     L_z = I_zw_z — момент импульса тела относительно оси z.

Если момент инерции твёрдого тела I_z не меняется, уравнению (9.4) можно придать такой вид:

                          .                  (9.5)

Здесь ε = — угловое ускорение вращающегося тела.

Уравнение (9.5) называется основным уравнением динамики для твёрдого тела, вращающегося вокруг неподвижной оси.

M_z = I_z×ε                (9.6)

Трудно не заметить сходство этого уравнения со вторым законом Ньютона для движения точки:

F_z = ma_z

Сравнивая эти два выражения, отметим, что в уравнении для вращательного движения в качества «силы» выступает момент силы, вместо линейного ускорения — угловое, вместо массы используется момент инерции I_z.

Сходство этих уравнений можно продолжить, записав их иначе (9.2)

Здесь:    L_z = I_z w_x — момент импульса тела относительно оси z,

     P_z = mV_z — проекция вектора импульса частицы на ось z.

Во вращательном движении аналогом импульса Р является момент импульса L.

Рассмотренные аналогии позволяют назвать уравнение (9.6) уравнением второго закона динамики (Ньютона) для вращательного движения:

момент внешних сил, вращающих тело вокруг данной оси, равен моменту инерции тела относительно этой оси, умноженному на угловое ускорение тела.

Вернемся ещё раз к уравнению (9.4):

.

Оно в равной степени справедливо как для твердого тела, так и для системы тел. Если момент внешних сил относительно оси z равен нулю, то момент импульса системы относительно этой же оси будет оставаться постоянным.

M_z = 0, Þ   Þ L_z = I_zw_z = сonst.

Это  закон сохранения момента импульса — аналог закона сохранения импульса замкнутой системы. Но есть между этими законами одно существенное различие. Постоянство импульса частицы (если её масса не меняется) означает неизменность её линейной скорости:

p = mV = сonst. Þ V = сonst.

Если же не меняется момент импульса тела (L_z), то это не означает постоянства угловой скорости:

L_z = I_zw = сonst.

Изменение момента инерции вращающегося тела приведёт к изменению его угловой скорости даже в случае отсутствия внешних вращающих моментов. При этом сохранится неизменным произведение I_z × w = сonst., то есть угловая скорость окажется обратно пропорциональной моменту инерции тела (системы):

.

26. Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.

Основные кинематические характеристики вращательного движения тела — его угловая скорость ( ) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:

и кинетическая энергия

где I_z — момент инерции тела относительно оси вращения.

Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерции I₁, I₂ и I₃. Вращательная энергия такой молекулы задана выражением

где ω₁, ω₂, и ω₃ — главные компоненты угловой скорости.

В общем случае, энергия при вращении с угловой скоростью   находится по формуле:

, где   — тензор инерции.

Кинетическая энергия  тела, совершающего вращательное движение

 

Кинетическая энергия материальной точки   W_k =  mv² / 2 . 

Тогда для системы материальных точек или тела     .

Используя связь линейной скорости с угловой  в виде  v_i = r_i,     получим выражение для энергии вращательного движения:

(5.20)

Замечание: При плоском движении тел (например, цилиндр скатывается по наклонной плоскости,  рис. 5.12) полная скорость

,

(5.21)

где с - центр масс (инерции).

 Полная кинетическая энергия тела равна сумме кинетической энергии поступательного движения его центра масс (центра инерции) и кинетической энергии вращательного движения тела   относительно мгновенной оси)*, т.е.

.

1. Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости дви­жения центра масс. То есть, для любой точки 

или

Таким образом, кинетическая энергия тела при поступатель­ном движении равна половине произведения массы тела на квад­рат скорости центра масс. От направления движения значение Тне зависит.