
- •Основные понятия.
- •Основные понятия.
- •Первый закон Ньютона (закон инерции Галилея -Ньютона).
- •Второй закон Ньютона.
- •Третий закон Ньютона.
- •§ 1.2. Способы задания движения точки
- •2. Криволинейное движение
- •6. Поступательное и вращательное движения абсолютно твердого тела
- •Первый закон Ньютона (закон инерции Галилея -Ньютона).
- •Второй закон Ньютона.
- •Третий закон Ньютона.
- •Вид преобразований при коллинеарных осях[4]
- •Теорема об изменении кинетической энергии материальной точки.
- •14. Механическая система. Силы внешние и внутренние.
- •Теорема об изменении кинетической энергии системы материальных точек.
- •Сила вязкого трения
- •16. Сила упругости
- •Виды деформации твердых тел Деформация растяжения
- •Деформация сжатия
- •Деформация сдвига
- •Деформация изгиба
- •Деформация кручения
- •Пластическая и упругая деформация
- •18. Работа и потенциальная энергия
- •Абсолютно неупругий удар
- •Динамика абсолютно твердого тела
- •§1 Момент инерции. Теорема Штейнера
- •27. Движение тела переменной массы
- •Механические колебания и волны
- •30. Графический метод сложения колебаний. Векторная диаграмма. Методом вращающегося вектора амплитуды.
- •Различные формы траектории суммы колебаний. Фигуры Лиссажу.
- •31. Сложение взаимно перпендикулярных колебаний.
- •Характеристики затухающих колебаний
- •33. Вынужденные механические колебания
- •Механическая волна
- •Основные характеристики волны
- •Уравнение бегущей волны
- •Продольная и поперечная волны
- •36. Энергетические характеристики волн
- •Энергия волны
- •Уравнение стоячей волны
- •Сущность явления
- •[Править]Математическое описание
- •[Править]Релятивистский эффект Доплера
- •Движение с постоянной скоростью
- •Строгое определение
- •[Править]Объяснение
- •Преобразования Лоренца в математике
- •[Править]Определение
- •[Править]Общие свойства
- •41. Относительность одновременности
- •[Править]Сокращение линейных размеров
- •[Править]Эффект Доплера
- •[Править]Аберрация
- •42. Релятивистская динамика [править]Энергия и импульс
- •[Править]Уравнения движения
- •[Править]Преобразования энергии и импульса
- •44. Дифференциальная форма
- •Уравнение неразрывности
- •45. Закон Бернулли
- •46. Вязкость. Ламинарные и турбулентные режимы течения
- •49. Основное уравнение мкт газа
- •[Править]Идеальные газы
- •Г.А.Белуха, школа № 4, г. Ливны, Орловская обл. Работа газа в термодинамике Методические рекомендации по изучению темы, 10-й класс
- •[Править]Определение
- •51. 3. Первое начало термодинамики
- •4.4 Теплоемкость
- •Физический смысл адиабатического процесса
- •[Править]Работа газа
- •Уравнение Пуассона для идеального газа [править]Адиабата Пуассона
- •[Править]Вывод уравнения
- •[Править]Показатель адиабаты
- •Политропный процесс
- •[Править]Показатель политропы
- •55. 3.9. Закон возрастания энтропии
- •Кпд тепловой машины Карно
- •Пра́вило фаз (или правило фаз Гиббса) — соотношение, связывающее число веществ (компонентов), фаз и степеней свободы в гетерогенной системе. Уравнение Гиббса
- •Условия фазового равновесия
- •[Править]Элементарный вывод
- •58. Капиллярные явления
Абсолютно неупругий удар
Абсолю́тно неупру́гий удар — удар, в результате которого компоненты скоростей тел, нормальные площадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело.
![]()
Где v это общая скорость тел, полученная после удара, ma - масса первого тела, ua - скорость первого тела до соударения. mb - масса второго тела, ub -скорость второго тела до соударения. Важно - импульсы являются величинами векторными, поэтому складываются только векторно.
![]()
Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Часть кинетической энергии соудареямых тел в результате неупругих деформаций переходит в тепловую.
Хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики.
20.
Каждой
точке потенциального поля соответствует,
с одной стороны, некоторое значение
вектора силы ![]() ,
действующей на тело, и, с другой стороны,
некоторое значение потенциальной
энергии
,
действующей на тело, и, с другой стороны,
некоторое значение потенциальной
энергии ![]() .
Следовательно, между силой и потенциальной
энергией должна существовать определенная
связь.
.
Следовательно, между силой и потенциальной
энергией должна существовать определенная
связь.

Для
установления этой связи вычислим
элементарную работу ![]() ,
совершаемую силами поля при малом
перемещении
,
совершаемую силами поля при малом
перемещении ![]() тела,
происходящем вдоль произвольно выбранного
направления в пространстве, которое
обозначим буквой
тела,
происходящем вдоль произвольно выбранного
направления в пространстве, которое
обозначим буквой ![]() .
Эта работа равна
.
Эта работа равна
![]()
где ![]() -
проекция силы
на
направление
.
-
проекция силы
на
направление
.
Поскольку
в данном случае работа совершается за
счет запаса потенциальной энергии
,
она равна убыли потенциальной энергии ![]() на
отрезке оси
:
на
отрезке оси
:
![]()
Из двух последних выражений получаем
![]()
Откуда
![]()
Последнее выражение дает среднее значение на отрезке . Чтобы
получить значение в точке нужно произвести предельный переход:
![]()
Так как может изменяться не только при перемещении вдоль оси , но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от по :
![]()
Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:
![]()
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:
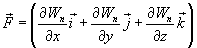
в
математике вектор 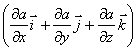 ,
,
где
а - скалярная функция х, у, z, называется
градиентом этого скаляра обозначается
символом ![]() .Следовательно
сила равна градиенту потенциальной
энергии, взятого с обратным знаком
.Следовательно
сила равна градиенту потенциальной
энергии, взятого с обратным знаком
|
Потенциа́льная я́ма – область пространства, где присутствует локальный минимум потенциальной энергии частицы.
Если в потенциальную яму попала частица, энергия которой ниже, чем необходимая для преодоления краёв ямы, то возникнут колебания частицы в яме. Амплитуда колебаний будет обусловлена собственной энергией частицы. Частица, находящаяся на дне потенциальной ямы, пребывает в состоянии устойчивого равновесия, то есть при отклонении частицы от точки минимума потенциальной энергии возникает сила, направленная в противоположную отклонению сторону. Если частица подчиняется квантовым законам, то даже несмотря на недостаток энергии она с определённой вероятностью может покинуть потенциальную яму (явлениетуннельного эффекта).
Потенциа́льный барье́р — область пространства, разделяющая две другие области с различными или одинаковыми потенциальными энергиями. Характеризуется «высотой» — минимальной энергией классической частицы, необходимой для преодоления барьера.
На приведённом изображении участок BNC является потенциальным барьером для частицы с энергией E1. Потенциальным барьером для частицы с энергией E2 служит участок от нуля до точки D, так как частица не в состоянии подойти к началу координат ближе, чем координата точки D.
В классической механике, в случае, когда частица не обладает энергией, большей максимума для данного барьера, она не сможет преодолеть потенциальный барьер. В квантовой механике, напротив, возможно преодоление барьера с определённой вероятностью (туннельный эффект).
21.
Условия потенциальности поля |
|
|
|
Пусть
Предположим, что поле A является потенциальным. Тогда существует скалярное поле φ такое, что A = grad φ. Рассмотрим скалярное произведение векторов A и dr:
Выражение
в правой части этого равенства
представляет собой полный дифференциал
функции φ (x, y, z).
Если частные производные
Учитывая, что частные производные от функции φ являются координатами вектора A, получаем следующие условия потенциальности поля A:
Эти три уравнения можно выразить одной короткой формулой: rot A = 0. Таким образом, векторное поле A является потенциальным, если ротор этого поля равен нулю. |
Потенциальное поле - это поле, в котором работа силы не зависит от формы пути, а зависит лишь от положений начальной и конечной точек траектории, а силы, действующие в нем, - консервативными.
Консервативные (потенциальные) силы - это силы, зависящие только от координат точек системы и работа которых не зависит от пути перехода из начального в конечное положение, а определяется только начальным и конечным положением.
В потенциальном поле работа сил по любому замкнутому контуру равна нулю.
Связь между силовой и энергетической характеристиками в потенциальном силовом поле.
В потенциальном силовом поле и E и F являются функциями координат. Пусть сила F направлена вдоль перемещения, тогда приращение Ep:
-dE = Fdr = Frdr
Fr = -dEp/dr
"-" указывает на то, что сила направлена в сторону убывания потенциальной энергии.
В случае, когда вектор F имеет произвольное направление в пространстве, необходимо поставить в соответствие сколярному полю Ep вектор F.
Эту задачу решает градиент:
F = - grad Ep.
Потенциальное поле не имеет замкнутых интегральных траекторий без особых точек. Потенциальное поле, удерживающее частицу в ограниченной области пространства, можно грубо моделировать потенциальной ямой бесконечной глубины. Измерение распределения потенциала в электролитической ванне, а - модель системы электродов с вращательной симметрией в электролитической ванне. / - модель электрической линзы. 2 - вода. 3 - деревянная или пластмассовая ванна. б - измерительный мостик с зондом. в - электролитическая ванна с. Потенциальное поле на поверхности электролита при этом точно совпадает с распределением потенциала полной ( неразрезанной) системы электродов в воздухе или в вакууме. За счет отбрасывания симметричной половины можно значительно увеличить размеры модели электродов и тем самым повысить точность измерений. Потенциальное поле, содержащее только валентные и деформационные силовые постоянные, называется просто валентно-силовым полем. Потенциальное поле имеет шаровую симметрию. Потенциальное поле носит локальный характер; поле в данной точке пространства зависит только от токов, существовавших в этой же точке. Электростатические поля следует рассматривать как предельный случай в формуле (1.69), соответствующий выключению токов, создавших статическое распределение заряда. Потенциальная энергия Для наших целей можно выра-одноатомного жидкого металла, зить линейные размеры свободного объема соотношением. Потенциальное поле, принимавшееся в предыдущих рассуждениях, изображено I на рис. 54, А, но вероятно, что ближе к действительности, особенно при высоких температурах, будет потенциальное поле, изображенное на рис. 54, В. Последняя кривая может рассматриваться как сочетание потенциальной кривой типа А с параболами, характеризующими гармонические осцилляторы. Потенциальное поле обладает следующими свойствами. Потенциальное поле, создаваемое взаимодействием электрона и протона, сферически симметрично относительно ядра, как начала координат. Потенциальное поле, создаваемое взаимодействием электрона и протона, сферически симметрично относительно ядра, как начала координат. Потенциальное поле, образуемое выходящими из заземлителя токовыми линиями, аналогично полю, которое было бы в вакууме вокруг заряженного электрода, имеющего размеры заземлителя. Потенциальное поле может быть в пространстве многих переменных. Потенциальное поле, создаваемое взаимодействием электрона и протона, сферически симметрично относительно ядра, как начала координат. Потенциальное поле, в котором движется электрон, определяется числом ядер ( или атомных остовов) и их взаимным расположением в пространстве, поэтому потенциальное поле в молекуле бензола иное, чем в молекуле нафталина или гексатриена. Таким образом, каждая молекула характеризуется своим гамильтонианом. В заданном потенциальном поле возможны только определенные стационарные молекулярные орбиты для электрона, характеризующиеся дискретными значениями энергии. Решение уравнения Шредингера ( 1) для заданного потенциального поля в принципе позволяет найти молекулярные орбиты и энергию электрона на этих орбитах. Точное решение уравнения Шредингера представляет очень трудную задачу. Однако имеется большой круг вопросов, интересующих химика, на который можно получить ответ путем приближенного решения уравнения Шредингера. Потенциальное поле в таком случае имеет симметрию Од ( см. трактовку молекулы C3v стр. Последняя имеет те же типы симметрии, что и точечная группа Та ( Alt A. Потенциальное поле, в котором движется электрон, определяется числом ядер ( или атомных остовов) и их взаимным расположением в пространстве, поэтому потенциальное поле в молекуле бензола иное, чем в молекуле нафталина или гексатриена. Таким образом, каждая молекула характеризуется своим гамильтонианом. В заданном потенциальном поле возможны только определенные стационарные молекулярные орбиты для электрона, характеризующиеся дискретными значениями энергии. Решение уравнения Шредингера ( 1) для заданного потенциального поля в принципе позволяет найти молекулярные орбиты и энергию электрона па этих орбитах. Точное решение уравнения Шредингера представляет очень трудную задачу. Однако имеется большой круг вопросов, интересующих химика, на который можно получить ответ путем приближенного решения уравнения Шредингера. Потенциальное поле - векторное поле, в котором криволинейный интеграл зависит не от формы пути, а только от начальной и конечной точек пути. Электродная система и потенциальное поле ЧОК, СХОДЯЩИЙСЯ вблизи электронной пушки ( а и ее оптическая аналогия ( 6. катода. Место наименьшего сечения, пучка носит название области скрещения. Иммерсионная линза должна быть настроена таким образом, чтобы на экране S получилось действительное изображение области скрещения О, а не соответствующего участка катода. Этим достигается существенное уменьшение размера пятна на экране. Потенциальное поле и электронные тра - ЛИТЬ фокусировку Вблизи еКТ РИИ вбЛИЗИ Катода электронной пушки. Потенциальное поле - поле ( например, электрическое), работа сил которого зависит только от положения начальной и конечной точек пути, по которому происходит перемещение точки приложения сил этого поля ( например, перемещение электрического заряда), но не зависит от пути, по которому происходит перемещение. Потенциальное поле - поле ( например, электрическое), работа сил которого зависит только от положения начальной и конечной точек пути, по которому происходит перемещение точки приложения сил этого поля ( например, перемещение электрического заряда), но не зависит от пути, по - которому происходит перемещение. Потенциальное поле является одним из наиболее простых векторных полей, ибо оно полностью определяется одной скалярной функцией / ( М) - потенциалом, в то время как произвольное векторное поле F ( M) определяется тремя скалярными функциями - проекциями Fx, F y, Fz. В дальнейшем будем предполагать, что поле F непрерывно дифференцируемо в рассматриваемой области. Потенциальное поле обладает следующими свойствами. Потенциальное поле называют также безвихревым полем. Такое потенциальное поле характеризуется тем, что для него возможными являются только те решения уравнения Шредингера [1,2], при которых энергия Е имеет значения, заполняющие ряд дискретных полос или зон. Это обусловлено тем, что для других значений Е, не лежащих в этих зонах, волновое число k электрона становится мнимым и, следовательно, эти значения Е запрещены. Значения k, при которых имеют место разрывы непрерывности Е, лежат в - пространстве [2] на поверхности многогранника, называемого зоной Бриллюэна. Электрон с энергией, меньшей Ег, будет находиться в первой зоне Бриллюэна. У щелочных металлов первая зона содержит 2УУ - состояний, где N - число валентных электронов в кристалле, так что первая зона заполнена лишь наполовину. Если в первой зоне имеются незаполненные энергетические состояния, то соответствующие вещества должны быть хорошими электронными проводниками. Температурная зависимость ионизационного потенциала. Поскольку потенциальное поле над поверхностью подложки отражает ее симметрию, то металлические атомы располагаются закономерно, и образующиеся зародыши имеют определенную ориентацию. Если потенциальное поле обладает сферической симметрией, как это имеет место в рассматриваемой задаче, уравнение Шредингера проще решать в сферических, а не в декартовых координатах. На рис. 3.1 показаны сферические координаты: г - расстояние до электрона от протона; 9 - угол, образуемый г с осью z; ф - угол, который образует с осью х проекция вектора г на плоскость ху. Если потенциальное поле не меняется во времени, 4 ( x, у, z, t) y ( x, у, z) e - i ( 2 IH) Et, Временное уравнение служит для описания процессов во времени. Если потенциальное поле обладает сферической симметрией, как это имеет место в рассматриваемой задаче ( V - е2 / / -), уравнение Шредингера выгоднее решать в сферических, а не в декартовых координатах. Поскольку любое потенциальное поле может быть смоделировано непрерывной проводящей средой, такую проводящую модель, очевидно, можно заменить эквивалентной электрической схемой, состоящей из совокупности дискретных электрических сопротивлений. Рассмотрим потенциальное поле сил, с которым приходится иметь дело при статическом расчете упругих систем. К расчету шагового напряжения [ IMAGE ] Эквипотенциальная по. Рассмотрим потенциальное поле вокруг цилиндрического за-землителя небольшого диаметра длиной IE, лежащего на глу - бине hE параллельно поверхности земли. Началом системы координат является точка на поверхности земли, из которой опущен перпендикуляр в центр заземлителя. Для потенциального поля rotvn - О, т.е. линии этого поля незамкнуты. Циркуляция потенциального поля по любому контуру равна нулю. Примером потенциального поля служит поле сил тяготения. Примером потенциального поля может служить электростатическое поле Е ( см. гл. Вектор потенциального поля является градиентом некоторой скалярной функции. Изучение потенциального поля значительно облегчается тем, что это поле вполне определяется заданием одной скалярной функции - его потенциала. Для потенциального поля понятия напряжение между точками Л и Б и разность потенциалов в точках А и В, по существу, совпадают. В потенциальном поле положительные заряды всегда стремятся двигаться от точек более высокого потенциала к точкам более низкого, в результате чего все потенциалы выравниваются; заряды разных знаков стремятся к сближению под действием силы их взаимного притяжения, к взаимному компенсированию один другого; в итоге все электрические эффекты исчезают. Поэтому для работы электротехнических устройств совершенно необходимо существование каких-то процессов, в которых отрицательные заряды удаляются от положительных вопреки закону Кулона. В потенциальном поле циркуляция по любому контуру равна нулю. При этом предполагается, что контур L можно заключить в односвязную область, во всех точках которой функции Ах, Ач, Аг и их производные непрерывны. В потенциальных полях работа на любом замкнутом контуре равна нулю. В потенциальном поле при перемещении частицы из различных точек В; в фиксированную точку О совершается работа, которая зависит только от радиусов-векторов Г; точек В. Функция U ( r), зависящая только от г и определяющая работу по перемещению частицы в потенциальном поле, называется потенциальной энергией этой частицы в данном поле. Потенциальная энергия определяется с точностью до постоянной величины. Работа сил в потенциальном поле равна разности потенциальных энергий в начальном и конечном положениях частицы. В потенциальном поле линейный интеграл ( работа) не зависит от формы линии, соединяющей какие-либо две его точки, а циркуляция всегда равна нулю. В потенциальном поле циркуляция по любому замкнутому контуру равна нулю. В потенциальном поле циркуляция по любому контуру равна нулю. При этом предполагается, что контур L можно заключить в односвязную область, во всех точках которой функции Ах, А, Аг и их производные непрерывны. В безвихревом потенциальном поле максимальное и минимальное значения функции внутри области не могут превосходить максимального и минимального значений функции на границах области. Поэтому при расчете на ЭВМ бывает удобно принять минимальный потенциал на границе области за 1Гулевой уровень и всем узловым точкам внутри области задать нулевые значения. Этот прием экономит время при составлении программы, а увеличение времени машинного счета, из-за необходимости проведения нескольких лишних итераций, ничтожно. Потенциальную сетку следует накладывать на исследуемую область так, чтобы возможно большая часть линий, ограничивающих область, совпадала с узловыми точками потенциальной сетки. Если совпадения точек нет, то приходится заданный на границе потенциал экстраполировать в узловые точки сетки, ближайшие к границе, и считать потенциал этих точек в процессе итерации неизменным. Во внешнем потенциальном поле частица с массой т и зарядом е совершает одномерное гармоническое колебание с частотой со. К определению ротора вектора.| Структура магнитного поля прямолинейного тока. В потенциальном поле Agradp циркуляция вектора по любому замкнутому контуру L ( рис. 1 - 83) равна нулю. В идеально периодическом потенциальном поле электроны не рассеивались бы, тепловое равновесие не могло бы установиться и и было бы бесконечным. Однако в реальных кристаллах статические дефекты и решеточные колебания вызывают отклонения от периодичности.
Принцип суперпозиции |
|
|
|
Силы
в механике подчиняются принципу
суперпозиции (принципу независимости
действия сил): Если на материальное
тело действуют несколько сил, то
результирующую силу
Из второго закона Ньютона имеем:
где
Если
на материальную точку действует
несколько сил, то каждая из них сообщает
точке такое же ускорение, как если бы
других сил не было.
Найдем изменение импульса тела за
конечный промежуток времени
Δt = t2 – t1:
т.е., изменение импульса тела равно импульсу силы. В системе СИ семь основных единиц (см. приложение): метр (м), килограмм (кг), секунда (с), ампер (А), кельвин (К), кандела (кд), единица количества вещества (моль). Остальные единицы называются производными и получаются из физических законов, связывающих их с основными единицами. Например из второго закона Ньютона производная единица силы получается равной 1 кг·м/с2, что соответствует 1Н. |
22. Неинерциа́льная систе́ма отсчёта — система отсчёта, к которой не применим закон инерции (говорящий о том, что каждое тело, в отсутствие действующих на него сил, движется по прямой и с постоянной скоростью), и поэтому для согласования сил и ускорений в которой приходится вводить фиктивные силы инерции. Всякая система отсчета, движущаяся с ускорением относительно инерциальной, является неинерциальной.
Законы Ньютона выполняются только в инерциальных системах отсчёта. Для того, чтобы найти уравнение движения в неинерциальной системе отсчёта, нужно знать законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной.
Классическая механика постулирует следующие два принципа:
время абсолютно, то есть промежутки времени между любыми двумя событиями одинаковы во всех произвольно движущихся системах отсчёта;
пространство абсолютно, то есть расстояние между двумя любыми материальными точками одинаково во всех произвольно движущихся системах отсчёта.
Эти два принципа позволяют записывать уравнение движения материальной точки относительно любой неинерциальной системы отсчёта, в которой не выполняется первый закон Ньютона.
Основное уравнение динамики относительного движения материальной точки имеет вид:
![]() ,
,
где ![]() — масса тела,
— масса тела, ![]() —
ускорение тела относительно неинерциальной
системы отсчёта,
—
ускорение тела относительно неинерциальной
системы отсчёта, ![]() —
сумма всех внешних сил, действующих на
тело,
—
сумма всех внешних сил, действующих на
тело, ![]() — переносное
ускорение тела,
— переносное
ускорение тела, ![]() — кориолисово
ускорение тела.
— кориолисово
ускорение тела.
Это уравнение может быть записано в привычной форме Второго закона Ньютона, если ввести фиктивные силы инерции:
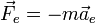 —
переносная
сила инерции
—
переносная
сила инерции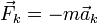 — сила
Кориолиса
— сила
Кориолиса
II закон Ньютона в неинерциальных системах отсчёта.
Если на тело действуют силы, то результирующая этих сил вызывает ускорение пропорциональное этой силе и обратно пропорционально массе.
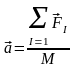 ;
в инерциальной системе отсчёта.
;
в инерциальной системе отсчёта.
Но существуют системы отсчёта, в которых наблюдается ускоренное движение тел без воздействия на них каких – либо тел.

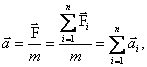
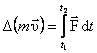 ,
,